The double-stage delay-multiply-and-sum image reconstruction method improves imaging quality in a LED-based photoacoustic array scanner

Abstract

Light-emitting diode-based photoacoustic imaging is more compact and affordable than laser-based systems, but it has low power and hence a high number of replicates. Here, we describe double-stage delay-multiply-and-sum (DS-DMAS) to improve image quality collected on a LED-based scanner. DS-DMAS was evaluated experimentally using point targets (in different laterals and depths) as well as a hair and a rabbit eye. This algorithm can compensate for the low SNR of LED-based systems and offer better lateral resolution of about 60%, 25%, higher contrast ratio of about 97%, 34%, and better full-width-half-maximum of about 60%, 25%, versus delay-and-sum) and delay-multiply-and-sum, respectively. More importantly, DS-DMAS offers this using a smaller number of frames (only 2% of all the frames). These results indicate that DS-DMAS might be a valuable tool in the translation of LED-based and other low power PAI systems.

1. Introduction

Photoacoustic imaging (PAI) is an emerging biomedical imaging modality also known as optoacoustic imaging. PAI uses the resolution of the ultrasound imaging and the contrast of the pure optical imaging to provide structural, molecular, and functional information [[1], [2], [3], [4], [5]]. In PAI, a short laser pulse irradiates a target/sample resulting in a spatially-confined temperature rise. Photoacoustic waves are generated as a result of the thermoelastic expansion effects [[6], [7], [8], [9]]. Wideband ultrasound transducers are used to record the photoacoustic waves. Finally, an optical absorption distribution map (image) of the target/tissue can be obtained using mathematical processing of this data [[10], [11], [12], [13], [14], [15]]. PAI has been used in tumor detection [16,17], cancer detection and staging [18,19], ocular imaging [20,21], monitoring oxygenation in blood vessels [22,23], molecular imaging [24], functional imaging [25,8,26], oncology [27,28], ophthalmology [29], cardiology [30], etc.

High energy Nd:YAG lasers are most commonly used in PAI systems but they are expensive and bulky [[31], [32], [33]]. To address these problems, pulse laser diodes and light emitting diodes (LEDs) have been used in PAI imaging systems and are most commonly used with linear-array transducers [[34], [35], [36], [37], [38]]. While LEDs are inexpensive, compact, and multi-wavelength, they have a low power and usually provide a low signal-to-noise (SNR) [38]. Having a low SNR can lead to a noisy photoacoustic image or longer scan times to collect multiple averages and optimize SNR.

Signal processing algorithms can improve SNR in phoatoacoustic data. The most common beamforming algorithm in linear-array PAI is delay-and-sum (DAS). It is simple, but it also produces low quality (resolution and contrast) images due to its blindness (considering all the detected signals the same) [39,40]. Delay-multiply and Sum (DMAS) can address the problems of DAS for linear-array PAI [41,42] but still suffers from low contrast when noise is present in the dataset. In fact, the cross correlation process of DMAS would not be able to reduce a high level of noise. Delay-and-standard-deviation (DASD) facilitates the detection of interventional devices for some special applications such as needle biopsy or cardiac catheterization [43]. DMAS provides a low resolution compared to algorithms such as minimum variance (MV) [44,45]. This problem has been addressed in [46] for PAI using the combination of minimum variance and DMAS. The DMAS is combined with eigenspace minimum variance beamformer to reduce the effects of off-axis signals in reconstructed images while the resolution is retained [47]. A sparsity-based minumum variance is proposed to improve the contrast of photoacoustic images, retaining the significant full-width-half-maximum of minimum variance [45]. A nonlinear algorithm is also introduced for photoacoustic image formation in [14]. This algorithm imposes a low computational complexity to PAI system.

To address this problem, we recently introduced Double Stage-DMAS (DS-DMAS) and showed that it offers higher contrast than DMAS [48,49]. Here, for the first time, we combine the advances of DS-DMAS with advances in LED-based PAI and showed that DS-DMAS addresses the low SNR inherent to the LED-based excitation. This approach was validated with point targets, hair, and in vivo experiments. This method offers high contrast and requires a lower number of frames. DS-DMAS improves the temporal/spatial (lateral and axial) resolution, contrast ratio, and reduces level of sidelobes.

2. Materials and methods

2.1. Image formation

After a laser excitation, photoacoustic waves are generated as a result of the thermoelastic expansion effect. Linear-array transducers detect the propagated photoacoustic waves. Finally, using mathematics, we can form photoacoustic images that represent an optical absorption distribution map of the target. DAS, as the most commonly used algorithm, is as follows:

$$y_{\mathrm{DAS}}(k)=\sum _{i=1}^M{x}_i(k-{\mathrm{\Delta }}_i),$$ (1)

where y_DAS(k) is the output of beamformer, k is time index, M is the number of array elements, and x_i(k) and Δ_i are detected signals and corresponding time delay for detector i, respectively [44,50]. The DAS algorithm is simple to implement and can be used for real-time imaging. This is why it is the most prevalent algorithm used in photoacoustic/ultrasound imaging systems. However, DAS leads to low quality images having a low resolution and high level of sidelobes due to its non-adaptiveness. One of the algorithm introduced to address the incapabilities of DAS is DMAS which can be written as follows [51]:

$$y_{\mathrm{DMAS}}(k)=\sum _{i=1}^{M-1}\sum _{j=i+1}^M{x}_i(k-{\mathrm{\Delta }}_i)x_j(k-{\mathrm{\Delta }}_j),$$ (2)

To overcome the dimensionally squared problem of (2), followings are suggested in [51]:

$${\hat{x}}_{\mathrm{ij}}(k)=\mathrm{sign}[x_i(k-{\mathrm{\Delta }}_i)x_j(k-{\mathrm{\Delta }}_j)]\sqrt{|x_i(k-{\mathrm{\Delta }}_i)x_j(k-{\mathrm{\Delta }}_j)|},\mathrm{for}1⩽i⩽j⩽M.$$ (3)

$$y_{\mathrm{DMAS}-C}(k)=\sum _{i=1}^{M-1}\sum _{j=i+1}^M{\hat{x}}_{\mathrm{ij}}(k).$$ (4)

The DMAS is a non-linear algorithm and uses a correlation process to form a high contrast photoacoustic image [41,42]. However, as shown in previous studies [48,49,46] and in the following section, the performance of DMAS is degraded at the presence of high level of imaging noise since its correlation process does not work well when there were high levels of noise affecting the imaging system. DMAS also has relatively low resolution advantages versus MV [44,46]. One of the alternatives to address the degraded performance of the DMAS is DS-DMAS [48,49], which mathematically expands DMAS (presented in (2)):

$$\begin{array}{cc}{y}_{\mathrm{DMAS}}(k)=\hfill & \sum _{i=1}^{M-1}\sum _{j=i+1}^M{x}_{\mathrm{id}}(k)x_{\mathrm{jd}}(k)=\hfill \\ \hfill & \underset{\mathrm{first}\mathrm{term}}{\underbrace{[x_{1d}(k)x_{2d}(k)+x_{1d}(k)x_{3d}(k)+\cdots +x_{1d}(k)x_{\mathrm{Md}}(k))]}}\hfill \\ \hfill & +\underset{\mathrm{second}\mathrm{term}}{\underbrace{[x_{2d}(k)x_{3d}(k)+x_{2d}(k)x_{4d}(k)+\cdots +x_{2d}(k)x_{\mathrm{Md}}(k)]}}\hfill \\ \hfill & +\cdots \hfill \\ \hfill & +\underset{(\mathrm{M}-2)\mathrm{th}\mathrm{term}}{\underbrace{[x_{(M-2)d}(k)x_{(M-1)d}(k)+x_{(M-2)d}(k)x_{\mathrm{Md}}(k)]}}\hfill \\ \hfill & +\underset{(\mathrm{M}-1)\mathrm{th}\mathrm{term}}{\underbrace{[x_{(M-1)d}(k)x_{\mathrm{Md}}(k)]}}.\hfill \end{array}$$ (5)

where x_id(k) and x_jd(k) are delayed detected signals for element i and j (x_i(k − Δ_i) and x_j(k − Δ_j)), respectively. The source of the low resolution and performance of DMAS, at the presence of high level of imaging noise and noisy media, is the annotated terms in (5). All entries of the terms in (5) are delayed, and there are summation operations between the terms. Thus, we have DAS inside the expansion of DMAS. As stated in [48,49], another stage of correlation process inside the DMAS can suppress noise and artifacts unmitigated by the DMAS. The formula of DS-DMAS can then be written as follows:

$$y_{\mathrm{DS}-\mathrm{DMAS}}(k)=\sum _{i=1}^{M-2}\sum _{j=i+1}^{M-1}{x}_{\mathrm{it}}(k)x_{\mathrm{jt}}(k),$$ (6)

where x_it and x_jt are the ith and jth term shown in (5). Below, we evaluated the performance of the DS-DMAS algorithm for LED-based PAI system. We have used Matlab R2017b for all of our processing. This PAI system (clarified in Section 2.2) saves the photoacoustic signal in Matlab after 640 excitation pulses. Therefore, in this paper, a single frame of photoacoustic data is generated as a result of 640 excitation pulses. The squared problem of DMAS algorithm (as a result of one stage of correlation) is addressed using the methods presented in Sections (3) and (4). In other words, we have used the same method in DS-DMAS to prevent the image voxel intensities to have the power of four. The squared root results from the multiplications inside the DS-DMAS algorithm. Before each correlation process, we use methods presented in Sections (3) and (4) in order to change the dimension of the calculated samples. In this way, the dimension of the image generated by DS-DMAS will be volt, not volt to the power of four. All the beamformed data are first normalized and then, log compressed. Finally, after applying dynamic range, we use another normalization to better present the reconstructed images.

2.2. Experimental setup

All the experiments in this study are performed using a commercial available LED-based PAI system from PreXion Corporation (Tokyo, Japan) described previously [38]. The LED-based scanner has been described previously [38,34]. High density, high power LED are utilized as illumination source. Two LED arrays include 4 rows of 36 single embedded LEDs attached to either side of an ultrasound transducer. They are the optical and acoustic path of our LED-based photoacoustic imaging system. The LED-based imaging system used the following optical excitation parameters: 690 nm, 4 KHz repetition rate, and 100 ns pulse width. A 128-element linear array transducer with a central frequency of 10 MHz and bandwidth of 80.9% was used to detect the photoacoustic signal. The data acquisition unit has a dynamic range of 16 bits with 1024 sample for each element. The sampling rates of the photoacoustic and ultrasound modalities are 40 MHz and 20 MHz, respectively.

2.2.1. Spatial resolution measurement

In order to evaluate the lateral resolution, we printed parallel lines (150 μm wide) with various distances (778, 575, and 520 μm) on transparent film. The samples are fixed between two layers of 1% agar placed in water tank. We used bright field microscopy imaging system (Life Technologies Inc., Ca, USA) to measure the accurate spacing between lines. We utilized a black human hair with diameter of 90 μm to evaluate the axial resolution of the LED-based imaging system using DAS, DMAS, and DS-DMAS as the reconstruction algorithms. The human hair was embedded between layers of 1% agar, and B-mode photoacoustic images were acquired. The LED repetition rate and B-mode frame rate were 4 KHz and 6 Hz, respectively.

2.2.2. Depth measurement

Methylene blue (MB) (Fisher Science Education Inc., PA, USA) were purchased and dissolved in deionized water. We used 50 μm MB as exogenous contrast agent at different depths with interval distance of 0.5 mm. The MB is placed inside Teflon light wall tubes (Component Supply Company, FL, USA). The samples are scanned at different depths from 16 mm to 24 mm. 2% intralipid (20%, emulsion, Sigma–Aldrich Co, MO, USA) mixed with agar is used as the scattering media in this experiment. The LED repetition rate and B-mode frame rate are 4 KHz and 3 Hz, respectively.

2.2.3. In vivo experiment

New Zealand white rabbits (∼5 kg) were used for in vivo evaluation of the proposed method in this study. The animal experiment was performed in compliance with the Institutional Animal Care and Use Committee established by University of California San Diego. Intramuscular injection of ketamine (35 mg/kg) and xylazine (5 mg/kg) was used to anesthetize the animal. The pupils were dilated and anesthetized using 2.5% phenylephrine hydrochloride, 0.5% proparacaine hydrochloride, and 1% tropicamide. The heart rate, peripheral capillary oxygen saturation, respiration rate, and temperature were monitored during the experiment. The animal was placed on a recirculating water blanket kept at 39 °C. An ocular speculum held the eye open, and ultrasound gel coupled the eye to the transducer. A wavelength of 690 nm is used as the excitation source. The LED repetition rate and B-mode frame rate for in vivo experiments are the same as those used in Section 2.2. The maximum permissible exposure (MPE) from the American National Standard Institute (ANSI) for 690 nm light with 10 s illumination is ∼5 mJ/cm² [52]. The LED source used 5.5 μJ/cm² which is much lower than the ANSI limit. We used ten-second illumination for averaging purpose. The DAS, DMAS, and DS-DMAS were again utilized as reconstruction algorithms.

3. Results and discussion

3.1. Spatial resolution assessment

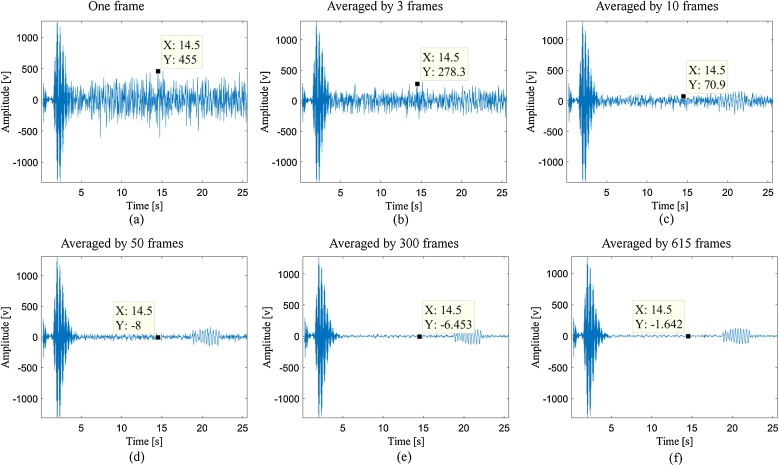
LED systems have lower power than laser-based systems [38]; thus, we used averaging to improve the signal-to-noise (SNR) of the received photoacoustic signals. SNR is defined as the ratio of signal power to the noise power, often expressed in decibels. To illustrate this, consider Fig. 1 where the averaging was applied on different number of frames. By comparing Fig. 1(a) and Fig. 1(c), it can be seen that having an average of 10 frames would suppress the imaging noise amplitude (about 384 V), which finally results in a higher SNR.

Fig. 1.

(a) A single line of detected photoacoustic signal (one frame). Photoacoustic signals averaged by (b) 3 frames, (c) 10 frames, (d) 50 frames, (e) 100 frames, (f) 300 frames and (g) 615 frames. The cursors show the amplitude of the noisy part of the detected signals indicating that a higher SNR would be achieved using a higher number of frames in averaging procedure.

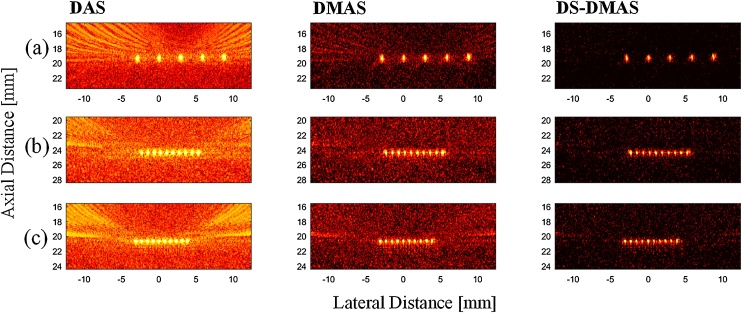
The reconstructed photoacoustic images using the data generated by the point-target phantom are shown in Fig. 2. The DAS, DMAS and DS-DMAS are used for reconstruction of the first, second, and third column of the images where the distance between the points are decreased from (a) to (g), as clarified in Section 2.2.1. The performance of the DS-DMAS algorithm, in terms of noise suppression and target separability, can also be evaluated using these images. As can be seen in Fig. 2, even though DMAS degrades the imaging noise and artifacts, compared to DAS, the image contrast and resolution is still affected by the off-axis signals and noise. DS-DMAS further suppresses the artifacts and results in a higher quality image (the background noise of the photoacoustic images is better suppressed (darker background)), compared to DAS and DMAS. This results in higher contrast and thus a better ability to identify targets.

Fig. 2.

Reconstructed photoacoustic images using the point-target phantom. DAS, DMAS, and DS-DMAS were used for the first, second, and third columns, receptively. The distance between the targets is decreased where it is (a) 778 μm, (b) 575 μm and (c) 520 μm, respectively. All the images are shown with a dynamic range of 60 dB. 10 frames of the detected photoacoustic signals were used to have a higher SNR. Considering images shown in (b), DS-DMAS degrades the sidelobes about 39 dB and 20 dB, compared to DAS and DMAS, respectively, which results in a darker background (better noise suppression).

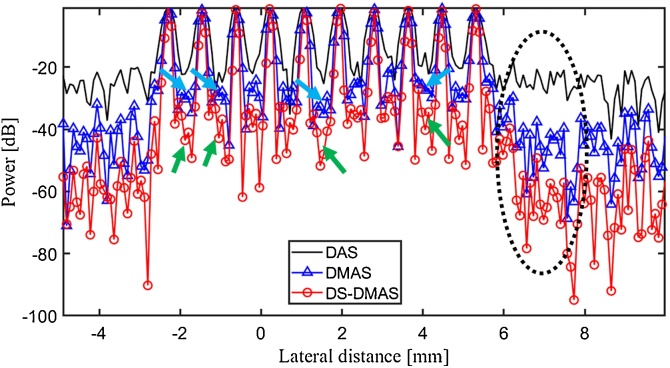
To quantitatively evaluate the algorithms, Fig. 3 presents the lateral variations of the images shown in Fig. 2(b). As demonstrated in Fig. 3, the lateral valleys (background signal) of the DS-DMAS are almost 17 dB and 8 dB lower than DAS and DMAS (see the arrows), respectively, indicating the better target separability of DS-DMAS. In addition, DS-DMAS leads to lower sidelobes in comparison with DAS and DMAS (see the circle) where DAS, DMAS and DS-DMAS result in the sidelobes of about −28 dB, −47 dB, and −67 dB, respectively. Thus, DS-DMAS degrades the sidelobes by about 39 dB and 20 dB, compared to DAS and DMAS, respectively.

Fig. 3.

The lateral variations of the images shown in Fig. 2(b). Arrows can be used to compare the lateral valleys obtained by DMAS and DS-DMAS (8 dB lower than DMAS). The dotted-circle shows the lower sidelobes of DS-DMAS (about 39 dB and 20 dB, compared to DAS and DMAS, respectively).

Next, we calculated the full-width-half-maximum (FWHM) in −6 dB to quantitatively evaluate the resolution gained by the reconstruction methods. FWHM is an expression of the lateral distance given by the difference between the two extreme values of the lateral variation at which the amplitude value is equal to half of its maximum value (−3 dB less than its maximum power). For better evaluation, we are considering −6 dB less than the maximum power. DAS, DMAS, and DS-DMAS lead to a FWHM of about 0.37 mm, 0.20 mm, and 0.15 mm, respectively. Thus, DS-DMAS leads to a narrower mainlobe width (better resolution), compared to other methods.

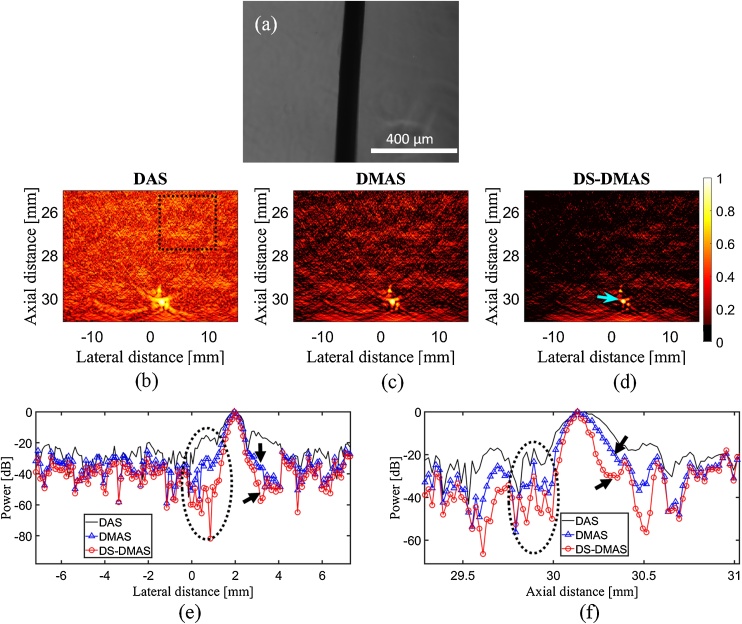
As mentioned in Section 2.2.1, we have also used a hair as the target of imaging. The microscopy image of the hair is presented in Fig. 4(a). The reconstructed photoacoustic images using the data generated by the hair are shown in Fig. 4(b–d). As seen, the DS-DMAS better suppresses the noise and artifacts. To have a better evaluation, consider the lateral/axial variations shown in Fig. 4(e) and (f). The sidelobes obtained by DS-DMAS (see the levels indicated by the circles and arrows in Fig. 4(e)) are almost −38 dB and −23 dB lower than DAS and DMAS, respectively. The rangelobes (see Fig. 4(f)) generated by DS-DMAS is about 23 dB and 9 dB lower than DAS and DMAS, respectively. The levels of sidelobes and rangelobes prove the higher performance of the proposed method. Indeed, DS-DMAS results in higher contrast because the two stages of correlation process suppresses the background noise and sidelobes while the imaging target is detectable and unmitigated (peak level of the lateral variations of DS-DMAS is the same as DAS.

Fig. 4.

(a) The microscopy image of the hair. Reconstructed photoacoustic images using the data generated by the hair and (b) DAS, (c) DMAS, and (d) DS-DMAS algorithms. All images are shown with a dynamic range of 40 dB (for better evaluation). 100 frames of the detected photoacoustic signals were used to have a higher SNR. The arrow shows the target of imaging. The dashed square shows the region we used for contrast evaluation. DS-DMAS suppresses the sidelobes about −38 dB and −23 dB, in comparison with DAS and DMAS, respectively. (e) and (f) are the lateral and axial variations of the images, respectively. The arrows and circle show the level of sidelobes where the superiority of DS-DMAS is proved.

We have also used contrast ratio (CR) metric for evaluation:

$$\mathrm{CR}=20{log}_{10}\left(\frac{{\mu }_{\mathrm{background}}}{{\mu }_{\mathrm{foreground}}}\right)$$ (7)

where μ_background and μ_foreground are the mean of image intensity before log compression inside the dotted-square (shown in Fig. 5(f)) and the maximum intensity of the image, respectively. It should be mentioned that CR is usually used for cyst targets where μ_background and μ_foreground are concerned with a region inside and outside of a cyst, respectively [49]. However, here, we have used this metric to evaluate the images obtained with point targets. The higher the absolute of CR, the higher performance of an algorithm would be. We have measured the CR using the pixels inside the dotted-square region shown in Fig. 4(a). The DAS, DMAS, and DS-DMAS lead to a CR of about −23.89 dB, −35.10 dB, and −47.41 dB, respectively, indicating a higher contrast obtained by DS-DMAS. The axial resolution (axial FWHM in −6 dB) for DAS, DMAS, and DS-DMAS is about 0.23 mm, 0.18 mm, and 0.14 mm, respectively. In addition, the lateral resolution (lateral FWHM in −6 dB) of DAS, DMAS, and DS-DMAS is about 1.01 mm, 0.71 mm, and 0.64 mm, respectively. Thus, in both axes, we have resolution improvement using DS-DMAS (0.04 mm and 0.07 mm for axial and lateral resolution, respectively, compared to DMAS).

Fig. 5.

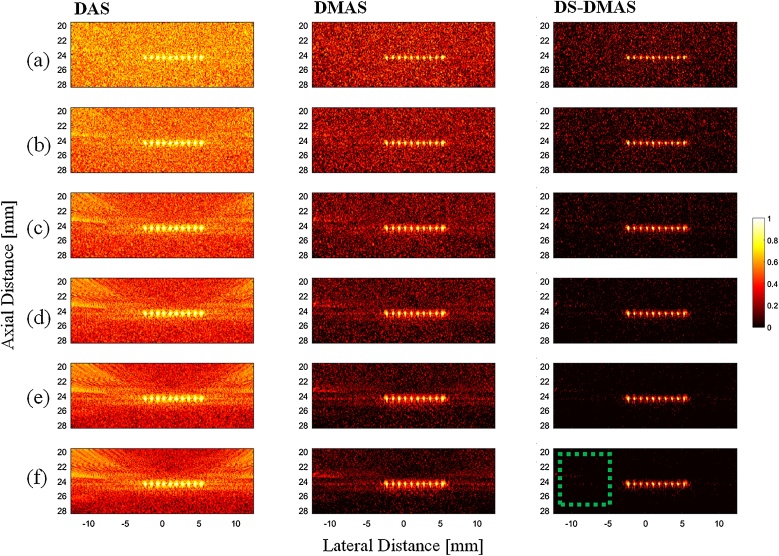
Reconstructed photoacoustic images using the point-target phantom. DAS, DMAS, and DS-DMAS were used for the first, second, and third columns of the images, respectively. All images are shown with a dynamic range of 60 dB. (a) 1 frame, (b) 3 frames, (c) 10 frames, (d) 20 frames, (e) 50 frames, and (f) 100 frames of the detected photoacoustic signals were used for averaging. The background noise is suppressed (darker background) using a higher number of frames. The dotted-square is used for CR calculation.

3.1.1. Temporal resolution assessment

Next, we studied the effect of frame number on the reconstructed images. The photoacoustic images are presented in Fig. 5 using different number of frames. More frames minimizes the effects of noise and leads to higher image quality (compare Fig. 5(a) with Fig. 5(f)). However, this also leads to longer scan times. It should be noticed that the image gained by one frame of data and DS-DMAS has a higher quality (higher contrast and better resolution) compared to the one gained by 100 frames and DAS. This shows the superiority of the proposed method.

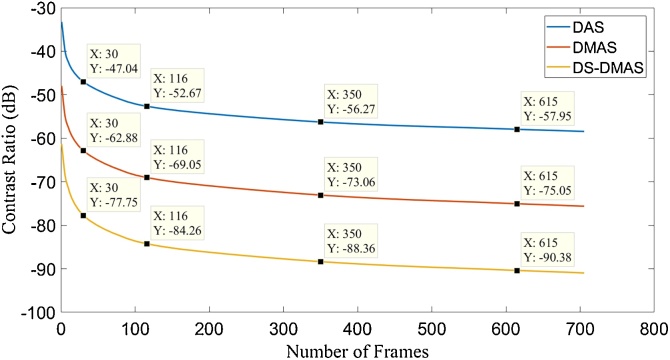
Fig. 6 shows the obtained CR per number of frames for all the beamformers. With 350 frames, DS-DMAS results in CR improvement of about 32 dB and 15 dB versus DAS and DMAS, respectively.

Fig. 6.

CR for different number of frames used in averaging and beamforming methods. The data related to Fig. 5 was used. The cursors show the CR levels per a number of frames.

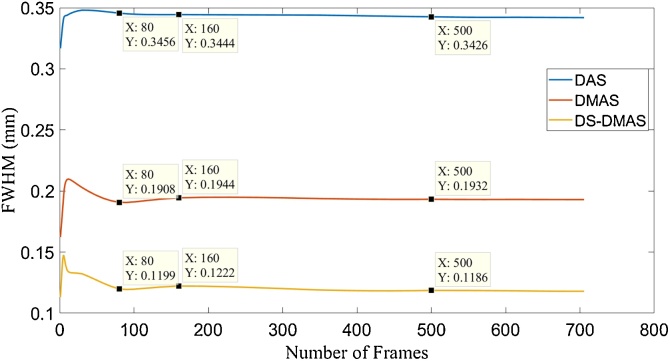
We have also calculated the FWHM (in −6 dB) per number of frames, for all the beamformers. The results are presented in Fig. 7. At the low number of frames, it can be seen that the FWHM metric is highly incremental using all the beamformers, which is undesired. This is because for the frame numbers before the peaks of the graphs, the point targets are not completely detected by the beamformers. As can be see in Fig. 7, DS-DMAS results in a lower FWHM in all the frame numbers. With a frame number of 160, DS-DMAS reduced the FWHM about 0.22 mm and 0.07 mm versus DAS and DMAS, respectively.

Fig. 7.

FWHM (in −6 dB) for different number of frames used in averaging and beamforming methods. The data related to Fig. 5 was used. The cursors show the FWHM per a number of frames.

3.2. Penetration depth evaluation

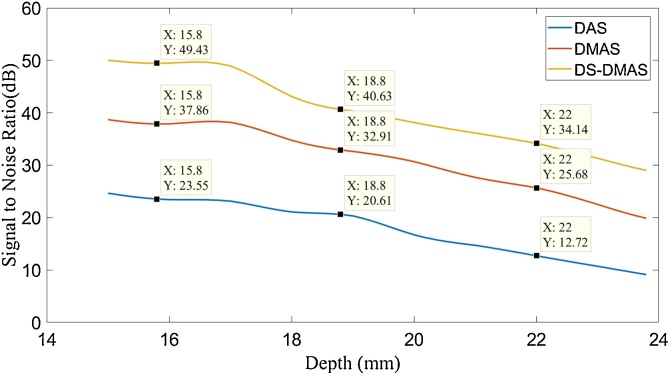
We have evaluated the performance of DS-DMAS algorithm using point-targets positioned at different depths, inside a scatter media. We have calculated the SNR of the images obtained with the algorithms. SNRs are calculated using the formula mentioned in [46]. Fig. 8 shows the calculated SNRs. Curve fitting is used for better presentation of the measurements. As can be seen, DS-DMAS outperforms other methods. Consider, for example, the depth of 22 mm, where DS-DMAS improves the SNR of about 22 dB and 9 dB compared to DAS and DMAS, respectively.

Fig. 8.

SNR at different depths of imaging. 1500 frames were used in signal averaging. The data related to the depth experiment was used. The cursors show the SNR levels per depth.

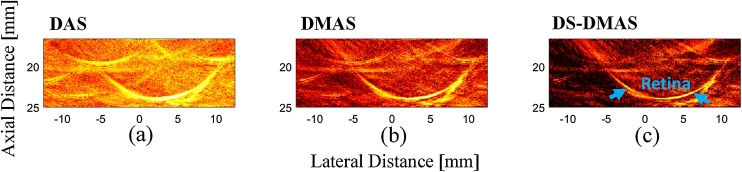
3.3. In vivo experiment

Finally, we evaluated the utility of DS-DMAS with in vivo data. We and others [20,21,53,54] have previously imaged the retina with photoacoustic imaging, and use it as an example here. The reconstructed images obtained by the algorithms are shown in Fig. 9. The retina of the rabbit can be clearly seen in Fig. 9(c); data highlighted via the arrows. Again, the background noise and artifacts of the image reconstructed by DS-DMAS are lower than that of DAS and DMAS. The background noise is about −29 dB, −40 dB, and −47 dB, for DAS, DMAS and DS-DMAS, respectively, proving the ability of DS-DMAS to suppress noise in vivo (by 18 dB and 7 dB, compared to DAS and DMAS, respectively). Future work will implement DS-DMAS on a GPU to reduce the computational time for near real-time imaging [55].

Fig. 9.

Reconstructed photoacoustic images using the data generated by the in vivo experiment. (a) DAS, (b) DMAS, and (c) DS-DMAS. All images are shown with a dynamic range of 60 dB (for better evaluation). The 1536 frames of the detected photoacoustic signals have a higher SNR. The arrow shows the location of the retina. The background noise of the DS-DMAS is lower than DAS and DMAS (18 dB and 7 dB, respectively).

4. Conclusion

In this paper, we showed that the DS-DMAS algorithm can compensate for the low SNR of LED-based PAI systems. The proposed algorithm was compared to DAS and DMAS beamformers using experimental data generated by point targets, a human hair, and a rabbit retina. The DS-DMAS outperforms other algorithms in terms of FWHM in −6 dB (lateral and axial), level of sidelobes, CR, and lateral valleys. For instance, the proposed algorithm results in a higher CR of about −38 dB and −23 dB, compared to DAS and DMAS, using only 100 frames of the data generated by the hair (see Fig. 4). In addition, the CR provided by DS-DMAS using only one frame is about 5 dB higher than that of obtained with DAS having 1000 frames and 700 frames of the data generated by the hair and point target experiment (Fig. 6). The main improvement obtained by DS-DMAS would be a higher CR (lower sidelobes), which makes it an appropriate option for LED-based PAI systems.

Conflicts of interest

The authors declare that there is no conflict of interests regarding the publication of this paper.

Biographies

Moein Mozaffarzadeh received his BSc degree in electrical engineering from Babol Noshirvani University of Technology, Mazandaran, Iran, in 2015, and his MSc degree in biomedical engineering from Tarbiat Modares University, Tehran, Iran, in 2017. His current research interests include photoacoustic image reconstruction, ultrasound beamforming, and biomedical imaging system development. Currently, he is collaborating with different research groups in Tarbiat Modares University, Tehran University of Medical Sciences, University of California San Diego, Nanyang Technological University and Wayne State University.

Ali Hariri is a PhD student in the Nanoengineering Department at UCSD. He got his M.S. degree and B.S degree in Biomedical Engineering from Sharif University of Technology and Amirkabir University of Technology in Iran. He worked on developing different configurations of photoacoustic imaging technique including computed tomography and microscopy (both acoustic and optical resolution). He also worked on measuring the functional connectivity in resting state using fMRI images on methamphetamine dependence.

Colman Moore is a PhD student in the Nanoengineering department at UC San Diego. He graduated from the University of South Carolina Honors College with a B.S. in Biomedical Engineering. At USC he conducted research on nanoparticle drug delivery systems and Alzheimer's disease, and nanoparticle mobility at the Intl. Inst. for Nanotechnology at Northwestern University. He is currently studying the intersection of diagnostic and therapeutic nano-agents with biomedical imaging modalities.

Jesse Jokerst completed a B.S. cum laude at Truman State University. After a Ph.D. in Chemistry at UT Austin with John McDevitt, he completed a postdoc with Sam Gambhir in Stanford Radiology. Now an Assistant Professor in the Department of Nanoengineering at UC San Diego, the Jokerst group is eager to collaborate on projects broadly related to human health and nanotechnology.