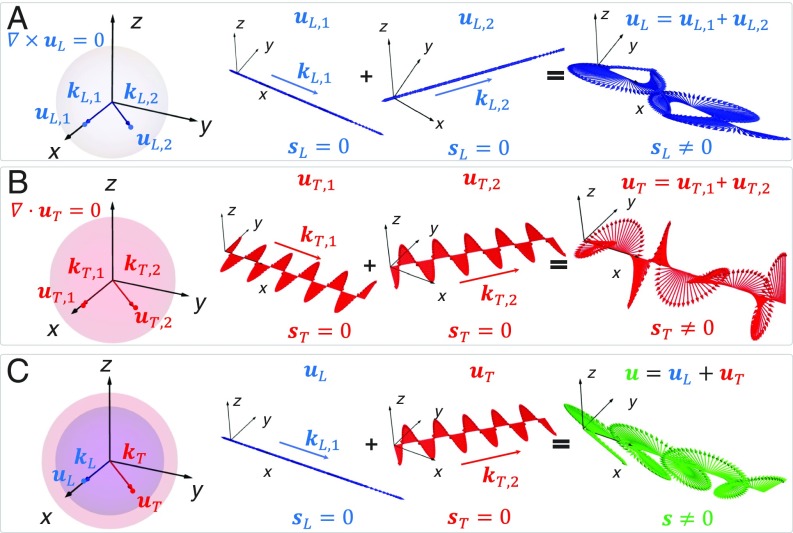
Fig. 1.
Geometry and spin of arbitrary waves. The strong relations between polarization profile and wave vector reflect the spin–orbit couplings: and , i.e., the spin–momentum lockings. (A) For the combinations of two longitudinal waves with different wave vectors , , the total elastic field carries nontrivial spin angular momentum density due to the wave interference, . (B) The transverse waves in the same settings, , also induce nontrivial spin density . (C) For the total elastic waves that contain longitudinal and transverse plane waves simultaneously, , the total elastic spin density is attributed to the hybrid spin density , which reflects the major geometrical difference between longitudinal and transverse waves. The spheres in the figure are spheres, and the real parts of displacement fields are plotted.