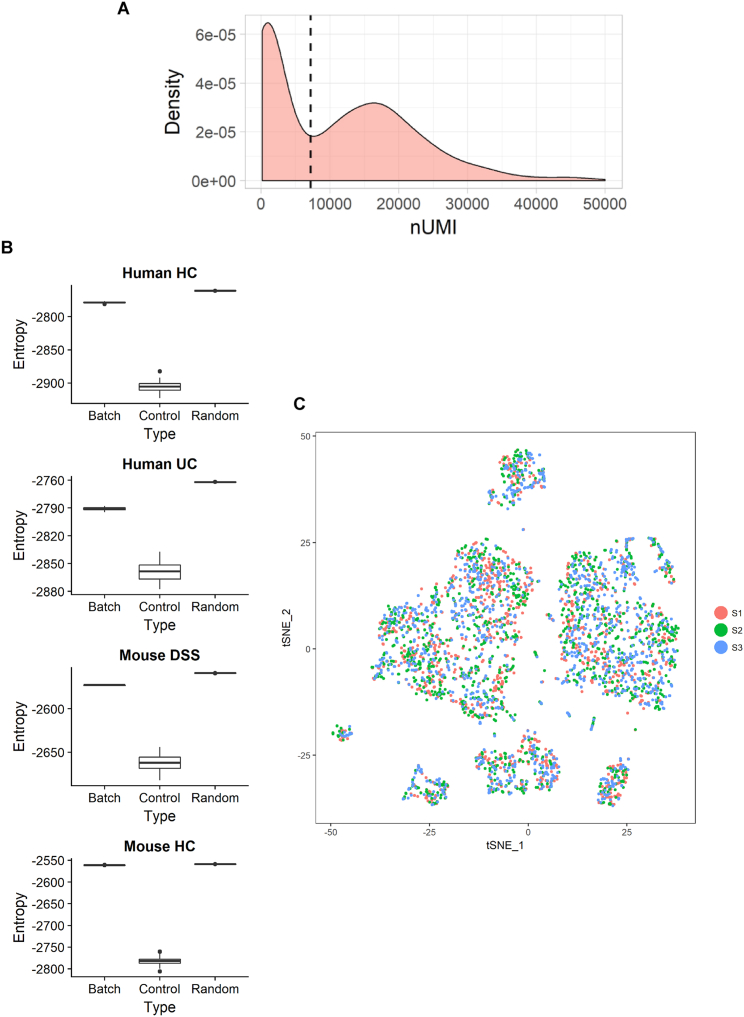
Figure S6.

Computational Analysis and Batch Effect Assessment, Related to Quantification and Statistical Analysis

(A) Identification of cellular barcodes in 10x data was selected as the first local minima across individual samples. Example distribution density and local minimum (dashed line) are shown.

(B) Batch effects in the 10x scRNA-seq data. Boxplots show the entropy of batch mixing for each dataset (Batch), compared to a negative (Random) and positive (Control) controls. For each set of data, entropy of batch mixing was computed as in Haghverdi et al., 2018. As negative controls (no batch effect), random batch labels were assigned to each cell. As a set of positive batch controls (each cluster is driven entirely by batch effect), cluster labels were used. In each dataset, the entropy of mixing for the batch effects approaches that of negative control.

(C) tSNE plot visualizing the batch distribution in healthy mouse 10x data, corresponding to S2B bottom panel.