Predicting the tissue depth for remote triggering of drug delivery systems

Abstract

Externally triggerable drug delivery systems have promising potential in providing flexible control of the timing, duration, and intensity of treatment according to patient’s needs, while reducing side effects and increasing therapeutic efficacy. However, a limitation to translating such systems into clinical practice is the difficulty to predict the tissue depth at which such systems could be safely used in vivo (e.g. activatable at the target site with a clinically-safe energy dosage). An effective method is needed to evaluate the clinical potential of externally triggerable drug delivery systems. Here we have a method and approach to predicting the tissue depth at which a drug delivery system can be safely triggered in vivo by an external energy source. We used in vitro and ex vivo experiments combined with a mathematical model to develop a method to predict activated drug release at different tissue depths, which was then validated in vivo. We constructed these models for liposomal drug delivery systems triggered by two of the most commonly studied external stimuli: ultrasound and near infrared light. We developed the approach in two prevalent tissue types: muscle and fat. Our method identified two important parameters in the activation of drug delivery systems in tissue: 1) the ability of the activation energy to penetrate tissue, 2) the sensitivity of the system to the activation source. The method was validated by correlation with triggered sciatic nerve block in the rat in vivo, demonstrating that this approach provided an accurate estimate of activated release at different tissue depths.

Introduction

Externally triggerable drug delivery systems may allow control over the timing and location of drug release or delivery events, allowing therapeutics to be released at the desired site, minimizing side effects, and enhancing efficacy of therapeutics (1, 2). More recently, externally triggerable drug delivery systems have demonstrated the ability to allow control of therapeutic intensity and duration in a repeatable and adjustable fashion by controlling the triggering parameters, such as the intensity and duration of the triggering source (3), demonstrating the potential of personalized drug delivery with these systems. Such drug delivery systems have been studied in cancer therapeutics (4, 5), pain relief (3, 6, 7), biofilm infection treatment (5), and other conditions (1, 9).

The tissue depth at which drug delivery systems can be triggered is an obviously important parameter as it determines where in the body the system can be applied. The triggering stimulus can be attenuated progressively the deeper the target. Systems that can only be triggered within a few millimeters of the body surface will only be able to reach a fraction of possible targets. This is usually the reason that near infrared (NIR) light is used in this context; it can penetrate relatively deeper into tissue when compared with UV or visible light (10, 11). The depths that can be reached will also depend greatly on the optical properties of the tissue(s) in question, penetration of light into fat being greater than that through muscle for example(12, 13). Furthermore, the depth at which the system can be triggered is an important issue in terms of safety. Greater depths can be reached by increasing the irradiance, but that can entail the risk of thermal injury. Many systems described in the literature operate at irradiances (to be more precise, energy doses = irradiance × time) that would almost certainly result in burns (9). (There are published safety standards, although they are often given in irradiances rather than energy doses (14).) These considerations have been among those that have encouraged interest in ultrasound-triggered drug delivery (15); ultrasound is generally considered to be safe at the frequencies and amplitudes used clinically, and can penetrate a wide range of tissues to a great depth (16). (However, it cannot penetrate air-filled spaces, which present little obstacle to light.)

Due to the numerous therapeutic and imaging approaches in which NIR light has been implemented, the literature presents a bewildering array of putative depths at which it has been claimed that it can be used. In consequence, it is difficult to make definitive statements about the depths at which NIR-triggered systems can be deployed, or whether they hold advantages over alternative technologies in that regard.

Here we have developed and validated an experimental method to predict the tissue depth at which drug delivery systems can be triggered. The method comprises in vitro and ex vivo experimentation, from which a mathematical model was derived. We applied the method to two NIR-triggered drug delivery systems activated by distinct mechanisms (photosensitization (3) and a photothermal effect (7)) and an ultrasound-triggered one (17). The method’s ability to predict in vivo results was tested, and the method was extended to penetration through two prevalent tissue types, muscle and fat. The key factors achieving payload release at a given tissue depth were (1) the tissue-penetrating properties of the energy source and (2) the sensitivity of the drug delivery system to the external energy.

Results

The release of payload depends on the amount of unattentuated energy that penetrates through a given depth of tissue to reach the drug delivery system and on the vehicle’s intrinsic sensitivity to the energy source. These two components were investigated in the following sections.

Energy attenuation by tissue

When energy travels through tissue, it could be absorbed or scattered, resulting in the attenuation of energy when transmitted through tissue. Energy attenuation when traveling through tissue was modeled according to the Beer Lambert’s law (11, 13).

$$I=I_0\exp \left(-\mu z\right)$$ [Eqn 1]

where I = transmitted intensity, I₀ = irradiated intensity, μ = attenuation coefficient, z = tissue thickness. Rearranging Eqn 1 gave:

$$Ln\left(\frac{I}{I_0}\right)=-\mu z$$ [Eqn 2]

The attenuation coefficient μ in Eqn 2 was obtained empirically via the following ex vivo experiments, which were performed to assess the tissue penetrating properties of energy sources. Defined thicknesses of tissues were placed between the energy source and an energy detector (optical power detector and ultrasonic receiver for light and ultrasound respectively; Fig 1a), and the transmitted intensity of 730 nm light or 1 MHz ultrasound was measured (Fig. 1, see Methods for details). With a 1 cm bovine muscle tissue barrier, 53.5 ± 13.9 % of ultrasound was transmitted (Fig. 1b), whereas only 1.9 ± 0.8 % of near infrared light penetrated. With a 2 cm muscle tissue barrier, 19.9 ± 3.4 % of ultrasound energy was transmitted and 0.15 ± 0.09 % of near infrared light. The amount of light and ultrasound energy that penetrated through tissue showed an exponential decay with respect to tissue thickness (Fig. 1).

Figure 1.

Attenuation of light and ultrasound with varied muscle tissue thicknesses. (a) Schematic of the setup for the detection of transmitted energy through tissue. Muscle tissue of varied thickness was placed between the ultrasound (1 MHz, 3 W/cm²) or light (730 nm, 250 mW/cm²) source and a detector. (b) Effect of muscle tissue thickness on transmitted intensity.

The attenuation coefficients (μ) were obtained empirically as the slope of the line relating the amount of transmitted intensity to tissue thickness (Fig. S1a). The attenuation coefficient through muscle tissue was 2.66 for light and 0.73 for ultrasound (Fig. S1a, Eqn 2), showing that ultrasound travels through tissue more efficiently than does light.

In the computations below, specific energy intensities used were normalized to the maximum safe energy dosage for the respective energy source (I_max). For 730 nm light (at a 10 min exposure), I_max was 264 mW/cm² according to the guidelines from the American National Standards Institute (ANSI) (14) (below, a maximum of 250 mW/cm² was used experimentally) and I_max for an unfocused ultrasound beam was 3 W/cm² according to guidelines from the International Radiation Protection Association (IRPA) and the World Health Organization (WHO)(18), to avoid excessive heating and tissue injury (19).

Development of a model of drug release in response to external triggers

Photosensitizer- and sonosensitizer-loaded liposomes were synthesized as previously reported (3, 17). 1,4,8,11,15,18,22,25-octabutoxyphthalocyaninato-palladium(II) (PdPC) was chosen as the photosensitizer due to its strong absorption at 730 nm(3), which lies within the near infrared window between 650 nm and 900 nm, where light can penetrate tissues more effectively(10, 20). Protoporphyrin IX (PPIX) was used as the sonosensitizer. Both agents have been shown to induce energy-triggered lipid peroxidation by producing reactive oxygen species, activating drug release upon light irradiation(3) (for photosensitizer-based systems) or insonation (for sonosensitizer-based systems) (21, 22). PdPC-loaded liposomes (Lipo-PdPC) had an average diameter of 1.27 ± 0.29 μm, and PPIX-loaded liposomes (Lipo-PPIX) had an average diameter of 1.36 ± 0.04 μm.

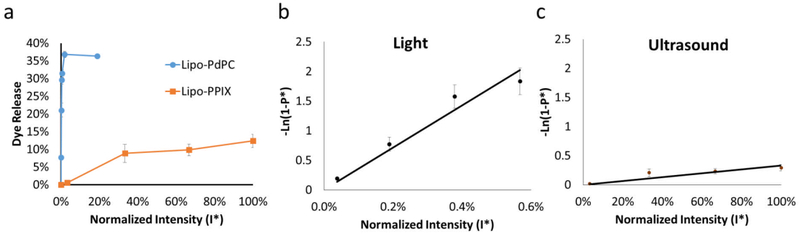
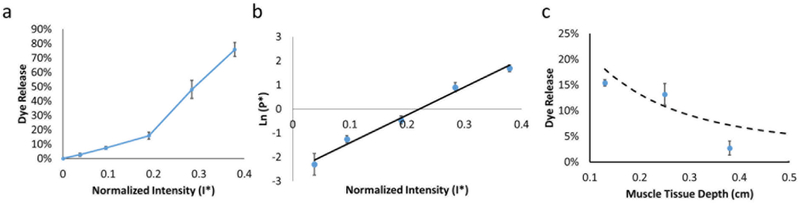
For Lipo-PdPC and Lipo-PPIX, the applied energy induces the generation of reactive oxygen species, which would then peroxidate unsaturated lipids in the lipid bilayer, increasing its permeability (denoted P) and allowing dye or drug release. To determine a metric describing the sensitivity of the drug delivery systems to their respective triggering energies, we measured the effect of normalized energy intensity I* on dye release (Fig. 2a). From those data we modeled the normalized permeability P* of the liposomes in response to the triggering energy. The relationship between I* and P* (specifically, the slope of the graph relating the log transformed permeability and normalized intensity, Figs. 2b–c) described the sensitivity S of the liposomes to energy, i.e. S reflects a system’s ability at a given energy intensity to generate reactive oxygen species from a sensitizer, peroxidize lipids, and release drug.

Figure 2.

Effect of energy intensity on sulforhodamine B release from light- (Lipo-PdPC) and ultrasound- (Lipo-PPIX) sensitive liposomes. The intensities were normalized with 100% defined as 264 mW/cm² for light and 3 W/cm² for ultrasound. (a) Effect of normalized energy intensity on dye release. (b–c) Effect of normalized energy intensity on normalized permeability (P*) of Lipo-PdPC (b) and Lipo-PPIX (c)). The curves are determined by Eqn 19. The sensitivity coefficient S is the slope of the curves. Data are means ± SD, N=4.

Having S, we developed a model to predict release at any given tissue depth when triggered by light or ultrasound. That model was then tested by assessing its ability to predict triggered effects in vivo. To validate the approach, the model was extended to a second tissue (fat), and liposomes triggered by a completely different mechanism, the plasmonic photothermal effect.

Determination of the normalized permeability (P*)

In order to establish the relationship between drug delivery vehicle permeability and our measured cargo release results, we assumed that drug diffusion from the vehicle was dependent on vehicle permeability. We modeled that relationship (drug diffusion from the vehicle with respect to liposomal membrane permeability) using the Noyes-Whitney rule:

$$V_L\frac{d{C}_L}{dt}=AP\left(C_E-C_L\right)$$ [Eqn 3]

V_L = volume of one liposome

C_L = concentration of cargo within liposome

t = time

C_E = concentration of cargo outside of liposome

A=surface area of liposome

P=permeability

Assuming that the particles were spherical and that the volume of the liposomes did not change upon triggering, which are assumptions validated in previous reports(3, 7), we could solve the differential equation in Eqn 4 to yield an equation relating the concentration of drug within the liposome to the liposome permeability and the constants mentioned above (Eqn 4):

$$\frac{C_L}{C_0}=\frac{V^{\ast }-\left(2V^{\ast }-1\right)\exp \left(-\frac{4\pi R^{2}P}{V_L}t\right)}{1-V^{\ast }\exp \left(-\frac{4\pi R^{2}P}{V_L}t\right)}$$ [Eqn 4]

V_T = total volume of the liposome solution

V^* = V_L/V_T

C₀ = initial concentration of cargo within liposome

Assuming a closed system, cargo release – determined experimentally in Fig. 2a – can be expressed as:

$$CargoRelease=1-\frac{C_L}{C_0}$$ [Eqn 5]

Inserting Eqn 4 into this term, we obtain Eqn 6 that relates cargo release to permeability:

$$CargoRelease=1-\frac{V^{\ast }-\left(2V^{\ast }-1\right)\exp \left(-\frac{4\pi R^{2}P}{V_L}t\right)}{1-V^{\ast }\exp \left(-\frac{4\pi R^{2}P}{V_L}t\right)}$$ [Eqn 6]

P cannot algebraically be isolated in Eqn 6 and so was determined computationally (see Methods) at different cargo releases. Obtained values of P were normalized (P*) with respect to P_max, the permeability at the highest dye release attained (Fig. 2a):

$$P^{\ast }=normalizedpermeability=\frac{P}{P_{\max }}$$ [Eqn 7]

Determination of the sensitivity constant S

PdPC- and PPIX-based liposomes responded to their respective energy sources by producing reactive oxygen species (ROS) that would react with unsaturated lipids (U), producing the peroxidated lipid (PL).

$$U+ROS\to PL$$ [Eqn 8]

The rate of peroxidation of the unsaturated lipid (U) to peroxidated lipid (PL) was dependent on the concentration of unsaturated lipid ([U]), reactive oxygen species ([ROS]), and a rate constant (k). Reaction kinetics were expressed as follows, consistent with previous reports(23–25):

$$\frac{d\left[U\right]}{dt}=-k\left[ROS\right]\left[U\right]$$ [Eqn 9]

where U was the unsaturated lipid, t denoted time, and k was the rate constant.

Solving the first order differential equation in Eqn 9 for [U], we derived an equation determining the unsaturated lipid concentration at any time during irradiation ([U_t]) as a function of time (Eqn 10).

$$\left[U_t\right]=\left[U_0\right]\exp \left(-k{\displaystyle {\int }_0^t\left[ROS\right]dt}\right)$$ [Eqn 10]

The generation of ROS depends on the sensitizer concentration [Sens], the normalized irradiation intensity I* (Eqn 11):

$$I^{\ast }=\frac{I}{I_{max}}$$ [Eqn 11]

and a constant K (different from the k in equation 8). From the literature (23–25) the generation of ROS from photosensitizers can be expressed as:

$$\left[ROS\right]=\left[Sens\right]\ast I^{\ast }\ast K$$ [Eqn 12]

Since energy intensity was constant over time, we substituted the three terms [Sens] * I* * K in Eqn 12 for [ROS] in Eqn 10 to derive a relationship (Eqn 13) between unsaturated lipid concentration at a given time t during ([U_t]), and normalized intensity (I*).

$$\left[U_t\right]=\left[U_0\right]\exp \left(-k{\displaystyle {\int }_0^t\left[Sens\right]\ast I^{\ast }\ast Kdt}\right)$$ [Eqn 13]

The sensitivity coefficient S, which describes ROS production (as regulated by constant k from Eqn 4) at a given energy intensity (as regulated by constant K and [Sens] from Eqn 13) can be expressed as the following (Eqn 14):

$$S=k{\displaystyle {\int }_0^{t}K\left[Sens\right]dt}$$ [Eqn 14]

Replacing the $k{\displaystyle {\int }_0^{t}K\left[Sens\right]dt}$ term in Eqn 13 by S in Eqn 14, we derive an equation (Eqn 15) that expresses that S mediates the proportion of the starting concentration of unsaturated lipid (U₀) that remains unsaturated after time t (U_t) of irradiation (I*):

$$\left[U_t\right]=\left[U_0\right]\exp \left(-I^{\ast }\ast S\right)$$ [Eqn 15]

Eqn 15 can be rearranged as a ratio of unsaturated lipid at time t (U_t), and starting unsaturated lipid (U₀), to provide an indicator of how much unsaturated lipid has been peroxidated (Eqn 16):

$$\frac{\left[U_t\right]}{\left[U_0\right]}=\exp \left(-I^{\ast }\ast S\right)$$ [Eqn 16]

The conversion of unsaturated to peroxidated lipids can be expressed as:

$$\text{Conversion}=1-\frac{\left[U_t\right]}{\left[U_0\right]}$$ [Eqn 17]

The term exp(–I* * S) in Eqn 16 can be substituted for $\frac{\left[U_t\right]}{\left[U_0\right]}$ in Eqn 17 to yield Eqn 18:

$$Conversion=1-\frac{\left[U_t\right]}{\left[U_0\right]}=1-\exp \left(-I^{\ast }\ast S\right)$$ [Eqn 18]

Here conversion is the proportion of unsaturated lipids that become peroxidated (1 = complete conversion). That conversion will drive the permeability of the liposomes. Assuming that the permeability of the drug delivery vehicle (P*) was proportional to the amount of peroxidated unsaturated lipid $\left(1-\frac{\left[U_t\right]}{\left[U_0\right]}\right),$ i.e. that Conversion = P*, P* can be related to S as in Eqn 19:

$$P^{\ast }=1-\exp \left(-I^{\ast }\ast S\right)$$ [Eqn 19]

S is solved for as the constant in Eqn 13 as described in Methods. It is worth noting that S can also be the slope of the following equation (Eqn 20):

$$-\text{ln}\left(1-P^{\ast }\right)=I^{\ast }\ast S$$ [Eqn 20]

and therefore of Figs 2 b and c.

To determine the sensitivity of the liposomes to the energy source (sensitivity coefficient S in equation 20), we first measured cargo release at given energy intensities. Liposomes were loaded with a hydrophilic fluorescent dye, sulforhodamine B (SRho), at self-quenching concentrations,i.e. so that there was only fluorescence upon release of dye. Upon SRho release from liposomes, the dye would be unquenched and fluoresce. Liposomal SRho release was measured empirically by irradiating the liposome solution with the energy source, after which fluorescence in the irradiated/insonated liposome solution was measured in a 96 well-plate (Fig. 2a). Dye release from Lipo-PdPC increased with irradiance up to an irradiance of 50 mW/cm², above which the release of dye from the photochemical effect plateaued at approximately 36% (Fig.2a). Release from Lipo-PPIX increased with insonation intensity from 0.5 ± 0.2 % at 0.1 W/cm² to 12.4 ± 1.9 % at 3 W/cm².

The dye release at each I* (Fig. 2a) was entered into Eqn 6, using the values listed in Table S1 for volume fraction of liquid (V*), calculated by subtracting the particle volume determined from TEM images from the total volume of the liposome solution; radius of particle (R), as characterized above; and duration of activation (t) to yield the normalized liposomal permeability (P*) of Lipo-PPIX and Lipo-PdPC at different activation intensities (Fig 2b). P* and its corresponding normalized energy intensity (I*) were then used in Eqn 19 to yield the sensitivity coefficient S (Eqn 14). S was 356.09 for Lipo-PdPC and 0.33 for Lipo-PPIX (Fig. 2b–c, R² = 0.94 for Lipo-PdPC, R² = 0.74 for Lipo-PPIX), indicating the drug release for a given energy dosage was much higher with Lipo-PdPC than with Lipo-PPIX, i.e. Lipo-PdPC was more sensitive to its stimulus than was Lipo-PPIX.

Activatable payload release with respect to muscle tissue depth

As noted above, S reflects a system’s ability at a given energy intensity to generate reactive oxygen species from a sensitizer, peroxidize lipids, and release drug. Here, we developed a model to determine that release at any given tissue depth.

A given normalized energy intensity I* will affect liposomes of a particular sensitivity S to result in a defined normalized permeability P* (Eqn 19). In the case where the light reaches the target liposomes through tissue of thickness z, the energy intensity emitted by the source ($I_0^{\ast }$; for 730 nm light: 250 mW/cm² for 10 min; for 1 MHz ultrasound: 3 W/cm² for 10 min) is attenuated to $I_Z^{\ast }$ (Eqn 21; cf Eqn 1)

$$I_Z^{\ast }=I_0^{\ast }\exp \left(-\mu z\right)$$ [Eqn 21]

Substituting this expression for I*into Eqn 19 to account for energy attenuation yields Eqn 22, which relates P* to the energy that reaches any given tissue depth:

$$P^{\ast }=1-\exp \left(-I_0^{\ast }\exp \left(-\mu z\right)\ast S\right)$$ [Eqn 22]

As was the case in equation 6, modeling of cargo release requires absolute permeability P – in this case at a given tissue depth, P_z – rather than normalized permeability P*. Given Eqn 7, that was achieved by multiplying both sides of Eqn 22 by P_max, yielding Eqn 23:

$$P_Z=P_{max}\ast \left(1-\exp \left(-I_0^{\ast }\exp \left(-\mu z\right)\ast S\right)\right)$$ [Eqn 23]

This expression for P was substituted into Eqn 6 to yield Eqn 24, the effect of the attenuated irradiation intensity after traveling through the tissue on the sensitivity of the drug release vehicle and cargo release:

$$CargoRelease=1-\frac{V^{\ast }-\left(2V^{\ast }-1\right)\exp \left(\frac{4\pi R^2{P}_{max}\left(1-\exp \left(-I_0^{\ast }\exp \left(-\mu z\right)\ast S\right)\right)}{V_L}t\right)}{1-V^{\ast }\exp \left(-\frac{4\pi R^2{P}_{max}\left(1-\exp \left(-I_0^{\ast }\exp \left(-\mu z\right)\ast S\right)\right)}{V_L}t\right)}$$ [Eqn 24]

where $I_0^{\ast }$ is the normalized irradiated intensity unattenuated by travel through tissue. Equivalently, Eqn 24 can also be written explicity in terms of the permeability at a given tissue depth z:

$$CargoRelease=\text{1}-\frac{V^{\ast }-\left(2V^{\ast }-1\right)\exp \left(\frac{4\pi R^2{P}_Z}{V_L}t\right)}{1-V^{\ast }\exp \left(-\frac{4\pi R^2{P}_Z}{V_L}t\right)}$$ [Eqn 25]

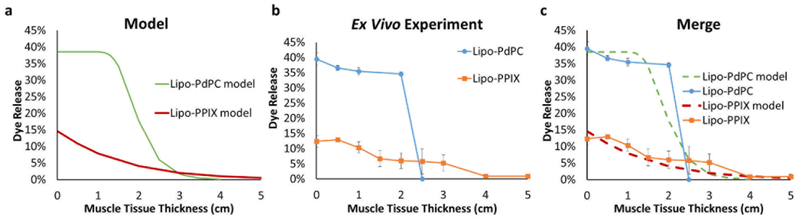
The release profiles from Lipo-PdPC and Lipo-PPIX at different tissue depths could be modeled with Eqn 24 using the attenuation (p) and sensitivity coefficients (S) obtained from Figs. 1 and 2, across a range of values of T from 0 to 5 cm. The computational model (Fig 3a, 3c). showed that triggering of Lipo-PdPC would cause more dye release at muscle tissue depths < 3 cm than would triggering of Lipo-PPIX (Fig. 3), due to the higher sensitivity of Lipo-PdPC to the triggering energy (Fig. 2).

Figure 3.

Modeling and empirical ex vivo results of payload release triggered from Lipo-PdPC and Lipo-PPIX at varied muscle tissue depth. (a) The model was computed from Eqn 19 with the attenuation coefficient (p.) and the sensitivity coefficient (S) derived from Figs. 1 and 2 respectively (see text). (b) Ex vivo payload release measured at different tissue depths; data are mean ± std, N=4). (c) Comparison of modeling and empirical results.

To mimic triggering at various tissue depths, defined thicknesses of bovine muscle tissue were placed between the energy source and dye-loaded liposomes in PBS solution. The release of dye at various tissue depths was measured by quantifying the fluorescence of the liposomal solution (Fig. 3b), which indicated the amount of released and therefore unquenched SRho. In the absence of interposed tissue, Lipo-PdPC released 39.5 ± 2.0 % of payload under irradiation with 730 nm light (250 mW/cm² for 10 min). At the same irradiation conditions the payload release decreased slightly to 34.6 ± 0.7 % as the thickness of the muscle barrier increased to 2 cm. However, triggered payload release dropped to zero as the muscle tissue barrier increased to 2.5 cm. In the absence of a tissue barrier, Lipo-PPIX released 12.4 ± 1.9 % upon insonation (1 MHz, 3 W/cm², 10 min). Payload release decreased steadily with increasing tissue barrier thickness, reaching 5.2 ± 2.6 % at 3 cm and 0.9 ± 0.3 % at 4 cm.

Our ex vivo results correlated very well with the modeling results (Fig. 3c; R² = 0.91 for Lipo-PPIX and 0.72 for Lipo-PdPC, Fig. S3), where Lipo-PdPC released more drug than Lipo-PPIX at lesser tissue depths but comparable amounts of drug at greater tissue depths.

Effect of tissue depth on stimulus-triggered nerve block in vivo

To validate in vivo the mathematical model developed from ex vivo data, we investigated its correlation with the performance of externally-triggered local anesthetic liposomes at varying tissue depths in vivo.

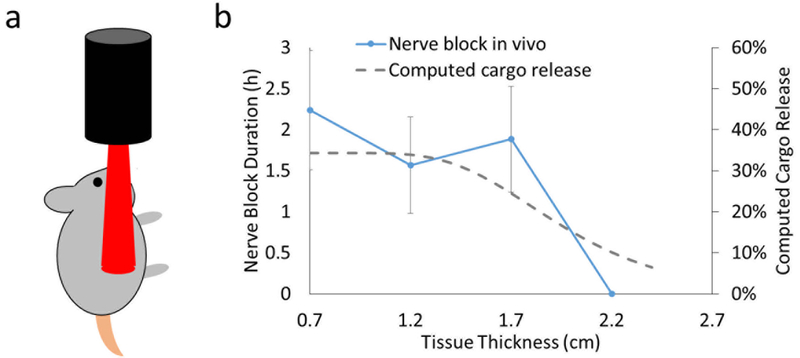
Modeling with Eqn.24 (dashed line in Fig. 4) predicted that payload release would be relatively constant between 0.7 and 1.2 cm, with an estimated release of 36%, but would decrease after approximately 1.5 cm. At 2.2 cm the estimated release was 8%.

Figure 4.

Comparison of modeled drug release and experimental determination of in vivo nerve block duration at varied muscle tissue thicknesses. Rats were injected at the sciatic nerve with Lipo-PdPC-TTX and nerve block was monitored with a modified hot plate test (see Methods). Irradiation with a 730 nm light (250 mW/cm², 10 min) was performed after the initial nerve block was resolved. Tissue thickness was varied by interposing muscle tissue of varied thickness between the rat and the light source. (a) Schematic of irradiation in vivo. (b) Nerve block duration with respect to tissue thickness and comparison with computed cargo release. As the sciatic nerve is located 0.7 cm below the skin, 0.7 cm was the baseline tissue thickness. The modeling from Eqn 19 (see Methods) is on the right axis, experimental data on the left. Data are mean ± std, N=4.

Lipo-PdPC was loaded with the local anesthetic tetrodotoxin (TTX) (3, 6). Animals were then injected with Lipo-PdPC at the rat sciatic nerve, followed by neurobehavioral testing with a modified hot plate test (see Methods) to quantify nerve block. TTX-loaded Lipo-PdPC produced a nerve block lasting 12.1 ± 5.0 h. After the initial nerve block resolved (see Fig. S4), a return of nerve block was triggered by irradiating the site of injection at 730 nm for 10 min, 250 mW/cm², inducing release of TTX(3). The rat sciatic nerve is 0.7 cm beneath the surface of the skin. In different groups of animals, the distance the light had to travel through tissue to reach the nerve was increased by interposing 0.5 cm increments of ex vivo muscle on the skin surface (Fig. 4).

In vivo results followed the same pattern as the computed model. At a tissue depth of 0.7 cm (i.e. no additional interposing muscle), the duration of triggered nerve block was approximately 2 h. The duration of triggered block remained approximately constant up to a depth of approximately 1.7 cm. When the tissue thickness increased to 2.2 cm, no nerve block was observed.

The in vivo data therefore validated the model based on parameters determined in ex vivo experiments (Fig. S5), i.e. nerve block in vivo correlated very well with drug release ex vivo (R² = 0.79).

Payload release in fat tissue

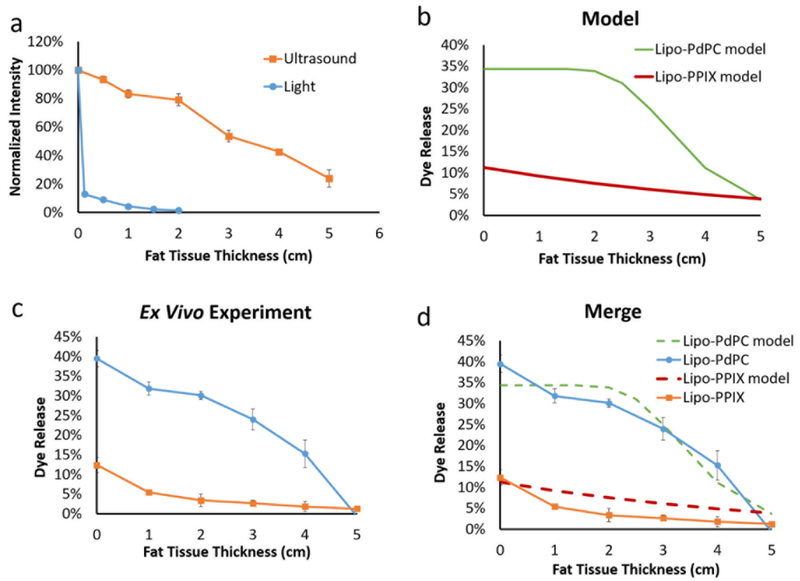
External energy travels through a wide range of tissue types, such as muscle and fat. To demonstrate applicability of the theoretical model to triggered release in other types of tissue, we performed experiments analogous to those shown above using fat tissue as the penetration barrier between the energy source and the energy detector (Fig. 5a). Only 1.3% of light energy penetrated through 2 cm of fat (8.67 times more than through muscle, p = 0.0001, Fig. S6), whereas 79.2% of ultrasound energy penetrated through the same thickness (4 times more than through muscle, p < 0.0001, Fig. S6). The attenuation coefficient (μ, Fig. S1) of light traveling through fat was 1.26, and of ultrasound was 0.91. Using the attenuation coefficients for fat and the sensitivity coefficient (Fig.2) in Eqn 24 to model drug release predicted that light-triggered Lipo-PdPC would release more dye than ultrasound-triggered Lipo-PPIX at fat tissue depths up to 5 cm (Fig.5b). Subsequent experimental results (Fig.5c; the experiment was analogous to that in Fig, 3b but using fat) confirmed that the model predicted ex vivo findings (Fig.5d).

Figure 5.

Modeling and empirical ex vivo results of energy attenuation and payload release triggered from Lipo-PdPC and Lipo-PPIX at varied fat tissue depth (a) Effect of fat tissue thickness on transmitted intensity (b) The model was computed from Eqn 19 with the attenuation coefficient derived from panel (a) (Fig. S1b) and the sensitivity coefficient from Fig. 2. (c) Ex vivo payload release at varied fat tissue depths. (d) Comparison of the modeling and experimental results.

Since tissue attenuation was the main limiting factor for light-triggered Lipo-PdPC, the decrease in attenuation in fat greatly increased the depth at which Lipo-PdPC could be effectively triggered, from 2 cm in muscle to 4 cm in fat. Figure S7 shows that Lipo-PdPC releases 23 times more payload with a 3cm fat tissue penetration barrier when compared with using muscle tissue of the same thickness. For Lipo-PPIX, where the main limitation to cargo release was liposomal sensitivity, the decrease in attenuation did not enhance the tissue depth at which it could be effectively triggered; at 4 cm depth the cargo release for both tissues was below 2 %.

Photothermal activation of gold nanorod-loaded liposomes

Externally-triggerable drug delivery systems can be activated through a wide range of mechanisms(7). To show that the derived model could be applicable to other triggering mechanisms, we synthesized gold nanorod (GNR)-loaded liposomes (Lipo-GNR) as previously reported(7). Unlike sensitizer-loaded liposomes, GNR-loaded liposomes interact with light through photothermal effects mediated by surface plasmon resonance(7). The photothermal heating induces phase transformation of the lipid bilayer to enhance the membrane’s fluidity and permeability, and hence drug release. Light-induced heating from gold nanorods has been described (27, 28) by:

$$\Delta T=\frac{\sigma \ast I}{4\pi K_{m}r}=T\ast I$$ [Eqn 26]

where ΔT is the temperature difference between steady-state temperature and initial temperature, σ = absorption cross section, I = irradiation intensity, K_m = thermal conductivity of the surrounding medium, r = distance from the center of the nanoparticle. T is the temperature increase for a given irradiation intensity over a defined time interval.

The permeability of liposomes with respect to temperature has been studied both theoretically (29) and empirically (30), and it has been found that the permeability scales exponentially with temperature and can be expressed as :

$$P^{\ast }=\exp \left(A\Delta T+b\right)$$ [Eqn 27]

where A reflects how permeability scales with temperature, and b is a constant that reflects the basal permeability at the initial temperature.

To describe the dependence of drug vehicle permeability on irradiation intensity, the term ΔT in Eqn 27 was replaced by T * I (right side of Eqn 26), yielding:

$$P^{\ast }=\exp \left(\text{A}\ast \text{T}\ast \text{I}+b\right)$$ [Eqn 28]

The sensitivity of liposome to photothermal effects S_PT can be expressed as the product of the temperature change and the coefficient A from Eqn 27

$$S_{PT}=\text{A}\ast \text{T}$$ [Eqn 29]

Substituting S_PT for A * T in Eqn 28 to yield Eqn 30:

$$P^{\ast }=\exp \left(S_{PT}\ast I^{\ast }+b\right)$$ [Eqn 30]

S_PT and b were determined computationally as described in Methods. (We also note that S_PT the slope of the following equation, Fig. 6b)

$$S_{PT}\ast I^{\ast }=\text{ln}\left(P^{\ast }\right)$$ [Eqn 31]

Figure 6.

Modeling and experimental results of dye release from gold nanorod-loaded liposome (Lipo-GNR) at varied muscle tissue depths. (a) Effect of light intensity on Lipo-GNR payload release and (b) Effect of normalized energy intensity on normalized permeability. The sensitivity coefficient S_PT is the slope of the curve. (c) The model of dye release at varied tissue depths (dashed curve) was compared with ex vivo experimental results (blue data points). Data are mean ± std, N=4.

Permeability of Lipo-GNR-based was calculated by substituting the definition of transmitted irradiance intensity (I_z; Eqn 21), into Eqn 30 yielding:

$$P^{\ast }=\exp \left(S_{PT}\ast I_0^{\ast }\exp \left(-\mu z\right)+b\right)$$ [Eqn 32]

The absolute permeability P_z of the liposome system at a given tissue depth can then be written as:

$$P_Z=P_{max}\exp \left(S_{PT}{I}_0^{\ast }\exp \left(-\mu z\right)+b\right)$$ [Eqn 33]

The value from P can then be substituted for P in Eqn 6 to model cargo release for a given unattenuted irradiance and tissue depth for Lipo-GNR:

$$CargoRelease=1-\frac{V^{\ast }-\left(2V^{\ast }-1\right)\exp \left(-\frac{4\pi R^2{P}_{max}\exp \left(S_{PT}{I}_0^{\ast }\exp \left(-\mu z\right)+b\right)}{V_L}t\right)}{1-V^{\ast }\exp \left(-\frac{4\pi R^2{P}_{max}\exp \left(S_{PT}{I}_0^{\ast }\exp \left(-\mu z\right)+b\right)}{V_L}t\right)}$$ [Eqn 34]

The attenuation coefficient μ for the trigger, 730 nm light, was determined from Fig.1. To determine S_PT for Lipo-GNR, SRho was loaded into Lipo-GNR and dye release at different irradiation intensities was measured (Fig. 6a). Absolute irradiation intensities used ranged from 0 mW/cm² to 100 mW/cm², the highest intensity at which the light induced heating did not cause the liposome solution to dry up. The amount of released dye and its corresponding energy intensity were entered into Eqn 26, to provide P* at each activation intensity. P*and its corresponding activation intensity were entered into Eqn 30, from which S_PT and b were determined (Fig. 6b; S_PT = 11.6; b = −2.56). Those constants were used in Eqn 34, to create a model predicting the release of dye from Lipo-GNR at a given tissue depth (Fig. 6c, dashed line).

To validate this model empirically, dye release was quantified by measuring the fluorescence of the liposome solution at various tissue (muscle) depths upon irradiation (730 nm, 250 mW/cm², 10 min) or insonation (1 MHz, 3 W/cm², 10 min) (individual points in Fig. 6c). The model correlated well with the ex vivo experimental results. The model and empirical data were further validated in vivo by our observation that TTX-loaded Lipo-GNR did not trigger sciatic nerve block upon irradiation at 250 mW/cm² (Fig. S8): the rat sciatic nerve is embedded under approximately 0.7 cm of tissue, at which Fig. 6c would predict that negligible payload release would occur.

Discussion

We have described a method that incorporates data from in vitro and ex vivo experiments to model the relationship between energy attenuation, vehicle sensitivity, and dye release, and allows the prediction of triggerable drug release from a particular delivery system at a given tissue depth stimulated by an external energy source. This method provides an empirical framework for assessing the clinically important matter of the tissue depth at which a triggerable drug delivery system will safe and be effective.

The ability of an energy stimulus to penetrate tissue is a key parameter if triggering of drug delivery systems in deep tissues is intended. In this study, ultrasound had an attenuation coefficient 3.64 times lower than near infrared light in muscle (Fig. 1). (Moreover, although near infrared light penetrates tissues more effectively than UV and visible light, it is still markedly attenuated by tissue; Fig.1.) Nonetheless, at muscle tissue depths from 0 to 2 cm, drug release from Lipo-PdPC under 5 mW/cm² NIR irradiation was greater than from Lipo-PPIX at 3W/cm² insonation (Fig. 2). This observation demonstrates the importance of a drug delivery system’s sensitivity to the triggering energy in determining its release profile, and thus therapeutic efficacy, at different tissue depths.

The parameters in the model could be obtained by two relatively simple in vitro / ex vivo experiments: 1) the tissue attenuation profile of the energy source, which gives information on the interaction between the energy source and the penetrated tissue (Fig. 1); 2) the release of dye at different energy intensities, which provides the sensitivity of the vehicle to the energy source (Fig. 2). Obtaining such information in vitro/ ex vivo may be more cost-effective and time-efficient than in vivo experiments. Indeed, our in vivo results correlated strongly with the modeling results (Fig. 4), suggesting that the model provided a reasonable estimation of the tissue thickness at which a given delivery system could be triggered. Furthermore, the model could be used with different triggering mechanisms, including the photochemical mechanism of Lipo-PdPC and the photothermal mechanism of Lipo-GNR (Fig. 6).

The payload release profile with liposomes encapsulating the fluorescent dye sulforhodamine reasonably correlated with the in vivo nerve block experiments (Fig.4), where the drug delivery vehicle was loaded with the local anesthetic tetrodotoxin. Given that the model works for both hydrophilic compounds, we expect that this equation could be extended to other hydrophilic drug molecules. It remains to be determined whether this approach should be modified with drugs of other chemical properties.

The model in this study provides a framework for an effective estimation of the clinical potential of externally triggerable drug delivery systems, applicable to different triggeringsources such as light and ultrasound. Further improvements of the model may take into account the complexity of in vivo systems. The in vivo model was not dependent on a mere triggered release event, but on the effect of tissue depth on energy penetration, the heterogeneous nature of the tissues (unlike the homogeneous tissues used here), the effect of irradiance on drug release, drug penetration into nerve, interruption of nerve function in a living animal, diffusion of drug back out of nerve leading to resolution of nerve block. Even in a much simpler model, nerve block from injected free local anesthetics, there is considerable variability. As a result, the model could be further fine-tuned by, for example, incorporating the effects of temperature on diffusion, the effects of basal drug release (vs. only triggered release due to lipid peroxidation), etc.

In the current model, the concentration of the drug delivery vehicle was known in vitro, ex vivo, and in vivo (at least at the time of injection) in a local depot system. This allowed accurate modeling, as demonstrated by the correlation with in vivo results (Fig. 4). The modeling would likely be more complicated for a drug delivery system that was delivered systemically but accumulated locally, as the concentration of the drug delivery system at the target site would change over time(31) in a manner dependent on the microenvironment of the target site, such as the leakiness of the vessel or tumor volume (32). In that case, the model as is could still be useful for determining the extent to which triggering could occur at a given tissue depth, but it might need to be modified by additional pharmacokinetic and/or biodistribution parameters to be able to predict the response to triggering over time.

In conclusion, an approach for the prediction of the tissue depth at which externally triggerable drug delivery systems could be activated was developed and a cost-effective, time-efficient method to evaluate the clinical relevance of such systems was presented. The tissue penetrating properties of the energy source and the sensitivity of the system to the trigger were found to be the key parameters when evaluating the clinical potential of such systems. This work provides a method with which externally triggerable drug delivery systems could be practically designed for its clinical potential and target tissue.

Materials and Methods

Liposome synthesis.

Photosensitizer 1,4,8,11,15,18,22,25-octabutoxyphthalocyaninato-palladium(II) (PdPC) was synthesized using the metal-insertion method as previously reported(3, 33). Gold nanorods (GNR) were synthesized by a seed-mediated growth method based on previous reports(34). Sonosensitizer protoporphyrin IX (PPIX) was purchased from Sigma-Aldrich (St. Louis, MO, USA). Liposomes were prepared via the thin-film hydration method (3). PdPC- and PPIX-based liposomes were formed by the following lipid formulation: 1,2-distearoyl-sn-glycero-3-phosphocholine (DSPC, Avanti Polar Lipids, Alabaster, AL, USA), 1,2-dilinoleoyl-sn-glycero-3-phosphocholine (DLPC, Avanti Polar Lipids, Alabaster, AL, USA), 1,2-distearoyl-sn-glycero-3-phosphatidylglycerol (DSPG, Genzyme, Cambridge, MA, USA), and cholesterol (Sigma, St. Louis, MO, USA) at molar ratio 3:3:2:3] and PdPC or PPIX (0.2% molar ratio of total lipid content). GNR-based liposomes were prepared with the following lipid formulation: 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC, Avanti Polar Lipids, Alabaster, AL, USA), 1,2-dipalmitoyl-sn-glycero-3-phospho-(1’-rac-glycerol) (DPPG, , Avanti Polar Lipids, Alabaster, AL, USA), cholesterol and Poly(ethylene glycol) 2-mercaptoethyl ether thiol (HS-PEG-DSPE, Nanocs, New York, NY, USA) (molar ratio 6:2:30.2). The lipid formulations were dissolved in a chloroform : methanol (v/v, 9:1) solution. The solution was removed by a rotary evaporator (Buchi, New Castle, DE). Tert-butanol was added to the lipid thin film and was lyophilized overnight to form a lipid cake. The lipid cake was then hydrated with PBS, 10 mg/mL sulforhodamine B (SRho, Sigma, St. Louis, MO, USA), 0.375 mg/mL tetrodotoxin (Abcam, Cambridge, MA, USA) and/or GNR solution (0.5 mg/mL). The liposome solution was dialyzed for 48 h prior to use.

Liposome characterization.

Liposome size was determined by dynamic light scattering (Delsa Nano C, Beckman Coulter, Brea, CA). SRho loading was determined by UV-Spectroscopy (λmax = 560 nm). Tetrodotoxin loading was assessed by ELIZA (Reagen, Moorestown, NJ).

Quantification of energy attenuation and cargo release measurement with ex vivo tissue.

Bovine muscle (eye round steak) and fat tissue (pig fat) were purchased from local butcher shops. Tissue thickness was quantified by a caliper. The tissues were cut to the indicated thicknesses. The intensity of light after penetration through tissue was quantified by an optical power meter (Thor labs, Newton, NJ, USA), during which tissue was placed between the light beam and the optical power meter. Ultrasound intensity was quantified by an ultrasonic receiver (Olympus, Tokyo, Japan) and ultrasound penetration through tissue was determined by placing the tissue between the ultrasound transmitter and the receiver. Unless otherwise stated, the applied ultrasound had the following parameters: 1 MHz, 3 W/cm², 10 min, continuous; and the applied light had the following parameters: 730 nm, 250 mW/cm², 10 min.

To measure the ex vivo liposomal cargo release, liposome solutions were exposed to ultrasound (1 MHz) or light (730 nm) with or without tissue in between at the indicated intensity for 10 min. SRho release from liposomes was quantified the fluorescence of the solution (Excitation/Emission = 530 nm /560nm) as previously reported (7, 35).

Numerical Iteration.

The numerical solutions of parameters were obtained using the fixed point iteration Newton-Raphson method with Goal Seek in Microsoft Excel (Microsoft Corporation, WA) as previously reported (36–39). The numerical solutions were then used as described in Results.

Animal Studies.

Animal studies followed the guidelines of the International Association for the Study of Pain and were conducted complying with protocols approved by the Boston Children’s Hospital Animal Care and Use Committee. Adult male Sprague-Dawley rats (Charles River Laboratories, Wilmington, MA, USA) of 350–450 g were housed under a 12-h/12-h light/dark cycle with lights on at 7:00 AM. After anesthetized by isoflurane-oxygen, rats were injected with 200 μL ofTTX-loaded Lipo-PdPC at the sciatic nerve using a 23 G needle. A detailed description of rat sciatic nerve injections could be referenced elsewhere (40). Irradiation with 730 nm light (10 min, 250 mW/cm²) or insonation with 1 MHz (10 min, 3 W/cm²) ultrasound was performed after the initial nerve block was resolved. Bovine muscle tissue with the indicated thickness was placed between the triggering source and the rat.

Nerve block was quantified by a modified hotplate test (41), where the rat’s hindpaw was placed on a hotplate of 56 °C. The duration between the placement and withdrawal of the rat’s hindpaw was recorded and termed as “thermal latency”. A normal rat without any nerve block would have a baseline thermal latency of 2s, whereas the maximum thermal latency was capped at 12 s, after which the rat’s hindpaw was manually removed from the hotplate, to prevent thermal injury. Nerve block was defined as a thermal latency > 7s.