Abstract
In most technological applications, nanoparticles are immersed in a liquid environment. Understanding nanoparticles/liquid interfacial effects is extremely relevant. This work provides a clear and detailed picture of the type of chemistry and physics taking place at the prototypical TiO2 nanoparticles/water interface, which is crucial in photocatalysis and photoelectrochemistry. We present a multistep and multiscale investigation based on hybrid density functional theory (DFT), density functional tight-binding, and quantum mechanics/molecular mechanics calculations. We consider increasing water partial pressure conditions from ultra-high vacuum up to the bulk water environment. We first investigate single water molecule adsorption modes on various types of undercoordinated sites present on a realistic curved nanoparticle (2–3 nm) and then, by decorating all the adsorption sites, we study a full water monolayer to identify the degree of water dissociation, the Brønsted–Lowry basicity/acidity of the nanoparticle in water, the interface effect on crystallinity, surface energy, and electronic properties, such as the band gap and work function. Furthermore, we increase the water coverage by adding water multilayers up to a thickness of 1 nm and perform molecular dynamics simulations, which evidence layer structuring and molecular orientation around the curved nanoparticle. Finally, we clarify whether these effects arise as a consequence of the tension at the water drop surface around the nanosphere by simulating a bulk water up to a distance of 3 nm from the oxide surface. We prove that the nanoparticle/water interfacial effects go rather long range since the dipole orientation of water molecules is observed up to a distance of 5 Å, whereas water structuring extends at least up to a distance of 8 Å from the surface.
Keywords: titanium dioxide, nanospheres, curved surface, surface acidity/basicity, solid/liquid interface, DFT, QM/MM, molecular dynamics
1. Introduction
The short- and long-range interactions between water and titanium dioxide surfaces are of paramount relevance in many technological applications, ranging from the traditional use of TiO2 in the pigment industry or in advanced fields, such as photocatalysis, photoelectrochemistry, fuel production, and nanomedicine. This is because in these very diverse applications TiO2 materials are employed in an aqueous or wet environment. Water should not be considered as a mere spectator of the physical and chemical processes at the metal oxide surface but, on the contrary, it is probably often an active actor in many respects.1,2 First, it competes with any other chemical species for adsorption on surface sites as a donor on low-coordinated Ti atoms and as an H-bonding species on low-coordinated O atoms. Secondly, water dissociation at surface sites or defects leads to the formation of OH species, which are crucial functional groups for the surface chemistry, functionalization, and molecular anchoring. Additionally, water mono or multilayer adsorption may alter the surface electronic properties and work function, as well as the surface energy leading to different reconstructions than in ultra-high vacuum conditions.3 Recently, it was even reported to affect the trapping dynamics of photogenerated charge carriers in TiO2.4,5
Given the recognized importance of water on TiO2, several first-principles studies have investigated the detailed atomistic description of water chemistry and multilayer dynamical structures on low-index flat surfaces.6−9 However, in practical applications, TiO2 is mostly used in the form of nanoparticles, which, in a diluted aqueous environment, may partially dissolve and become round shaped. The curvature present in spherical nanoparticles or in nanorods leads to the exposition of a larger number of undercoordinated sites and to a further surface tension that are expected to largely affect their interaction with a water environment.
Modeling of the curved systems is in more demand than the flat ones because a realistic size of the nanosystem must be considered to not exaggerate the curvature effect and not to induce excessive strain. Nanoparticle models with a definite crystalline phase should contain at least 500–1000 atoms with a diameter size of at least 2 nm, which is the lower limit of the experimentally prepared TiO2 nanoparticles.10−15 Few water multilayers around this nanoobject easily sum up to 2000–2500 atoms. On top of this, a bulk of water surrounding the hydrated nanoparticles clearly leads to an extremely large model.
Therefore, on one hand, there is a need for models of several thousands of atoms. On the other hand, there is a requirement of reliable accuracy in the description of the complex physics and chemistry of water,16,17 especially when in contact with spherical-shaped TiO2 nanoparticles. For this, one must resort to first-principles approaches18,19 that properly describe bond breaking at the interface, fine structural details, and electronic effects given the limits of classical force-field methods in these respects.20−22 A bond order-based force field could be an alternative choice. Unfortunately, in this specific case of anatase TiO2/water interface, reaxFF is found to favor water dissociation with respect to molecular adsorption, in net contrast with various density functional theory (DFT) studies23−27 and, most importantly, in contrast with the experimental data from temperature programmed desorption measurements28 and scanning tunneling microscope imaging.29
In this work, we push the boundaries of the state-of-the-art and present a set of hybrid density functional calculations (B3LYP)30,31 on a spherical anatase TiO2 nanoparticles with a diameter of 2.2 nm with an increasing water coverage from a single molecule up to a full monolayer (ML). At this very high level of theory, first, we can correctly describe the electronic structure of the system, the band gap, and the band edges with respect to the vacuum; secondly, we can accurately describe the site and coverage dependency of the water adsorption mechanism (molecular and/or dissociative modes). Many key questions are still open on the chemistry of water molecules on a curved surface presenting several undercoordinated surface sites, whose basicity/acidity may be quite different from those on the flat surface.
As a further step, we then resort to a fast, efficient but still accurate method, the self-consistent charge density functional tight-binding (SCC-DFTB),32 to increase the number of water layers around the nanosphere (NS), up to a thickness of about 1 nm. This allows expanding the investigation into the dynamical regime through several molecular dynamics simulations to not only learn about water structuring around the nanoparticle but also about the nanoparticle structuring upon the water multilayer effect. On top of this, we have simulated a whole bulk of water around the fully hydrated nanoparticle (up to 3 nm from the surface) by using a combined quantum mechanics/molecular mechanics (QM/MM) approach (i.e., SCC-DFTB/MM), where the force-field description is only applied to the water above 1 nm from the surface.
The theoretical simulations are analyzed in comparison with the documented experimental data on controlled surface hydration of anatase TiO2 spherical nanoparticles (in the range between 2.4 and 7.7 nm) from soft and standard X-ray spectroscopy,33−351H NMR spectroscopy,36 thermogravimetric analysis,34,37 infrared spectroscopy,4,5,34 electron paramagnetic resonance spectroscopy,34 vis-infrared sum frequency generation (SFG),38,39 Brunauer–Emmett–Teller surface area analysis,37 transmission electron microscopy,4,5,33,34 analytical measurements,40−42 etc. These studies provide a direct observation of the presence of OH groups on the surface, an estimation of their density, surface heterogeneity, water layering, and surface reconstruction. When this information is combined to reliable first-principles model calculations, we achieve a deep understanding of water chemistry at the nanoparticle surface.
Our multistep and multiscale investigation provides, for the first time, an accurate description at the electronic and atomistic level of a realistic TiO2 spherical nanoparticle (700 atoms) surrounded by explicit water multilayers and bathed into a bulk of water (8958 H2O molecules). We present a specific example of interface (TiO2 nanosphere/water) because it is of high relevance in many semiconducting oxide technological applications; in a broader context, our study is also a prototype example for other complex nanostructured inorganic material/water interfaces. Understanding the fundamental properties of such interfaces is crucial for the development of nanoparticle-based applications.
2. Computational Methods
In this theoretical investigation, we mostly used two levels of theory: DFT(B3LYP) and SCC-DFTB. Both methods have been employed for electronic structure calculations and geometry optimization, whereas the molecular dynamics simulations have been performed only by using the computationally efficient self-consistent charge density functional tight-binding (SCC-DFTB) approach.
2.1. Electronic Structure Calculations
All the DFT geometry optimizations and electronic structure calculations have been carried out with the CRYSTAL14 code,43 where the Kohn–Sham orbitals are expanded in Gaussian-type orbitals (all-electron basis sets are O 8-411(d1), Ti 86-411(d41), and H 511(p1)). All forces were relaxed to less than 4.5 × 10–4 au. The B3LYP hybrid functional30,31 has been employed in this study to correctly describe the electronic structure of the anatase TiO2.
For all the SCC-DFTB calculations, the DFTB+ open source code has been used.44 The SCC-DFTB approach is an approximated DFT-based methodology derived from the second-order expansion of the Kohn–Sham DFT total energy with respect to the fluctuations of the electron density. Assuming this decomposition, the SCC-DFTB total energy can be written as
| 1 |
where, the first term in the equation represents the attractive tight-binding energy, in which the one-electron eigenvalue εi is derived from the diagonalization of an approximated Hamiltonian matrix, Erep,αβ(Rαβ) is a pairwise repulsive potential dependent on the distance between the pair of atoms α and β, which is an approximation of the short-range repulsion term, Δqα and Δqβ are the charges induced on the atoms α and β, respectively, and γαβ is a Coulombic-like interaction potential. This method has been employed with success to calculate, with an extremely reduced computational effort in comparison with standard DFT, the properties of the extended systems such as bulk TiO2 and TiO2 surfaces as well as TiO2 clusters of different sizes, giving results in good agreement with the ab initio (DFT) refs (45−47). Further details about the DFTB method and its derivation can be found in refs (32, 48), and (49). In the following, DFTB will be used as a short form for SCC-DFTB.
In this work, we employed the recently developed MATORG + HBD set of parameters,50 which has been demonstrated to be well-suited for the description of the water/water/anatase interface. This parametrization set derives from the combination of the available “matsci-0-3”51 and “tiorg-0-1”47 sets for the description of TiO2 systems. Furthermore, to improve the accuracy in the description of H-bonds, the γαH potential has been modified with a hydrogen-bonding damping function,52 with an exponent equal to 4.0. For geometry relaxations, the threshold for the convergence of the self-consistent charge (SCC) procedure was set to 10–6 charge au and forces were relaxed to less than 10–4 au.
2.2. Models of the Nanoparticles
The anatase TiO2 nanosphere (NS) model used throughout this work has been designed through global optimization with a simulated annealing process at the DFTB level of theory in a previous work by some of us.53 In this work, full geometry optimization was performed also at the DFT(B3LYP) level of theory. Here, we have further reoptimized the DFTB geometry with “MATORG + HBD” parametrization, whereas we will make use of the DFT(B3LYP) structure from ref (53). The stoichiometry of the model is (TiO2)223·10H2O and it is characterized by an equivalent diameter of 2.2 nm. The faceted anatase TiO2 nanoparticle model (NC) has a stoichiometry of (TiO2)260·10H2O and the procedure used to build this model is detailed in ref (54).
Starting geometries for the optimization of the adsorbed water monolayer have been constructed by saturating molecule by molecule the undercoordinated titanium atoms on the surface of the NS model. The initial geometry for the water multilayer on the NS model has been generated using the PACKMOL code.55 Using this program, a spherical water shell with an internal radius of 15 Å and an external radius of 21 Å has been generated around the NS with an optimized water monolayer already adsorbed. The water shell has been filled with 824 nonoverlapping water molecules, corresponding approximately to three water layers with a density of 0.0334 molecules/Å3 (1 g/dm3).
2.3. Molecular Dynamics Setup and Structural Analysis Tools
Born–Oppenheimer molecular dynamics (BO-MD) within DFTB of the water multilayers on the NS model has been carried out within the canonical ensemble (NVT). The Newton’s equations of motion were integrated with the Velocity Verlet algorithm and a small time step of 0.5 fs ensured reversibility. During the MD simulation, a constant temperature of 300 K has been maintained by using the Nosé–Hoover thermostat. The system has been equilibrated for 5 ps and, then, a production run has been performed for 45 ps. No water molecules have been observed to desorb from the system into the vacuum.
The direct-space extended X-ray adsorption fine structure (EXAFS) spectra have been simulated by a Gaussian convolution of peaks (σ = 0.0005 Å) centered at the distance lengths between each Ti atom and other atoms (O or Ti) from its first, second, and third coordination shells. Projections have been constructed by considering only specific titanium atoms with a certain coordination sphere.
Surface areas (SConn) have been evaluated with the algorithm developed by Connolly.56,57 The procedure involves several steps: first, the molecular surface is built from the overlap of all the atomic van der Waals spheres (without considering the few OH groups, which are not considered part of the oxide surface), then a probe sphere (with a chosen radius of 3.0 Å) is rolled on the previously obtained surface, defining a series of contact points. Finally, these points are used to construct arcs that smooth the van der Waals surface, leading to the Connolly surface.
The g(d) distribution function has been calculated by determining the MD-averaged number of water molecules within a distance d and d + Δd away from the nanoparticle surface (Δd = 0.01 Å). The distance d is defined as the minimum value of the distance between the oxygen atom of water (Owater) and the superficial titanium atoms (Tisup). The Tisup species not only include all the undercoordinated titanium atoms (Ti5c, Ti4c, Ti4c(OH), Ti3c(OH)), but also fully coordinated Ti atom (Ti6c_sup) when connected to at least one surface O2c.
To determine the orientation of the water molecules with respect to the surface normal, we evaluated the P(cos θ) probability distribution, where θ is defined as the angle between the radial vector, i.e., the vector that connects the water O to the center of the nanoparticle, and the O–H bond vector. Each point of the P(cos θ) probability distribution is constructed by normalizing the number of times the value of cos θ is between cos θ and cos θ + 0.02 in the MD simulation.
2.4. QM/MM Calculation Setup
The QM/MM calculations have been performed with the Atomic Simulation Environment.58 This toolkit is a driver, which interfaces an internal Explicit Interaction QM/MM scheme59 with external total energy calculators. Specifically, we made use of the DFTB+ software44 for the treatment of the QM part at the DFTB level, whereas for the MM part, composed only of water molecules, we employed the Amber16 code60 with water described by the flexible SPC/Fw model.61 The coupling between the two regions consists of an electrostatic term calculated as the Coulomb interaction between the atomic charges of the QM part and the charges of the MM atoms, whereas all the non-Coulomb interactions (van der Waals) between the subsystems has been implemented as a Lennard-Jones type potential
Values of ϵ and σ for oxygen and hydrogen atoms have been taken from ref (62) where these parameters have been specifically optimized for the interaction between DFTB and a generic force-field, whereas for titanium atoms they have been taken from ref (63).
We employed the same setup described in the previous section for the DFTB calculations. Born–Oppenheimer molecular dynamics (BO-MD) of QM (DFTB) water multilayers around the NS in a shell of MM water molecules have been carried out within the canonical ensemble (NVT). The Newton’s equations of motion were integrated with the velocity Verlet algorithm and a small time step of 1.0 fs ensured reversibility. During MD simulation, a constant temperature of 300 K has been maintained by using the Berendsen thermostat with a time constant of 500 fs. The system has been equilibrated for 5 ps and, then, a production run has been performed for 25 ps.
3. Results and Discussion
3.1. Intrinsic Water on TiO2 Nanospheres
It is experimentally proved that a small quantity of strongly bound water on nanospheres is present up to 600–700 K.4 Thus, this can be considered as “intrinsic” water, being extremely hard to remove. We believe that these molecules are dissociated at very low-coordinated (3- or 4-fold) Ti sites at the surface, which are particularly reactive. Therefore, when modeling a spherical nanoparticle, as in the present study, we must put some dissociated water molecules in the form of hydroxyl (OH) groups to achieve the overall chemical stability of the system. The number of water molecules is assessed according to the following criteria: (1) keep it the least possible and (2) maintain stoichiometry. The model, shown in Figure 1a, is denominated in terms of the number of TiO2 units constituting the nanoparticle and of these intrinsic water molecules: (TiO2)223·10H2O. The distribution of OH groups resulting from the dissociation of the ten water molecules is assessed according to the following criteria: (1) lowest coordination sites first (Ti3c), (2) higher binding sites, (3) no defect states appearing in the band gap. Therefore, the electronic structure of this nanoparticle does not present any peculiar feature, with a band gap of 4.1 eV.
Figure 1.
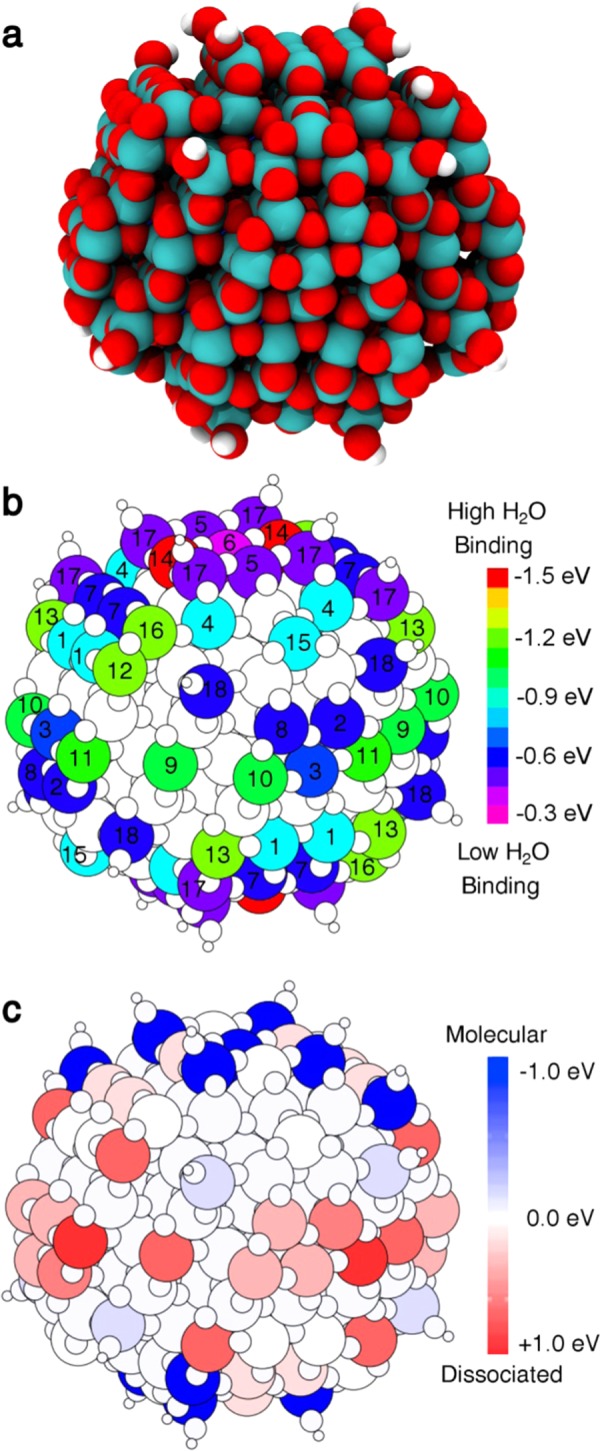
(a) Optimized structure of the NS model in a vacuum (with intrinsic water) as obtained with DFT(B3LYP). Ti atoms are shown in cyan, H atoms in white, and lattice and hydroxyl O atoms in red. (b) Graphical representation of the distribution of binding energies for molecular water molecules on each undercoordinated Ti site of the NS model in a vacuum, as obtained with DFT(B3LYP). The numbering refers to inequivalent Ti undercoordinated sites on the NS surface. (c) Total energy difference between the molecular and dissociative adsorption modes for each Ti site on the surface of the NS model in a vacuum. A positive sign (red color) indicates that the dissociative mode is favored, a negative sign (blue color) indicates that the molecular mode is preferred.
3.2. Single Water Molecule Adsorption on TiO2 Nanospheres
The high ionic character of the Ti–O bond in TiO2 is not sufficient to induce water dissociation on a stoichiometric (101) anatase surface, as it has been well documented in both the experimental and theoretical literature studies.26−29,64,65 We expect that on a curved, highly reactive nanoparticle surface presenting several low-coordinated sites, the situation is different. We have performed a systematic study of the Brønsted–Lowry acidity/basicity for H2O dissociation into OH– on undercoordinated Ti atoms and H+ on bridging O atoms. The competition between molecular (H2O) and dissociated (OH + H) adsorption is mostly governed by the basic strength of the bridging O atom receiving H+.
We observe that, for undissociated water, the range of binding energies goes from −0.3 to about −1.5 eV, as computed at the DFT(B3LYP) level of theory (see Figure 1b). These values are in line with the experimental measurements on round-shaped nanoparticles.5,34 The strongest binding sites are on the north and south poles (top and bottom) of the sphere (site 14), where the surface looks very much like a slightly distorted (001) surface. Then, the other very strong binding sites are located at the equator of the sphere (sites 9, 10, 11) or on the next upper and lower parallel sites (sites 12 and 13). We evaluated the preference for molecular/dissociated water adsorption in terms of energy difference on all sites (Figure 1c). Water is found to favorably dissociate on these Ti sites at the nanosphere equator (e.g., site 11) and on a next upper or lower parallel site (e.g., site 12 or 13).
The corresponding images as in Figure 1b,c, based on the DFTB data, are reported in Figure S1a,b in the Supporting Information. The quantitative comparison between DFT and DFTB binding energies for both molecular and dissociated water molecules is presented through a correlation graph in Figure S2. The molecular water adsorption energies are quite nicely reproduced by DFTB (black bullets), whereas dissociated water adsorption energies are mostly underestimated (red squares). Thus, DFTB tends to excessively favor molecular adsorption in comparison to DFT, which must be seriously taken into account here and in the next sections. Detailed information about water binding energies, as obtained with DFT and DFTB, for the molecular and dissociated adsorption modes on various sites is reported in Table S1.
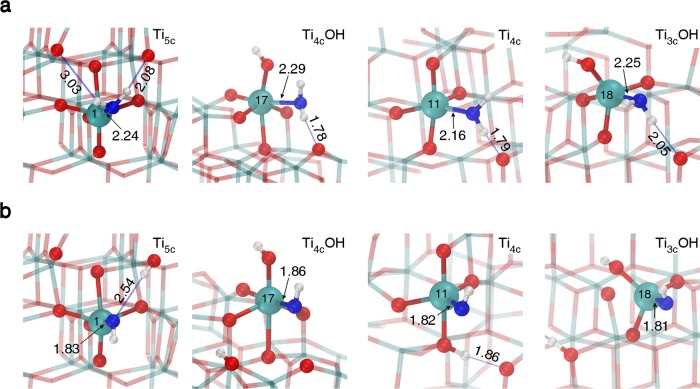
The structural details of a selection of molecular and dissociated water adsorbates are shown in Figure 2 on the 5-fold coordinated Ti sites: Ti5c (1) and Ti4cOH (17), on the 4-fold coordinated Ti site: Ti4c (11) and Ti3cOH (18), as numbered in Figure 1a. Note that other possible adsorption configurations on the nanosphere are shown too, in Figures S3 and S4 of the Supporting Information. We observe that the undissociated water molecules (top row in Figure 2) establish H-bonds with neighboring bridging O atoms in most cases. The Ti–OH2 bond length is between 2.16 and 2.29 Å. This long distance provides some flexibility to the structure, and the water molecules can adjust so as to establish one or two H-bonds. On the contrary, when the water molecule dissociates (bottom row in Figure 2) forming one OH (blue sphere) group and transfers a H to a neighboring bridging O, the Ti–OH bond length is much shorter, ranging from 1.82 to 1.86 Å, which gives much less flexibility to the group that cannot establish H-bonds with neighboring bridging O atoms. We may consider this as “free” OH groups.
Figure 2.
Ball-and-stick representation of a selection (sites 1, 17, 11 and 18) of molecular (a) and dissociated (b) water adsorbates on differently coordinated Ti sites on the surface of the NS model in a vacuum. The adsorption site and its next neighboring atoms are evidenced by larger spheres: Ti atoms are shown in cyan, H atoms in white, lattice and hydroxyl O atoms in red, and water O atoms in blue. The number inside the central Ti atom refers to the numbering in Figure 1b and Table S1. Relevant bond lengths and hydrogen-bonds, shown as thin blue lines, are in Å.
Experimentally, it is possible to characterize free or “H-bonded” OH groups by vibrational spectroscopy since the latter are quite red-shifted (from 3600–3700 to <3000 cm–1).5,39 Our computational DFT vibrational analysis fully agrees with the experimental data in this regard, proving the high level of accuracy and reliability of calculations.
3.3. Water Monolayer Adsorption on TiO2 Nanospheres
Once the mapping of the various sites on the surface was completed, we decorated all adsorption sites on the surface so as to reach full (6-fold) coordination of all Ti ions. This nominal full water monolayer (1 ML) is made up of 134 molecules. The critical issue is to establish the degree of water dissociation on the nanosphere: How much water can really dissociate? What is the global Brønsted–Lowry basicity of the bridging O ions on the nanosphere? How many protons are they willing to accept? To this end, we have investigated different values of the extent of dissociation reaction (α) on the nanosphere, which is defined as follows
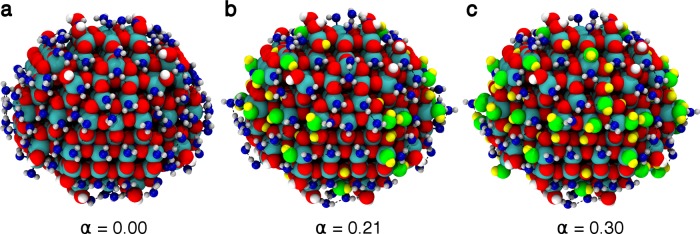
where, nH2O and nOH,H are the number of molecular and dissociated water molecules in the water monolayer, respectively. At the DFT level of theory, we considered: α = 0.0, 0.12, 0.21, and 0.30, as shown in Figures 3 and S5. At the DFTB level of theory it was affordable to consider several other α, as documented in Figure S5. The detailed water adsorption mode distribution on the numerous Ti sites of the surface is listed in Table S2. We observe that the total energy of the system (TiO2 NP + water monolayer) decreases going from α = 0.0 to 0.21 (by −8.48 eV), indicating stabilization due to the dissociation of 28 water molecules on the best dissociation sites. On the contrary, going from α = 0.21 to 0.30, the total energy of the system increases again (by 1.39 eV), indicating that further dissociation of other 12 molecules is not favored. These results are confirmed by the DFTB data that allowed a broader investigation due to the reduced computational cost (Figure S5), considering a higher propensity of DFTB to the molecular adsorption mode, as discussed in Section 3.2. An extent of dissociation reaction of the order of 20%, as estimated by DFT calculations, is in agreement with the experimental evaluation of the amount of OH groups on a spherical nanoparticle determined by titration.40−42
Figure 3.
Optimized structures of the water monolayer with a different extent of dissociation (α) on the NS model, as obtained with DFT(B3LYP): (a) all undissociated (α = 0.00), (b) 28 water molecules out of 134 dissociated (α = 0.21), (c) 40 water molecules out of 134 dissociated (α = 0.30). Titanium, oxygen, and hydrogen atoms of the nanoparticles are shown as cyan, red, and white spheres, respectively. Oxygen atoms from undissociated water molecules are shown in blue. Oxygen and hydrogen atoms of the hydroxyl groups coming from dissociated water molecules are given in green and yellow, respectively.
It is relevant to investigate the effect of the water monolayer on the structural and electronic properties of the spherical TiO2 nanoparticle.
First, we observe a consistent recrystallization of the nanosphere that is evident through the comparison of the simulated EXAFS spectra of bulk anatase, bare, and hydrated (1 ML of water) TiO2 nanosphere, as reported in Figure 4. The broadening of the Ti–O and Ti···Ti peaks is largely reduced upon water adsorption. A similar result has been already reported in a previous molecular mechanics study on the water/TiO2 nanoparticle interface, based on force-field calculations.20 From the experimental point of view, there is an EXAFS report showing that enediol ligand adsorption on spherical nanoparticles results in partial restoration of the octahedral Ti coordination environment and restructuring of the nanoparticle surface,35 in line with our findings. Similarly, ZnS nanoparticle recrystallization in water has been observed.66 It is extremely interesting to note that this effect is totally absent in faceted nanoparticles, where water adsorption does not alter the crystallite ordering. In parallel to consistent recrystallization, we also observe a large surface energy reduction upon hydration that makes the spherical nanoparticles competitive with faceted ones. In a vacuum, faceted nanoparticle surface energy is lower than that for nanospheres (0.59 vs 0.72 J/m2), since the former expose highly stable (101) facets. These values are in excellent agreement with the experimental ones.37 Upon water adsorption, the relative stability is reversed: nanospheres are more stabilized by water than faceted nanoparticles, resulting in a more negative surface energy (−0.13 vs −0.04 J/m2). In other words, we provide computational evidence that, in the presence of water molecules, spherical TiO2 nanoparticles would be more stable than faceted nanoparticles. A predominant effect of a water layer on the relative stability of different surface structures was recently proven in the case of rutile (011) surface by a combined experimental/theoretical study,3 where the presence of water causes deconstruction into the bulk-terminated (1 × 1) surface. Note that a negative surface energy implies that the surface is more stable than the bulk phase. This is not realistic for a single component system, e.g., pure TiO2. However, in the case of multicomponent systems, e.g., TiO2/water, this is feasible, as demonstrated by Selloni et al.67 for anatase TiO2 surfaces and by Nørskov et al.68 for alumina surfaces in aqueous surroundings.
Figure 4.
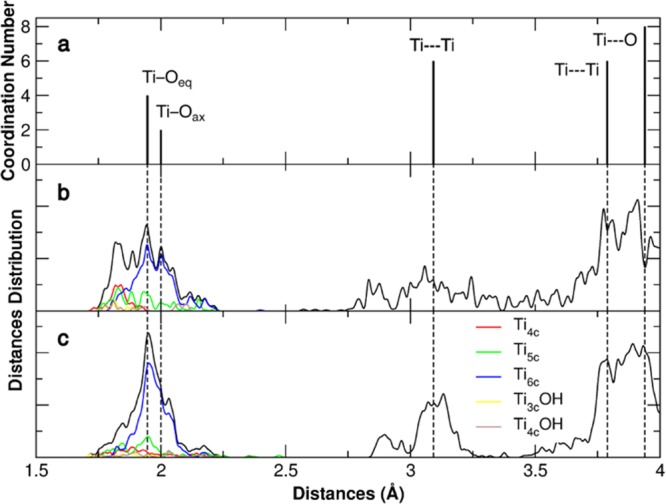
Simulated EXAFS spectra computed with DFT(B3LYP) for the anatase bulk (a) and for the NS model in a vacuum (b) and with a water monolayer (α = 0.21) adsorbed (c). The total distribution of Ti–O, Ti···Ti, and Ti···O distances is reported in black, whereas the distribution of the same distances for each type of Ti is color-coded according to their coordination pattern.
The effect of water adsorption on the electronic structure of TiO2 nanoparticles is analyzed in terms of comparison of the density of states (DOS) for the nanosphere in a vacuum with that for the hydrated nanospheres (at a different degree of dissociation, α = 0.0, 0.21, and 0.30), as reported in Figure 5. We observe that the presence of an adsorbing water monolayer upshifts the top of the valence band, and thus reduces the work function of the system (Figure 5a vs 5b–d). This effect is most pronounced (+1.32 eV) when all the water molecules on the surface are undissociated (Figure 5b), because of the dipole orientation of the water molecules. It reduces slightly and progressively with the water dissociation degree to +0.97 and to +0.89 eV, respectively (see Figure 5c,d). The experimental shift of the valence band due to solvation can be obtained from the difference between band positions by photoemission experiments and by electrochemical measurements, as discussed in detail in ref (69) for rutile TiO2. Considering UPS,70 flat-band potential,71 and potential of zero charge36 data available for anatase TiO2, we could determine the experimental estimate of the solvation shift to be +1.51 eV, in fair agreement with our theoretical values above.
Figure 5.
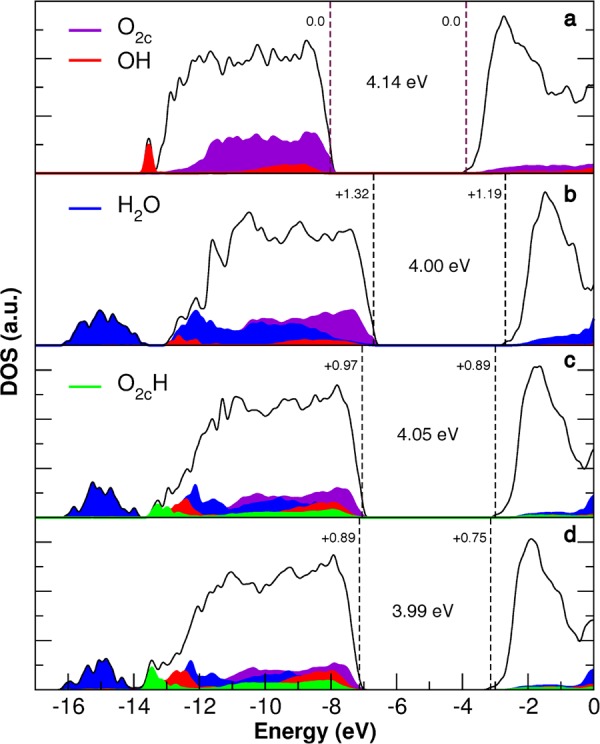
Total (DOS) and projected density of states on different oxygen species (a) of the NS in a vacuum, (b) of the NS with a monolayer of molecular water (α = 0.00) and (c) and (d) with a monolayer in which a portion of water is dissociated (α = 0.21, α = 0.30, respectively). In each panel, the band gap and the energy shift of the valence and conduction band edges with respect to the NS model in a vacuum are given in eV. A 0.005 eV Gaussian broadening was used. The zero energy is set to the vacuum level.
3.4. Water Multilayer Adsorption on TiO2 Nanospheres
On top of the water monolayer on the TiO2 nanosphere, at increasing water partial pressure, further water layers adsorb up to an extent where the nanoparticle is completely immersed in an aqueous medium, which will be discussed in the next section. Here, we present a dynamic investigation of a multilayer of water up to a thickness of about 1 nm, as shown in Figure 6a.
Figure 6.
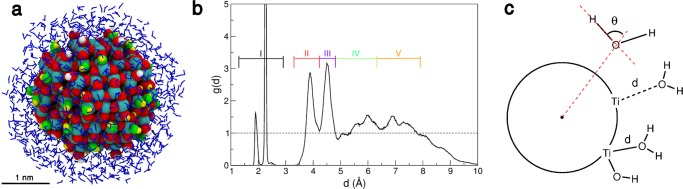
(a) Snapshot of the final structure from the DFTB molecular dynamics run of the NS model with a water multilayer, i.e., a monolayer of water (α = 0.21) and an additional spherical shell of 824 H2O molecules, resulting in an overall stoichiometry of (TiO2)223·958H2O. Titanium, oxygen, and hydrogen atoms of the nanoparticles are shown as cyan, red, and white spheres, respectively; oxygen and hydrogen atoms of hydroxyl groups coming from dissociated water molecules are given in green and yellow, respectively; undissociated water molecules are shown as blue sticks. (b) Distribution function g(d) as extracted from the DFTB molecular dynamics run on the water multilayer. Roman numbers from I to V indicate the different water layers. A dashed black line is traced for g(d) = 1, which corresponds to bulk water density. (c) Schematic representation of the distance d, i.e., the minimum distance between the oxygen of the water molecule and surface titanium atoms of the NS and of the angle θ, i.e., the angle between the O–H bond vector and the vector connecting the water oxygen atom with the center of the NS model.
We analyzed the results of the DFTB-based molecular dynamics (45 ps) by plotting the distribution function g(d) (Figure 6b), where d is defined as the distance of the water O atom from the closest surface Ti atom (see Figure 6c for a schematic representation). We observe four distinct peaks (two peaks in layer I, one peak in layer II, and one peak in layer III) and two broader features that we will assign to layer IV and layer V (Figure 6b). Various layers are sketched in different colors in Figure 7a: layer I in black is made up of OH groups or H2O molecules that are directly bound to surface Ti atoms through the Owater atom; layer II in red is made up of H2O molecules that are H-bonded to surface O atoms or to Ti–OH groups through the Hwater atoms; layer III in violet is made up of H2O molecules that are H-bonded to Ti–OH groups or Ti–OH2 through the Owater atom; layers IV–V in green and orange are made up of H2O molecules that are H-bonded to those in the lower layers both through Hwater and Owater atoms. However, the g(d) distribution function may be overstructured between 5 and 7 Å from the surface due to the limitation of the model. The behavior of water in this range will be further discussed in the next section, in which we considered the presence of outer layers.
Figure 7.
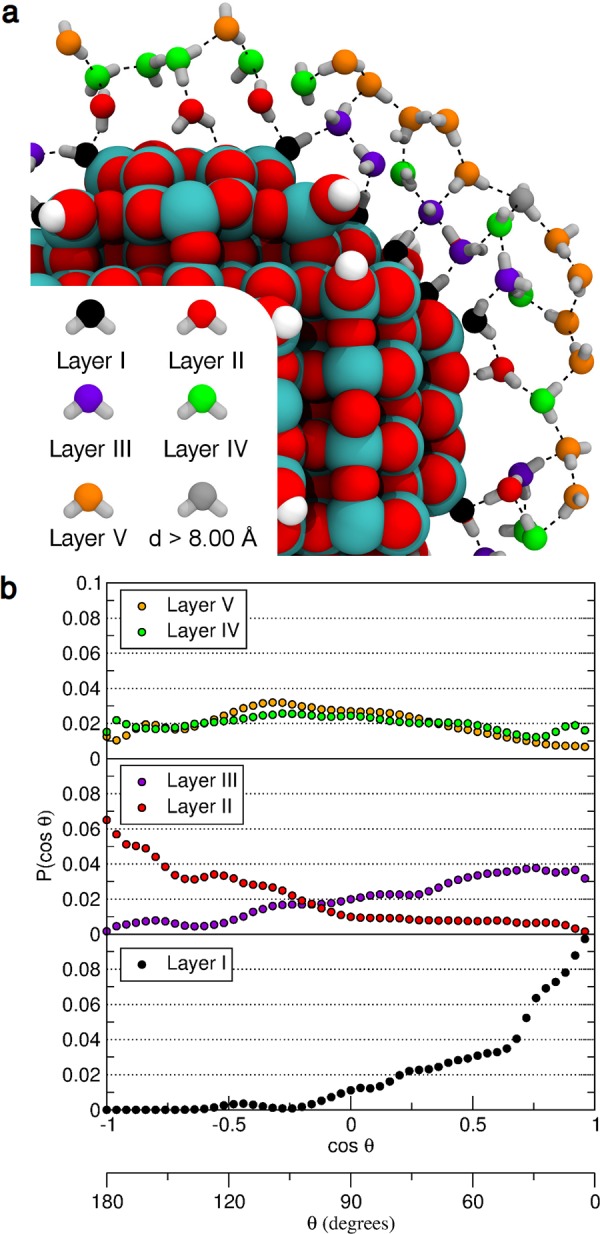
(a) Top view of the cross-section of the water multilayer on the NS model, as obtained from the last snapshot of the DFTB molecular dynamics simulation. Oxygen atoms of the adsorbed water molecules and OH groups are color-coded according to their distance from the closest titanium atom. Titanium, oxygen, and hydrogen atoms of the nanoparticle are shown as cyan, red, and white spheres, respectively. Hydrogen bonds are represented as dashed black lines. (b) Probability distribution P(cos θ) of the angle θ between the O–H bond vector and the vector connecting water O atom to the center of the NS model for the molecules of the water multilayer adsorbed on the NS model within layer I (bottom panel, in black), Layers II and III (as red and violet points, respectively, in the middle panel) and layers IV and V (as green and orange points, respectively, in the top panel). cos θ equals to 1 means that the O–H bond is directed outwards, whereas a value close to −1 means that the O–H bond is oriented toward the center of the nanosphere.
It is relevant to monitor the degree of order in the orientation of water molecules in different layers. In Figure 7b, we plot the probability distribution function of the θ angle (defined in Figure 6c). When θ is above 90°, the OH bond is oriented toward the center of the nanoparticle, whereas when θ is below 90° the OH bond is oriented toward the vacuum. Thus, we infer that layer I of water points toward the vacuum, layer II points mainly toward the nanoparticle, layer III mostly points toward the vacuum, whereas for layers IV and V there is no preferred directionality but the water molecules are rather randomly oriented with all possible θ values represented in the distribution function. This analysis is corroborated by the evaluation of the radial component of the dipole moment for each water layer averaged with respect to all the water molecules contained in that layer and with respect to all the configurations along the simulation run: for layer II it is −2.91 D/molecule, for layer III it is +2.50 D/molecule and for layer IV it is −0.50 D/molecule. This was not done for layer I because it involves covalent bonding with surface atoms and for layer V because it is in contact with the vacuum.
Vibrational sum frequency generation (SFG) spectroscopy performed on spherical anatase TiO2 nanoparticles confirms that the physisorbed water layer below 4 Å (layer II) points toward the nanoparticle.38 Additionally, this vibrational study reveals that the chemisorbed layer is a H-bond donor, resulting in a rather large red-shifted OH vibrational frequency (with respect to “free OH”), in line with another study by Shirai et al.5
3.5. TiO2 Nanospheres in an Aqueous Medium
Finally, the behavior of the TiO2 nanosphere in a more realistic aqueous environment has been investigated. To study outer solvation shells, we made use of a series of QM/MM calculations, where the QM part has been treated at a DFTB level of theory, whereas the MM part has been modeled with the flexible water model SPC/Fw.61 We performed two QM/MM calculations, which differ for the portion of the system described at the QM level: in the first one, the QM region is composed of the NS and a surrounding 0.5 nm thick water multilayer, which are immersed in a 8 nm-wide MM water droplet; in the second one the QM region is extended up to 1 nm from the NS surface and again it is immersed in a 8 nm-wide MM water droplet (see Figure 8a). In other words, in the former case, labeled as “DFTB 3L + MM”, only layers I, II, and III, as defined in Section 3.4, have been considered in the QM part, whereas in the latter case, labeled “DFTB 5L + MM”, all the NS + water system of Section 3.4 (see Figure 6a) has been treated at the QM level of theory.
Figure 8.
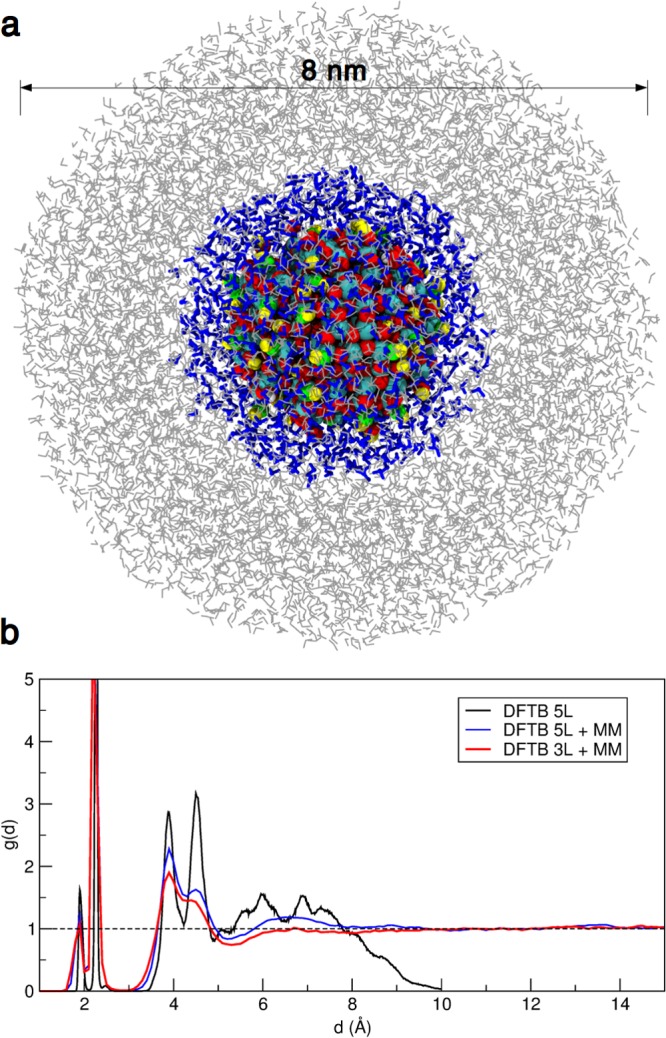
(a) Representation of the NS model with a water multilayer (in blue) enclosed in a water droplet (in gray), resulting in an overall stoichiometry of (TiO2)223·8958H2O. Titanium, oxygen, and hydrogen atoms of the nanoparticle are shown as cyan, red, and white spheres, respectively; oxygen and hydrogen atoms of hydroxyl groups coming from dissociated water molecules are given in green and yellow, respectively; undissociated water molecules of the multilayer (treated at the DFTB level of theory) are shown with blue sticks, whereas the rest of the water (treated at the MM level of theory) is represented by gray lines. (b) Distribution function g(d) as extracted from the QM(DFTB)/MM molecular dynamics runs of the water multilayer (for definition of 3L and 5L see text) on the NS model in an 8 nm water droplet.
The QM/MM molecular dynamics runs (30 ns) have been analyzed in terms of the g(d) distribution function (Figure 8b). Considering the multilayer surrounded by MM water (blue curve), we note that layers IV and V from the DFTB-only calculation (DFTB 5L, black curve) merged to give a single broad peak in the blue line for DFTB 5L + MM. This is a clear indication that the observed excessive layering from 5 to 7 Å, discussed in the previous section, is due to the limited size of the model rather than to a real physical feature. Comparing now the DFTB 5L + MM with the DFTB 3L + MM molecular dynamics, where the QM region is limited to layers I, II, and III, we can conclude that the QM level of theory is crucial in the description of the water distribution between 5 and 7 Å. In fact, in DFTB 3L + MM no peak is observed for distances larger than those included in the QM region, meaning that molecular mechanics is not able to reproduce the increase in the density of water at around 6 Å from the NS surface. Some long-range effect on water structuring has been previously reported for the (100) TiO2 anatase surface by ab initio molecular dynamics.72 However, in this case, periodic boundary conditions could have introduced spurious effects due to the limited volume available for the solvent and due to the potential of the repeated slab surface.72
Another relevant difference with the DFTB-only calculation (DFTB 5L in Figure 8b) is the decrease in the density of the second and, even more dramatically, of the third layer in the g(d) distance distribution. We assign this to a screening effect, weakening the Coulombic interaction and hence the water H-bonds with the NS surface oxygen species. Consequently, the formation of dense and compressed solvation layers in close contact to the nanoparticle is disfavored.
Analogous to Section 3.4, we analyze the water molecule orientation in I, II, III and the merged IV + V solvation layers, as averaged along the DFTB 5L + MM molecular dynamics (see Figure S6 in the Supporting Information). The probability distribution of cos θ in different layers is very similar to the one already discussed for the multilayer in Section 3.4. In particular, it is even clearer here that the merged IV + V water layers are composed of randomly oriented molecules and the presence of the nanoparticle only causes an increase in the density with respect to bulk water between about 5 and 7 Å.
From this analysis, we conclude that not only water affects the NS properties, but also that the NS influences the surrounding water up to a distance of 1 nm from the surface. Moreover, if one could further extend the QM region, we expect that some more density peaks in the water distribution function g(d) may appear at longer distances (above 8 Å), due to a long-range effect of the NS on water structuring.
4. Conclusions
In this work, we presented a multistep and multiscale investigation based on DFT, DFTB, and QM(DFTB)/MM calculations. Increasing water partial pressure conditions were considered.
At the DFT level of theory, we investigated single water molecule adsorption modes on various types of uncoordinated sites present on a realistic curved nanoparticle (700 atoms). Water is found to favorably dissociate, mostly on the undercoordinated Ti sites at the equator of the sphere, in contrast to what is observed on flat (101) surfaces in faceted nanocrystals. Dissociated OH groups cannot form H-bonds with surface oxygens (free OH), whereas molecularly adsorbed water does.
Then, by decorating all the adsorption sites, we studied the full water monolayer coverage (134 H2O molecules). We observed large nanoparticle recrystallization by simulating the EXAFS spectrum. This largely reduces the surface energy, so that we observe a stability inversion with respect to faceted nanoparticles. We also determined that the optimal extent of water dissociation, defined as the number of dissociated water out of the total number of adsorbed water molecules, is around 20% (α = 0.2). Nanoparticle work function is rather altered by the presence of a water monolayer shifting by about 1 eV.
At increasing water partial pressure, further layers are expected to add to the surface. At the DFTB level of theory, we considered water multilayer adsorption up to a thickness of 1 nm (134+824=958 H2O molecules) and performed molecular dynamics simulations, which evidenced layer structuring and molecular orientation around the curved nanoparticle. Five water layers were identified by analyzing the distribution function of water distances from the surface. In layer I, molecules point toward the vacuum, in layer II toward the nanoparticle, in layer III toward the vacuum again, and then no preferential directionality could be identified.
We clarified whether these effects arise as a consequence of tension at the water drop surface around the nanosphere by simulating a bulk water up to a distance of 3 nm from the oxide surface with the QM(DFTB)/MM approach (958 (QM) + 8000 (MM) = 8958 H2O molecules). We proved that the nanoparticle/water interaction goes rather long range since the dipole orientation of water molecules is confirmed and observed up to a distance of 5 Å, whereas water structuring extends at least up to a distance of 8 Å from the surface.
To conclude, with this work we provided a very detailed and accurate description, mostly at a quantum mechanical level, of TiO2 spherical nanoparticle interaction with water, starting from the short-range (chemical) adsorption at low water partial pressure, increasing it through water multilayers adsorption, up to a bulk water environment, with a QM/MM approach, where long-range (physical) effects clearly emerge.
Acknowledgments
The authors are grateful to Asmus Ougaard Dohn at Iceland University and Jens Jørgen Mortensen at DTU for fruitful discussions. The project has received funding from the European Research Council (ERC) under the European Union’s HORIZON2020 research and innovation program (ERC Grant Agreement No [647020]).
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.8b08172.
Graphical representation of DFTB binding energy distribution for molecular and dissociated water, correlation of DFTB/DFT binding energies for molecular and dissociated water, representation of molecular and dissociated water adsorption configurations, binding energy of a water monolayer as a function of the extent of dissociation α for DFT and DFTB, probability distribution P(cos θ) for the QM/MM MD simulation, tabulated binding energies for molecular and dissociated water molecules as obtained with DFT and DFTB, composition of water adsorbates in monolayers with a different extent of dissociation (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Diebold U. Perspective: A Controversial Benchmark System for Water-oxide Interfaces: H2O/TiO2(110). J. Chem. Phys. 2017, 147, 040901 10.1063/1.4996116. [DOI] [PubMed] [Google Scholar]
- Mu R.; Zhao Z.-j.; Dohnálek Z.; Gong J. Structural Motifs of Water on Metal Oxide Surfaces. Chem. Soc. Rev. 2017, 46, 1785–1806. 10.1039/C6CS00864J. [DOI] [PubMed] [Google Scholar]
- Balajka J.; Aschauer U.; Mertens S. F. L.; Selloni A.; Schmid M.; Diebold U. Surface Structure of TiO2 Rutile (011) Exposed to Liquid Water. J. Phys. Chem. C 2017, 121, 26424–26431. 10.1021/acs.jpcc.7b09674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirai K.; Sugimoto T.; Watanabe K.; Haruta M.; Kurata H.; Matsumoto Y. Effect of Water Adsorption on Carrier Trapping Dynamics at the Surface of Anatase TiO2 Nanoparticles. Nano Lett. 2016, 16, 1323–1327. 10.1021/acs.nanolett.5b04724. [DOI] [PubMed] [Google Scholar]
- Shirai K.; Fazio G.; Sugimoto T.; Selli D.; Ferraro L.; Watanabe K.; Haruta M.; Ohtani B.; Kurata H.; Di Valentin C.; Matsumoto Y. Water-Assisted Hole Trapping at Highly Curved Surface of Nano-TiO2 Photocatalyst. J. Am. Chem. Soc. 2018, 140, 1415–1422. 10.1021/jacs.7b11061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tilocca A.; Selloni A. Vertical and Lateral Order in Adsorbed Water Layers on Anatase TiO2(101). Langmuir 2004, 20, 8379–8384. 10.1021/la048937r. [DOI] [PubMed] [Google Scholar]
- Tilocca A.; Selloni A. DFT-GGA and DFT+U Simulations of Thin Water Layers on Reduced TiO2 Anatase. J. Phys. Chem. C 2012, 116, 9114–9121. 10.1021/jp301624v. [DOI] [Google Scholar]
- Aschauer U. J.; Tilocca A.; Selloni A. Ab Initio Simulations of the Structure of Thin Water Layers on Defective Anatase TiO2 (101) Surfaces. Int. J. Quantum Chem. 2015, 115, 1250–1257. 10.1002/qua.24918. [DOI] [Google Scholar]
- Cheng J.; Sprik M. The Electric Double Layer at a Rutile TiO2 Water Interface Modelled Using Density Functional Theory Based Molecular Dynamics Simulation. J. Phys.: Condens. Matter 2014, 26, 244108 10.1088/0953-8984/26/24/244108. [DOI] [PubMed] [Google Scholar]
- Colombo D. P. Jr.; Roussel K. A.; Saeh J.; Skinner D. E.; Cavaleri J. J.; Bowman R. M. Femtosecond Study of the Intensity Dependence of Electron-Hole Dynamics in TiO2 Nanoclusters. Chem. Phys. Lett. 1995, 232, 207–214. 10.1016/0009-2614(94)01343-T. [DOI] [Google Scholar]
- Serpone N.; Lawless D.; Khairutdinov R. Size Effects on the Photophysical Properties of Colloidal Anatase TiO2 Particles: Size Quantization or Direct Transitions in This Indirect Semiconductor?. J. Phys. Chem. 1995, 99, 16646–16654. 10.1021/j100045a026. [DOI] [Google Scholar]
- Liu Y.; Claus R. O. Blue Light Emitting Nanosized TiO2 Colloids. J. Am. Chem. Soc. 1997, 119, 5273–5274. 10.1021/ja970587q. [DOI] [Google Scholar]
- Micic O. I.; Zhang Y.; Cromack K. R.; Trifunac A. D.; Thurnauer M. C. Trapped Holes on Titania Colloids Studied by Electron Paramagnetic Resonance. J. Phys. Chem. 1993, 97, 7277–7283. 10.1021/j100130a026. [DOI] [Google Scholar]
- Luca V. Comparison of Size-Dependent Structural and Electronic Properties of Anatase and Rutile Nanoparticles. J. Phys. Chem. C 2009, 113, 6367–6380. 10.1021/jp808358v. [DOI] [Google Scholar]
- Dimitrijevic N. M.; Saponjic Z. V.; Rabatic B. M.; Poluektov O. G.; Rajh T. Effect of Size and Shape of Nanocrystalline TiO2 on Photogenerated Charges. An EPR Study. J. Phys. Chem. C 2007, 111, 14597–14601. 10.1021/jp0756395. [DOI] [Google Scholar]
- Nilsson A.; Pettersson L. G. M. Perspective on the Structure of Liquid Water. Chem. Phys. 2011, 389, 1–34. 10.1016/j.chemphys.2011.07.021. [DOI] [Google Scholar]
- Nilsson A.; Pettersson L. G. M. The Structural Origin of Anomalous Properties of Liquid Water. Nat. Commun. 2015, 6, 8998 10.1038/ncomms9998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gillan M. J.; Alfè D.; Michaelides A. Perspective: How Good is DFT for Water?. J. Chem. Phys. 2016, 144, 130901 10.1063/1.4944633. [DOI] [PubMed] [Google Scholar]
- Schnur S.; Groß A. Properties of Metal–Water Interfaces Studied from First Principles. New J. Phys. 2009, 11, 125003 10.1088/1367-2630/11/12/125003. [DOI] [Google Scholar]
- Koparde V. N.; Cummings P. T. Molecular Dynamics Study of Water Adsorption on TiO2 Nanoparticles. J. Phys. Chem. C 2007, 111, 6920–6926. 10.1021/jp0666380. [DOI] [Google Scholar]
- Kim S.-Y.; van Duin A. C. T.; Kubicki J. D. Molecular Dynamics Simulations of the Interactions between TiO2 Nanoparticles and Water with Na+ and Cl–, Methanol, and Formic Acid using a Reactive Force Field. J. Mater. Res. 2013, 28, 513–520. 10.1557/jmr.2012.367. [DOI] [Google Scholar]
- Liu S.; Meng X.-Y.; Perez-Aguilar J. M.; Zhou R. An In Silico study of TiO2 Nanoparticles Interaction with Twenty Standard Amino Acids in Aqueous Solution. Sci. Rep. 2016, 6, 37761 10.1038/srep37761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumita M.; Hu C.; Tateyama Y. Interface Water on TiO2 Anatase (101) and (001) Surfaces: First-Principles Study with TiO2 Slabs Dipped in Bulk Water. J. Phys. Chem. C 2010, 114, 18529–18537. 10.1021/jp105364z. [DOI] [Google Scholar]
- Tilocca A.; Selloni A. Structure and Reactivity of Water Layers on Defect-Free and Defective Anatase TiO2(101) Surfaces. J. Phys. Chem. B 2004, 108, 4743–4751. 10.1021/jp037685k. [DOI] [Google Scholar]
- Vittadini A.; Casarin M.; Selloni A. Chemistry of and on TiO2-Anatase Surfaces by DFT Calculations: a Partial Review. Theor. Chem. Acc. 2007, 117, 663–671. 10.1007/s00214-006-0191-4. [DOI] [Google Scholar]
- Vittadini A.; Selloni A.; Rotzinger F. P.; Grätzel M. Structure and Energetics of Water Adsorbed at TiO2 Anatase (101) and (001) Surfaces. Phys. Rev. Lett. 1998, 81, 2954–2957. 10.1103/PhysRevLett.81.2954. [DOI] [Google Scholar]
- De Angelis F.; Di Valentin C.; Fantacci S.; Vittadini A.; Selloni A. Theoretical Studies on Anatase and Less Common TiO2 Phases: Bulk, Surfaces, and Nanomaterials. Chem. Rev. 2014, 114, 9708–9753. 10.1021/cr500055q. [DOI] [PubMed] [Google Scholar]
- Herman G. S.; Dohnàlek Z.; Ruzycki N.; Diebold U. Experimental Investigation of the Interaction of Water and Methanol with Anatase-TiO2(101). J. Phys. Chem. B 2003, 107, 2788–2795. 10.1021/jp0275544. [DOI] [Google Scholar]
- He Y.; Tilocca A.; Dulub O.; Selloni A.; Diebold U. Local Ordering and Electronic Signature of Submonolayer Water on Anatase TiO2 (101). Nat. Mater. 2009, 8, 585–589. 10.1038/nmat2466. [DOI] [PubMed] [Google Scholar]
- Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
- Becke A. D. Density-functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. 10.1063/1.464913. [DOI] [Google Scholar]
- Elstner M.; Porezag D.; Jungnickel G.; Elsner J.; Haugk M.; Frauenheim T.; Suhai S.; Seifert G. Self-Consistent-Charge Density-Functional Tight-Binding Method for Simulations of Complex Materials Properties. Phys. Rev. B 1998, 58, 7260–7268. 10.1103/PhysRevB.58.7260. [DOI] [Google Scholar]
- Benkoula S.; Sublemontier O.; Patanen M.; Nicolas C.; Sirotti F.; Naitabdi A.; Gaie-Levrel F.; Antonsson E.; Aureau D.; Ouf F.-X.; Wada S.-I.; Etcheberry A.; Ueda K.; Miron C. Water Adsorption on TiO2 Surfaces Probed by Soft X-Ray Spectroscopies: Bulk Materials vs Isolated Nanoparticles. Sci. Rep. 2015, 5, 15088 10.1038/srep15088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li G.; Li L.; Boerio-Goates J.; Woodfield B. F. High Purity Anatase TiO2 Nanocrystals: Near Room-Temperature Synthesis, Grain Growth Kinetics, and Surface Hydration Chemistry. J. Am. Chem. Soc. 2005, 127, 8659–8666. 10.1021/ja050517g. [DOI] [PubMed] [Google Scholar]
- Rajh T.; Chen L. X.; Lukas K.; Liu T.; Thurnauer M. C.; Tiede D. M. Surface Restructuring of Nanoparticles: An Efficient Route for Ligand–Metal Oxide Crosstalk. J. Phys. Chem. B 2002, 106, 10543–10552. 10.1021/jp021235v. [DOI] [Google Scholar]
- Nosaka A. Y.; Fujiwara T.; Yagi H.; Akutsu H.; Nosaka Y. Characteristics of Water Adsorbed on TiO2 Photocatalytic Systems with Increasing Temperature as Studied by Solid-State 1H-NMR Spectroscopy. J. Phys. Chem. B 2004, 108, 9121–9125. 10.1021/jp037297i. [DOI] [Google Scholar]
- Levchenko A. A.; Li G.; Boerio-Goates J.; Woodfield B. F.; Navrotsky A. TiO2 Stability Landscape: Polymorphism, Surface Energy, and Bound Water Energetics. Chem. Mater. 2006, 18, 6324–6332. 10.1021/cm061183c. [DOI] [Google Scholar]
- Hosseinpour S.; Tang F.; Wang F.; Livingstone R. A.; Schlegel S. J.; Ohto T.; Bonn M.; Nagata Y.; Backus E. H. G. Chemisorbed and Physisorbed Water at the TiO2/Water Interface. J. Phys. Chem. Lett. 2017, 8, 2195–2199. 10.1021/acs.jpclett.7b00564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.-y.; Groenzin H.; Shultz M. J. Molecular Species on Nanoparticulate Anatase TiO2 Film Detected by Sum Frequency Generation: Trace Hydrocarbons and Hydroxyl Groups. Langmuir 2003, 19, 7330–7334. 10.1021/la0345542. [DOI] [Google Scholar]
- Bahnemann D. W.; Hilgendorff M.; Memming R. Charge Carrier Dynamics at TiO2 Particles: Reactivity of Free and Trapped Holes. J. Phys. Chem. B 1997, 101, 4265–4275. 10.1021/jp9639915. [DOI] [Google Scholar]
- Herrmann M.; Kazula U.; Boehm H. P. Über die Chemie der Oberfläche des Titandioxids. IV. Austausch von Hydroxidionen gegen Fluoridionen. Z. Anorg. Allg. Chem. 1970, 372, 308–313. 10.1002/zaac.19703720307. [DOI] [Google Scholar]
- Flaig-Baumann R.; Herrmann M.; Boehm H. P. Über die Chemie der Oberfläche des Titandioxids. III. Reaktionen der Basischen Hydroxylgruppen auf der Oberfläche. Z. Anorg. Allg. Chem. 1970, 372, 296–307. 10.1002/zaac.19703720306. [DOI] [Google Scholar]
- Dovesi R.; Saunders V. R.; Roetti C.; Orlando R.; Zicovich-Wilson C. M.; Pascale F.; Civalleri B.; Doll K.; Harrison N. M.; Bush I. J.; D’Arco P.; Llunell M.; Causà M.; Noël Y.. CRYSTAL14 User’s Manual; University of Torino: Torino, 2014.
- Aradi B.; Hourahine B.; Frauenheim T. DFTB+, a Sparse Matrix-Based Implementation of the DFTB Method. J. Phys. Chem. A 2007, 111, 5678–5684. 10.1021/jp070186p. [DOI] [PubMed] [Google Scholar]
- Fox H.; Newman K. E.; Schneider W. F.; Corcelli S. A. Bulk and Surface Properties of Rutile TiO2 from Self-Consistent-Charge Density Functional Tight Binding. J. Chem. Theory Comput. 2010, 6, 499–507. 10.1021/ct900665a. [DOI] [PubMed] [Google Scholar]
- Fuertes V. C.; Negre C. F. A.; Oviedo M. B.; Bonafé F. P.; Oliva F. Y.; Sánchez C. G. A Theoretical Study of the Optical Properties of Nanostructured TiO2. J. Phys.: Condens. Matter 2013, 25, 115304 10.1088/0953-8984/25/11/115304. [DOI] [PubMed] [Google Scholar]
- Dolgonos G.; Aradi B.; Moreira N. H.; Frauenheim T. An Improved Self-Consistent-Charge Density-Functional Tight-Binding (SCC-DFTB) Set of Parameters for Simulation of Bulk and Molecular Systems Involving Titanium. J. Chem. Theory Comput. 2010, 6, 266–278. 10.1021/ct900422c. [DOI] [PubMed] [Google Scholar]
- Elstner M.; Seifert G. Density Functional Tight Binding. Philos. Trans. R. Soc., A 2014, 372, 20120483 10.1098/rsta.2012.0483. [DOI] [PubMed] [Google Scholar]
- Seifert G.; Joswig J.-O. Density-functional Tight Binding—an Approximate Density-Functional Theory Method. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2, 456–465. 10.1002/wcms.1094. [DOI] [Google Scholar]
- Selli D.; Fazio G.; Seifert G.; Di Valentin C. Water Multilayers on TiO2 (101) Anatase Surface: Assessment of a. J. Chem. Theory Comput. 2017, 13, 3862–3873. 10.1021/acs.jctc.7b00479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luschtinetz R.; Frenzel J.; Milek T.; Seifert G. Adsorption of Phosphonic Acid at the TiO2 Anatase (101) and Rutile (110) Surface. J. Phys. Chem. C 2009, 113, 5730–5740. 10.1021/jp8110343. [DOI] [Google Scholar]
- Hu H.; Lu Z.; Elstner M.; Hermans J.; Yang W. Simulating Water with the Self-Consistent-Charge Density Functional Tight Binding Method: From Molecular Clusters to the Liquid State. J. Phys. Chem. A 2007, 111, 5685–5691. 10.1021/jp070308d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selli D.; Fazio G.; Di Valentin C. Modelling Realistic TiO2 Nanospheres: A Benchmark Study of SCC-DFTB against DFT. J. Chem. Phys. 2017, 147, 164701 10.1063/1.4994165. [DOI] [PubMed] [Google Scholar]
- Fazio G.; Ferrighi L.; Di Valentin C. Spherical versus Faceted Anatase TiO2 Nanoparticles: A Model Study of Structural and Electronic Properties. J. Phys. Chem. C 2015, 119, 20735–20746. 10.1021/acs.jpcc.5b06384. [DOI] [Google Scholar]
- Martínez L.; Andrade R.; Birgin E. G.; Martinez J. M. PACKMOL: A Package for Building Initial Configurations for Molecular Dynamics Simulations. J. Comput. Chem. 2009, 30, 2157–2164. 10.1002/jcc.21224. [DOI] [PubMed] [Google Scholar]
- Connolly M. L. Analytical Molecular Surface Calculation. J. Appl. Crystallogr. 1983, 16, 548–558. 10.1107/S0021889883010985. [DOI] [Google Scholar]
- Connolly M. L. Solvent-Accessible Surfaces of Proteins and Nucleic Acids. Science 1983, 221, 709–713. 10.1126/science.6879170. [DOI] [PubMed] [Google Scholar]
- Larsen A. H.; Mortensen J. J.; Blomqvist J.; Castelli I. E.; Christensen R.; Dułak M.; Friis J.; Groves M. N.; Hammer B.; Hargus C.; Hermes E. D.; Jennings P. C.; Jensen P. B.; Kermode J.; Kitchin J. R.; Kolsbjerg E. L.; Kubal J.; Kaasbjerg K.; Lysgaard S.; Bergmann Maronsson J.; Maxson T.; Olsen T.; Pastewka L.; Peterson A.; Rostgaard C.; Schiøtz J.; Schütt O.; Strange M.; Thygesen K. S.; Vegge T.; Vilhelmsen L.; Walter M.; Zeng Z.; Jacobsen K. W. The Atomic Simulation Environment—a Python Library for Working with Atoms. J. Phys.: Condens. Matter 2017, 29, 273002 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
- Dohn A. O.; Jónsson E. Ö; Levi G.; Mortensen J. J.; Lopez-Acevedo O.; Thygesen K. S.; Jacobsen K. W.; Ulstrup J.; Henriksen N. E.; Møller K. B.; Jónsson H. Grid-Based Projector Augmented Wave (GPAW) Implementation of Quantum Mechanics/Molecular Mechanics (QM/MM) Electrostatic Embedding and Application to a Solvated Diplatinum Complex. J. Chem. Theory. Comput. 2017, 13, 6010–6022. 10.1021/acs.jctc.7b00621. [DOI] [PubMed] [Google Scholar]
- Case D. A.; Cerutti D. S.; Cheatham T. E. III; Darden T. A.; Duke R. E.; Giese T. J.; Gohlke H.; Goetz A. W.; Greene D.; Homeyer N.; Izadi S.; Kovalenko A.; Lee T. S.; LeGrand S.; Li P.; Lin C.; Liu J.; Luchko T.; Luo R.; Mermelstein D.; Merz K. M.; Monard G.; Nguyen H.; Omelyan I.; Onufriev A.; Pan F.; Qi R.; Roe D. R.; Roitberg A.; Sagui C.; Simmerling C. L.; Botello-Smith W. M.; Swails J.; Walker R. C.; Wang J.; Wolf R. M.; Wu X.; Xiao L.; York D. M.; Kollman P. A.. AMBER 2017; University of California: San Francisco, 2017.
- Paesani F.; Zhang W.; Case D. A.; Cheatham T. E.; Voth G. A. An Accurate and Simple Quantum Model for Liquid Water. J. Chem. Phys. 2006, 125, 184507 10.1063/1.2386157. [DOI] [PubMed] [Google Scholar]
- Riccardi D.; Li G.; Cui Q. Importance of the van der Waals Interaction in QM/MM Simulations. J. Phys. Chem. B 2004, 108, 6467–6478. 10.1021/jp037992q. [DOI] [PubMed] [Google Scholar]
- Luan B.; Huynh T.; Zhou R. Simplified TiO2 Force Fields for Studies of its Interaction with Biomolecules. J. Chem. Phys. 2015, 142, 234102 10.1063/1.4922618. [DOI] [PubMed] [Google Scholar]
- Egashira M.; Kawasumi S.; Kagawa S.; Seiyama T. Temperature Programmed Desorption Study of Water Adsorbed on Metal Oxides. I. Anatase and Rutile. Bull. Chem. Soc. Jpn. 1978, 51, 3144–3149. 10.1246/bcsj.51.3144. [DOI] [Google Scholar]
- Beck D. D.; White J. M.; Ratcliffe C. T. Catalytic Reduction of CO with Hydrogen Sulfide. 2. Adsorption of H2O and H2S on Anatase and Rutile. J. Phys. Chem. 1986, 90, 3123–3131. 10.1021/j100405a018. [DOI] [Google Scholar]
- Zhang H.; Gilbert B.; Huang F.; Banfield J. F. Water-Driven Structure Transformation in Nanoparticles at Room Temperature. Nature 2003, 424, 1025–1029. 10.1038/nature01845. [DOI] [PubMed] [Google Scholar]
- Selçuk S.; Selloni A. Surface Structure and Reactivity of Anatase TiO2 Crystals with Dominant {001} Facets. J. Phys. Chem. C 2013, 117, 6358–6362. 10.1021/jp402100v. [DOI] [Google Scholar]
- Łodziana Z.; Topsøe N.-Y.; Nørskov J. K. A Negative Surface Energy for Alumina. Nat. Mater. 2004, 3, 289–293. 10.1038/nmat1106. [DOI] [PubMed] [Google Scholar]
- Ping Y.; Sundararaman R.; Goddard W. A. III Solvation Effects on the and Edge Positions of Photocatalysts from First Principles. Phys. Chem. Chem. Phys. 2015, 17, 30499–30509. 10.1039/C5CP05740J. [DOI] [PubMed] [Google Scholar]
- Xiong G.; Shao R.; Droubay T. C.; Joly A. G.; Beck K. M.; Chambers S. A.; Hess W. P. Photoemission Electron Microscopy of TiO2 Anatase Films Embedded with Rutile Nanocrystals. Adv. Funct. Mater. 2007, 17, 2133–2138. 10.1002/adfm.200700146. [DOI] [Google Scholar]
- Spadavecchia F.; Cappelletti G.; Ardizzone S.; Ceotto M.; Falciola L. Electronic Structure of Pure and N-Doped TiO2 Nanocrystals by Electrochemical Experiments and First Principles Calculations. J. Phys. Chem. C 2011, 115, 6381–6391. 10.1021/jp2003968. [DOI] [Google Scholar]
- Agosta L.; Brandt E. G.; Lyubartsev A. P. Diffusion and Reaction Pathways of Water near Fully Hydrated TiO2 Surfaces from Ab Initio Molecular Dynamics. J. Chem. Phys. 2017, 147, 024704 10.1063/1.4991381. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.