A novel pathway analysis approach based on the unexplained disregulation of genes

Abstract

A crucial step in the understanding of any phenotype is the correct identification of the signaling pathways that are significantly impacted in that phenotype. However, most current pathway analysis methods produce both false positives as well as false negatives in certain circumstances. We hypothesized that such incorrect results are due to the fact that the existing methods fail to distinguish between the primary dis-regulation of a given gene itself and the effects of signaling coming from upstream. Furthermore, a modern whole-genome experiment performed with a next-generation technology spends a great deal of effort to measure the entire set of 30,000–100,000 transcripts in the genome. This is followed by the selection of a few hundreds differentially expressed genes, step that literally discards more than 99% of the collected data. We also hypothesized that such a drastic filtering could discard many genes that play crucial roles in the phenotype. We propose a novel topology-based pathway analysis method that identifies significantly impacted pathways using the entire set of measurements, thus allowing the full use of the data provided by NGS techniques. The results obtained on 24 real data sets involving 12 different human diseases, as well as on 8 yeast knock-out data sets show that the proposed method yields significant improvements with respect to the state-of-the-art methods: SPIA, GSEA and GSA.

Availability

Primary dis-regulation analysis is implemented in R and included in ROntoTools Bioconductor package (versions ≥ 2.0.0). https://www.bioconductor.org/packages/release/bioc/html/ROntoTools.html

I. Introduction

The goal of pathway analysis methods is to identify the most perturbed pathways in a given condition. Pathways are divided in two main categories: i) signaling pathways, that are defined as graphs in which nodes represent genes/proteins and edges are interactions between them, and ii) metabolic pathways in which the nodes represent biochemical compounds and the edges represent reactions, carried out by enzymes which are coded by genes [32]. Such pathways describe all known phenomena involved in a biological process (e.g. cell cycle), disease (e.g. Alzheimer’s disease), etc. In this paper, we focus on signaling pathways to be able to map the measured expression level of the genes to the corresponding nodes in those pathways. Intuitively, the impact of a given phenotype on a given pathway should be determined by the number of differentially expressed (DE) genes on the given pathway, the magnitude of the changes in the expression level of the genes, and the type, direction and strength of the interactions between the genes in that pathway.

The simplest pathway analysis approach is the over-representation analysis (ORA) [23]. This approach considers only the number of DE genes that are present in a given pathway. ORA techniques calculate the probability of finding a certain number of DE genes among all the genes in a pathway just by chance. Another approach to pathway analysis is the functional class scoring (FCS) [24], [32]. This approach takes into consideration all measured expression changes, as well as the correlation between the expression change of the genes and the phenotype. The most popular techniques in the FCS category are Gene Set Enrichment Analysis (GSEA) [45] and Gene Set Analysis (GSA) [10]. These two techniques rank the genes based on the correlation between their expression and a given phenotype, and calculate a score that reflects the degree to which a given pathway is represented at extremes of the ranked list. Neither of these two approaches considers the interactions between genes, their direction, type, strength, etc. In essence, all these methods treat the pathways as simple sets of genes.

However, databases such as KEGG [34], BioCarta [5] and Reactome [21] provide pathways that consist of much more than just sets of genes. These databases provide complex graphs for each signaling pathways in which each node is a gene/protein and each edge is an interaction between two such genes or proteins. Ignoring the wealth of knowledge captured in the topology of the pathway is clearly sub-optimal. Even though these databases provide more detailed information about the topology of the pathways, there are thousands of genes that have not been annotated yet. Furthermore, many of the existing annotations may be inaccurate [24]. However, we believe that accuracy and reliability of pathways annotation is growing and using this type of information can only help the interpretation of high-throughput experiments.

One of the first methods to exploit the information about the interactions among genes tried to analyze the entire set of known interactions, in order to find circuits, or subnetworks, that are affected by the phenotype in analysis. The interactions are obtained by combining different sources of information, such as pathways, interaction databases and literature [18].

More recently, more sophisticated methods that are able to fully take into consideration all the interactions between genes in signaling pathways to find which pathway is most impacted by a given phenotype have been proposed [9]. These are sometimes referred to as “topology-aware” or “third generation” pathway analysis methods [24], [32]. The method proposed in this paper belongs to this latest generation of pathway analysis methods, inasmuch it considers the topology of the pathways, as well as the changes in expression level of the genes.

However, even the most sophisticated current pathway analysis methods still produce both false positives as well as false negatives in certain circumstances. We hypothesized that such incorrect results are due to the fact that the existing methods fail to distinguish between the primary dis-regulation of a given gene itself and the effects of signals coming from upstream. We hypothesize that better results could be achieved if one distinguishes between genes that are true sources of perturbation, e.g. due to mutations, copy number variations, epigenetic changes, etc. and genes that merely respond to perturbation signals coming from upstream. Intuitively, a pathway should be more significantly impacted if it hosts more genes that are such true sources of perturbation. The method proposed here is an attempt at capturing these differences by calculating a “primary dis-regulation” for every gene and using them to compute a total pathway perturbation and subsequent significance.

Another issue related to the traditional topological data analysis approaches involves the need for a selection of differentially expressed (DE) genes. Traditionally, the pathway analysis step is performed after a set of DE genes has been selected using some thresholds on some criteria such as fold-change and/or p-values. Typically, a set of a few hundred genes are selected as DE. However, a modern whole-genome experiment performed with a next-generation technology (NGS) provides measurements for the entire set of transcripts in the genome, albeit for a non-trivial cost in computation necessary for the assembly and quantification of millions of short reads. In addition to the high computational cost, other drawbacks are related to the large amount of storage space, and the need to specialized bioinformatics expertise to set-up and run the environment necessary for the analysis. Given that this great deal of effort is spent in order to measure over 30,000 transcripts, it makes little sense to discard approximately 99% of these measurements in order to focus on 300 or so genes that are declared to be differentially expressed. Subsequently, the pathway analysis step aims to identify system-level changes based on only these 1% of the original data collected. More recently, approaches that are able to identify significantly impacted pathways based on the entire set of measurements have been proposed [54]. Henceforth, we will refer to the original approach based on DE genes as the cut-off -based approach, and to the threshold-free approach as the all genes approach. We assessed the novel method proposed here with both types of input.

In the methods section, we describe our new proposed method in details. In the discussion section, we evaluate our method using 24 data sets involving 12 conditions from different experiments comparing human diseased versus normal tissues. The results of the proposed method using the cut-off -based approach are compared with SPIA (cut-off) [48], which also uses a pre-selected list of DE genes as input. The results of the proposed method using the all genes approach are compared with GSEA [45], GSA [10] and SPIA (all genes) [54] which use entire set of genes as input. These existing methods have been selected as the reference in our comparisons because they are among the most cited and widely used methods in the literature [32]. We also evaluate our method using eight yeast knock-out data sets from different experiments comparing samples with knock-out gene versus normal samples. The comparisons show that the proposed method is able to perform better than the most widely used pathway analysis methods, in identifying the target pathways as statistically significant.

II. Methods

The measured expression change of a gene in a given phenotype can be seen as the result of influences from upstream genes superposed on the dis-regulation incurred by that particular gene itself. We will refer to this later quantity as the primary dis-regulation (pDis). The diffusion of signals between genes in regulatory networks, called “network propagation”, can be used to find the active genes and subnetworks as well as the function of the genes in different conditions [19]. Widely used methods in this field are introduced in [57] and [52]. Here, we are using a similar approach that uses propagation between genes to calculate pDis in order to find the most impacted pathways. We propose a pathway analysis method that focuses on this primary dis-regulation.

The change in the expression level of a gene i, ΔE(g_i), can be seen as a sum of the primary dis-regulation (pDis) and the secondary dis-regulation (sDis):

$$\mathrm{\Delta }E(g_i)=\mathit{pDis}(g_i)+\mathit{sDis}(g_i)$$ (1)

The secondary dis-regulation of the gene g_i is the term that is meant to capture the perturbation reaching this particular gene from upstream. This can be calculated by adding the expression change of upstream genes normalized by the number of their downstream genes:

$$\mathrm{\Delta }E(g_i)=\mathit{pDis}(g_i)+{\displaystyle \sum _{j\in U}\frac{{\beta }_{i,j}\cdot \mathrm{\Delta }E(g_j)}{N_{d,s}(g_j)}}$$ (2)

In the equation above, ΔE(g_j) is the measured fold change of the gene g_j that is somewhere directly upstream of g_i, U is the set of all such genes directly upstream of g_i, and N_ds(g_j) is the number of genes immediately downstream of g_j (see Fig. 1). The quantity β_i,j represents efficiency of the interaction between gene i and gene j. It captures a specific value if an interaction is available between two genes. We used +1 if the interaction type is activation or expression and −1 if it is inhibition or repression as default values. This is the same approach used by the impact analysis [9].

Fig. 1.

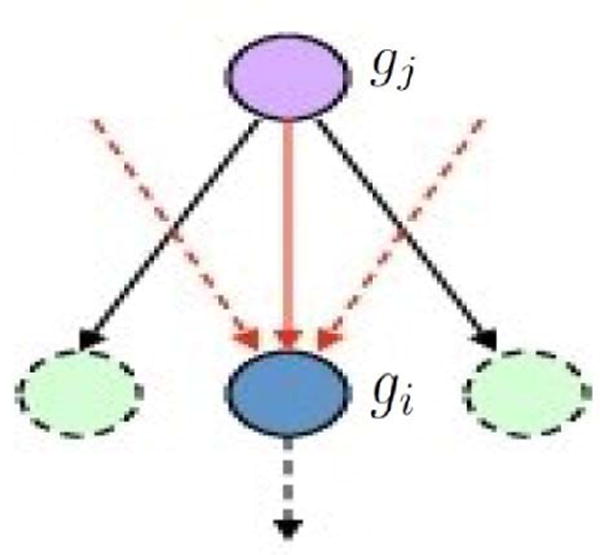
An example of one upstream gene and its three downstream genes. pDis(g_i) is calculated using its measured fold change of ΔE(g_i) and measured fold change of upstream genes (e.g. ΔE(g_j)). In this example, the number of downstream genes for g_j is N_ds(g_j) = 3.

The primary dis-regulation, which gives the change in a gene expression inherent to the gene itself, can then be derived as follows:

$$\mathit{pDis}(g_i)=\mathrm{\Delta }E(g_i)-{\displaystyle \sum _{j\in U}\frac{{\beta }_{i,j}\cdot \mathrm{\Delta }E(g_j)}{N_{ds}(g_j)}}$$ (3)

The primary dis-regulation is meant to capture information about the genes that are sources of perturbation in a given phenotype, rather than those genes that change as a result of upstream changes. For instance, a mutation that induce expression changes would be captured by the gene’s primary dis-regulation, while expression changes due to upstream signaling would be captured by the secondary dis-regulation. A mutation is an example that is sufficient but not necessary to create primary dis-regulation. Other potential cause could be copy number variations, epigenetic changes such as methylation, etc. The intuition motivating the computation of the primary dis-regulation is that pathways that have more genes that are sources of perturbation are more likely to be truly involved in the phenotype.

The process of calculating all values of the primary dis-regulation for all genes in a given pathway can be summarized using the matrix equation:

$$\mathit{pDis}=\mathrm{\Delta }{E}^T\cdot (I-B)$$ (4)

In this equation, the matrix B represents the adjacency matrix of each signaling pathway normalized by the number of downstream genes of each gene.

$$B=\left(\begin{array}{cccc}{\beta }_{1,1}/N_{ds(g_1)}& {\beta }_{1,2}/N_{ds(g_2)}& \dots & {\beta }_{1,n}/N_{ds(g_n)}\\ {\beta }_{2,1}/N_{ds(g_1)}& {\beta }_{2,2}/N_{ds(g_2)}& \dots & {\beta }_{2,n}/N_{ds(g_n)}\\ \dots & \dots & \dots & \dots \\ {\beta }_{n,1}/N_{ds(g_1)}& {\beta }_{n,2}/N_{ds(g_2)}& \dots & {\beta }_{n,n}/N_{ds(g_n)}\end{array}\right)$$

In equation 4, I is an identity matrix with dimensions equal to the number of genes in a pathway, and ΔE is the vector of measured expression changes of the genes in that pathway:

$$\mathrm{\Delta }E=\left(\begin{array}{c}\mathrm{\Delta }E(g_1)\\ \mathrm{\Delta }E(g_2)\\ \dots \\ \mathrm{\Delta }E(g_n)\end{array}\right)$$

The score for pathway k is calculated as the sum of the absolute values of primary dis-regulation of all the genes in the pathway, totalpDis:

$${\mathit{totalpDis}}_k=\sum _{{i\in \mathit{pathway}}_k}\left|\mathit{pDis}(g_i)\right|$$ (5)

The quantity totalpDis of a pathway represents the amount of primary dis-regulation of the whole pathway in the condition under study.

The significance of each pathway is assessed by computing the probability of obtaining just by chance a totalpDis value more extreme than the one observed. This probability is estimated using a bootstrap approach where the null distribution for totalpDis for each pathway is generated by sampling random gene expression changes from the original set of expression changes. The number of bootstraps used was 2,000. This process is repeated for all pathways and yields a p-value for each pathway. Subsequently, the set of p-values for all pathways are corrected for multiple comparisons using the false discovery rate (FDR). The average running time for a data set is 6.3 minutes on an architecture using a single Intel Xeon core @ 2.66GHz with 1TB of RAM.

Cut-off dependent versus cut-off free analysis

Pathway analysis techniques often take a subset of statistically significant genes as input, based on cut-offs for expression change and/or p-value. It has been shown in [35] that small variations of the threshold used to select the subset of differentially expressed (DE) genes has dramatic effects on the outcome of the methods. Hence, the accuracy of any pathway analysis methods using a subset of DE genes will also be very dependent on the threshold(s) used. Furthermore, when using a cut-off, some genes that play an important biological role may fail to meet the selection criteria and thus, not included in the set of DE genes. This can potentially impede the identification of the biologically meaningful pathways.

Recently, it has also been shown that the accuracy of a pathway analysis method can be improved by using the entire set of measurement from an experiment rather than a subset of DE genes [54]. This means that a selection of a set of DE genes may no longer be needed in many situations.

With respect to the method proposed in this paper, the use of a subset of DE genes will affect the values of the pDis of other genes in a pathway. The pDis of a gene is simply equal to the expression change when there are no upstream DE genes. However, when such upstream genes do exist, pDis is calculated using the expression changes of upstream genes as well. The inclusion of all genes in the calculation will have a strong impact on the result, even if the expression changes are small. This allows the analysis to retain all of the information in the data, avoiding arbitrary threshold choices.

We refer to this method as pDis analysis (all genes), as opposed to pDis analysis (cut-off) for cut-off based. Here, we show the results from both types of input sets applied to our new method proposed in this paper.

III. Discussion and Results

Ranks and p-values for targeted data sets

To date there is no universally accepted technique for the validation of the results of pathway analysis methods. The assessment of the results of different pathway analysis methods usually involves the selection of a few data sets, and then the interpretation of the results either with the help of biologists in the field, or by searching the published literature. This approach is very limited because it can only be applied to a small number of data sets. Furthermore, it is subjective, and may lead to bias in the results since most of the time the expert who performs the assessment is also a co-author of the paper. Finally, the biological phenomena are so complex that with enough literature search, a large number of pathways can be implicated in almost any condition. In this work we follow two validation approaches. The first one is the validation approach introduced in [47]. We like this evaluation approach because it is objective, reproducible, based on multiple data sets, and it does not require an unavoidably biased “expert” human evaluation of the results [47]. This approach requires testing on a large number (at least 10 but preferably more) of different data sets coming from a variety of different conditions, tissues, and laboratories. The data sets are selected such that there are specific pathways in the target pathway databases that model each of the given diseases. For each data set, the pathway corresponding to the phenotype is considered to be the target pathway (e.g. the colorectal cancer pathway will be the target pathway in a colorectal cancer data set). The evaluation focuses on the ability of each method to identify these true positive pathways as significant, and rank them as high as possible. In this paper we validated the proposed method using 24 data sets involving 12 different human diseases. These data sets are shown in Table I.

TABLE I.

The twenty-four data sets from the GEO database used to evaluate the pathway analysis methods compared in this paper. Each data set corresponds to a disease for which there is a target pathway in KEGG.

	GEO ID	Pubmed	Reference	Disease	Target Pathway
1	GSE1297	14769913	[6]	Alzheimer’s Disease	hsa05010
2	GSE5281	17077275	[27]	Alzheimer’s Disease	hsa05010
3	GSE5281	17077275	[27]	Alzheimer’s Disease	hsa05010
4	GSE5281	17077275	[27]	Alzheimer’s Disease	hsa05010
5	GSE20153	20926834	[61]	Parkinson’s disease	hsa05012
6	GSE20291	15965975	[60]	Parkinson’s disease	hsa05012
7	GSE8762	17724341	[40]	Huntington’s disease	hsa05016
8	GSE4107	17317818	[16]	Colorectal Cancer	hsa05210
9	GSE8671	18171984	[41]	Colorectal Cancer	hsa05210
10	GSE9348	20143136	[15]	Colorectal Cancer	hsa05210
11	GSE14762	19252501	[58]	Renal Cancer	hsa05211
12	GSE781	14641932	[26]	Renal Cancer	hsa05211
13	GSE15471	19260470	[1]	Pancreatic Cancer	hsa05212
14	GSE16515	19732725	[36]	Pancreatic Cancer	hsa05212
15	GSE19728	NA	NA	Glioma	hsa05214
16	GSE21354	NA	NA	Glioma	hsa05214
17	GSE6956	18245496	[56]	Prostate Cancer	hsa05215
18	GSE6956	18245496	[56]	Prostate Cancer	hsa05215
19	GSE3467	16365291	[13]	Thyroid Cancer	hsa05216
20	GSE3678	NA	NA	Thyroid Cancer	hsa05216
21	GSE9476	17910043	[44]	Acute myeloid leukemia	hsa05221
22	GSE18842	20878980	[42]	Non-Small Cell Lung Cancer	hsa05223
23	GSE19188	20421987	[17]	Non-Small Cell Lung Cancer	hsa05223
24	GSE3585	17045896	[3]	Dilated cardiomyopathy	hsa05414

The second approach uses knock-out data sets. In this case, the exact source of perturbation is known: the specific gene being knock-out. Thus the pathways that include this gene will be truly relevant to the phenotype, since they contain the very source of the perturbation that created the phenotype. In other words, these pathways are true positives and are also considered the target pathways in our validation.

The p-values (representing the probability of observing the given perturbations just by chance) are used to assign significance to each pathway. The list of pathways is then ranked based on these p-values.

In order to formalize and quantify the assessment, we define an “improvement factor” that will be used to compare the performance of two pathway analysis methods. If the target pathway for a given data set goes from not significant in the results of method 1 to significant in the results of method 2, the improvement factor for this data set will be 1 (see Fig. 2). If the target pathway goes from significant to not significant, the improvement factor will be −1. If the significance of the target pathway does not change but the ranking improves, the improvement factor will be +0.5. Finally, if the significance does not change but the ranking worsens, the improvement will be −0.5. If the ranking remains the same, the improvement is zero for that data set. The improvement of method 2 compared to method 1 is the average of improvement factors associated to each target pathway over the set of 24 different data sets. If the overall improvement is positive, then method 2 is considered to perform better than method 1 based on this validation method.

Fig. 2.

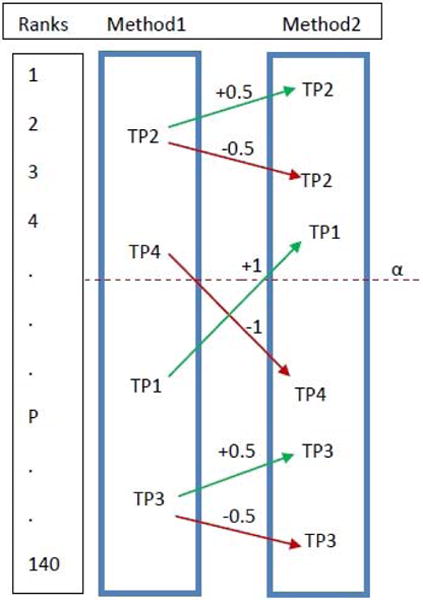
The criteria used to assess the results. Alpha (α) represents the chosen significance threshold. The green and red arrows denote situations in which method 2 is better or worse than method 1, respectively. The number on each arrow represents the value the improvement factor in each case. If a target pathway becomes significant in the results of method 2, the improvement factor for that target pathway will be +1 (e.g. target pathway TP1); if the pathway becomes not significant, the improvement factor is considered −1 (e.g. TP4). If the target remains on the same side of the significance threshold, the improvement factor is considered +0.5 or −0.5 based on the improvement or deterioration of the rank, respectively (e.g. TP2 and TP3).

The proposed method was implemented using the R statistical programming environment [50]. The code is currently available by request from the authors. We are also planning to make the code available as a Bioconductor R package. We used KEGG signaling pathways as input pathways. The pathways were obtained from the “SPIA” R package version 2.14.0 [49] as included in Bioconductor version 2.13, released on October 15th, 2013. We selected all pathways that have at least one interaction with the type of activation, inhibition, repression or expression between their genes. This resulted in a set of 139 pathways. The results of pDis analysis (all genes) are compared to GSA, GSEA and SPIA (all genes) and the results of pDis analysis (cut-off) are compared to SPIA (cut-off). SPIA (cut-off) combines two different p-values. One is the perturbation p-value (pPERT) of a pathway. The perturbation p-value is computed based on the perturbation accumulation of the pathway, which is the sum of the perturbation factors of its genes. The other p-value of SPIA is the hypergeometric p-value, based on the number of DE genes in the pathway in a given data set. Since the number of DE genes in each pathway does not depend on the analysis method, the hypergeometric p-value is the same in SPIA (cut-off) and the method proposed in this paper.

Each data set was normalized by the “mar” normalization method available in the “affy” R package (version 1.38.1) [20] from Bioconductor version 2.12, release on April 4th, 2013. For each gene, the probe id was mapped to gene Entrez ID. The fold change between normal and disease conditions for each probe was calculated by using the “limma” package (version 3.16.8) [43] from Bioconductor version 2.12, release on April 4th, 2013. We used the log2-transform of the fold changes for each gene in our analysis. The moderated t-test was performed on each probe to compute the significance of the changes between two phenotypes. For the methods that use cut-off approach, we used a 5% threshold to select the DE genes.

Ranks and p-values of target pathways for 24 disease data sets

The ranks and p-values of target pathways in all human disease data sets are shown in Fig. 3. The details of the results for the proposed and reference methods are provided in Table III (SPIA and pDis analysis (cut-off) and Table IV, V and VI (GSEA, GSA, SPIA (all genes) and pDis analysis (all genes)). The distributions of the ranks and the p-values obtained for the target pathways in four methods are shown as boxplots in Fig. 3.

Fig. 3.

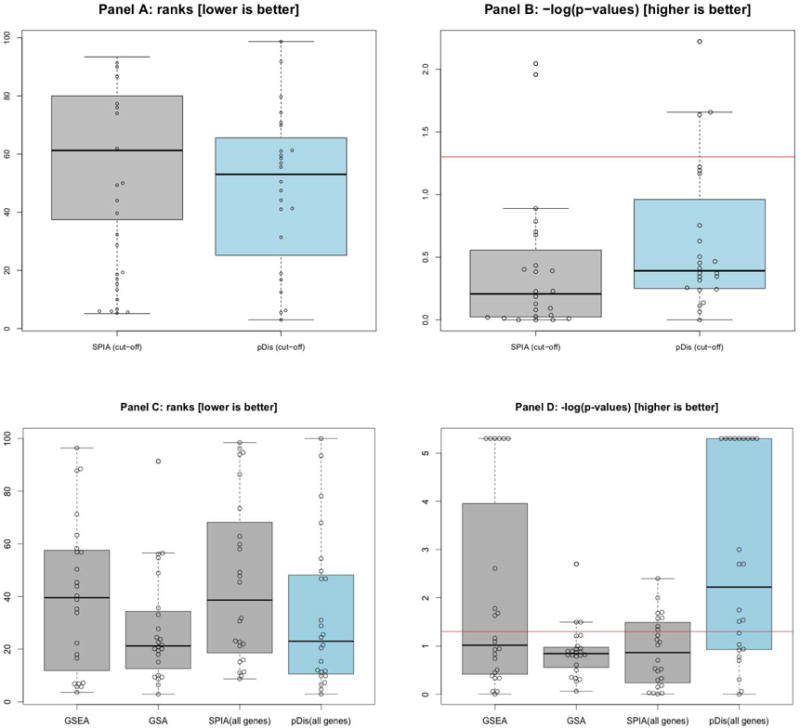
The ranks (in the left column, lower is better) and negative log of p-values of the target pathways (in the right column, higher is better) in the proposed and reference methods. The first row (panel A and panel B) shows the comparison between methods using a set of DE genes: pDis (cut-off) and SPIA (cut-off). The second row (panel C and panel D) shows the comparison between methods using all genes: GSEA, GSA and SPIA (all genes), pDis (all genes). For SPIA, the comparisons are based on the perturbation p-value (pPERT). All human signaling pathways from KEGG (139 pathways) were used in the comparisons. The data show the results obtained for the target pathways in the 24 data sets shown in Table I. The bold line in the boxplots represents the median of the distribution. These distributions show that the proposed method pDis analysis (in blue) is never significantly worse than any of the existing methods, while it yields a statistically significant improvement in 5 out of the 8 comparisons (see Table II).

TABLE III.

The ranks and the p-values of the 24 target pathways for SPIA (cut-off) and pDis analysis (cut-off). The improvement factor based on Fig. 2 is calculated for each data set considering the 5% significance threshold using FDR-corrected p-values. The average improvement factor shows that pDis analysis (cut-off) improves 12.5% compared to SPIA. As shown, the average p-value and rank for the target pathways are lower (i.e. better) in pDis analysis (cut-off) than in SPIA.

	GEO ID	Target pathway	SPIA (pPERT)			pDis analysis (cut-off)			Improvement Compared to SPIA
			p-values	FDR	ranks	p-values	FDR	ranks
1	GSE1297	Alzheimer’s Disease	0.916	1.00	78.79	0.729	0.987	70.83	+0.5
2	GSE5281	Alzheimer’s Disease	0.807	1.00	71.53	0.022	0.328	6.20	+0.5
3	GSE5281	Alzheimer’s Disease	0.956	1.00	92.54	0.006	0.201	2.99	+0.5
4	GSE5281	Alzheimer’s Disease	0.831	0.985	82.20	0.068	0.359	18.94	+0.5
5	GSE20153	Parkinson’s disease	1	1.00	62.82	1	1.00	98.72	−0.5
6	GSE20291	Parkinson’s disease	0.129	0.712	18.10	0.425	0.803	50.48	−0.5
7	GSE8762	Huntington’s disease	1	1.00	69.49	0.425	0.524	79.66	−0.5
8	GSE4107	Colorectal Cancer	0.011	0.213	5.15	0.023	0.184	12.50	−0.5
9	GSE8671	Colorectal Cancer	0.406	0.778	50.74	0.351	0.772	44.12	+0.5
10	GSE9348	Colorectal Cancer	0.198	0.503	37.96	0.387	0.679	56.93	−0.5
11	GSE14762	Renal Cancer	0.009	0.07	12.04	0.482	0.786	61.31	−0.5
12	GSE781	Renal Cancer	0.412	1.00	36.94	0.859	0.935	91.79	−0.5
13	GSE15471	Pancreatic Cancer	0.651	0.843	76.47	0.451	0.757	59.56	+0.5
14	GSE16515	Pancreatic Cancer	0.94	1.00	88.15	0.452	0.796	55.56	+0.5
15	GSE19728	Glioma	0.979	1.00	91.24	0.235	0.485	47.45	+0.5
16	GSE21354	Glioma	0.367	0.744	49.26	0.342	0.560	61.03	−0.5
17	GSE6956	Prostate Cancer	0.21	1.00	17.28	0.771	0.981	74.26	−0.5
18	GSE6956	Prostate Cancer	0.592	1.00	54.13	0.555	0.993	41.32	+0.5
19	GSE3467	Thyroid Cancer	0.745	0.957	77.78	0.57	0.925	58.52	+0.5
20	GSE3678	Thyroid Cancer	0.59	0.987	59.70	0.313	0.706	41.04	+0.5
21	GSE9476	Acute myeloid leukemia	0.164	0.841	18.11	0.064	0.825	5.51	+0.5
22	GSE18842	Non-Small Cell Lung Cancer	0.395	0.857	44.53	0.06	0.348	16.79	+0.5
23	GSE19188	Non-Small Cell Lung Cancer	0.97	1.00	93.43	0.176	0.560	31.39	+0.5
24	GSE3585	Dilated cardiomyopathy	1	1.00	81.18	0.577	0.825	69.89	+0.5
Average			0.595	0.854	57.06	0.389	0.682	48.19	+3/24=12.5%

TABLE IV.

The ranks and the p-values of the 24 target pathways for GSA and pDis analysis (all genes). The improvement factor based on Fig. 2 is calculated for each data set considering 5% significance threshold using FDR-corrected p-values. The average improvement factor shows that pDis analysis (all genes) improves the results 33.3% compared to GSA. Twelve target pathways were found to be significant in pDis analysis (all genes) while non of the target pathways have significant FDR-corrected p-values in GSA. As shown, the average p-value for the target pathways are lower (i.e. better) in the pDis analysis (all genes) than in GSA.

	GEO ID	Target pathway	GSA			pDis analysis (all genes)			Improvement Compared to GSA
			p-values	FDR	ranks	p-values	FDR	ranks
1	GSE1297	Alzheimer’s Disease	0.100	0.514	19.42	5e-06	5.7e-05	4.74	+1.0
2	GSE5281	Alzheimer’s Disease	0.316	0.872	33.09	5e-06	3.6e-05	7.29	+1.0
3	GSE5281	Alzheimer’s Disease	0.116	0.488	23.74	5e-06	2.6e-05	9.85	+1.0
4	GSE5281	Alzheimer’s Disease	0.164	0.537	27.69	5e-06	2.6e-05	9.85	+1.0
5	GSE20153	Parkinson’s disease	0.542	0.885	54.67	0.002	0.008	21.53	+1.0
6	GSE20291	Parkinson’s disease	0.246	0.629	35.61	5e-06	2.2e-05	11.67	+1.0
7	GSE8762	Huntington’s disease	0.154	0.876	15.10	5e-06	1.6e-05	15.32	+1.0
8	GSE4107	Colorectal Cancer	0.154	0.764	20.14	0.002	0.009	20.43	+1.0
9	GSE8671	Colorectal Cancer	0.002	0.069	2.87	0.116	0.248	46.71	−0.5
10	GSE9348	Colorectal Cancer	0.032	0.342	9.35	0.054	0.172	31.02	−0.5
11	GSE14762	Renal Cancer	0.132	0.600	21.58	0.029	0.062	46.71	−0.5
12	GSE781	Renal Cancer	0.492	0.865	56.47	0.998	0.998	100	−0.5
13	GSE15471	Pancreatic Cancer	0.112	0.622	17.98	0.168	0.247	67.88	−0.5
14	GSE16515	Pancreatic Cancer	0.062	0.625	8.63	0.121	0.242	49.63	−0.5
15	GSE19728	Glioma	0.136	0.548	24.46	5e-06	2.2e-05	11.31	1.0
16	GSE21354	Glioma	0.128	0.547	22.66	5e-06	2.1e-05	12.04	+1.0
17	GSE6956	Prostate Cancer	0.060	0.440	9.35	0.031	0.124	24.45	−0.5
18	GSE6956	Prostate Cancer	0.032	0.451	6.47	0.001	0.013	6.56	+1.0
19	GSE3467	Thyroid Cancer	0.152	0.687	20.14	0.018	0.061	28.83	−0.5
20	GSE3678	Thyroid Cancer	0.464	0.814	56.11	0.201	0.364	54.38	+ 0.5
21	GSE9476	Acute myeloid leukemia	0.128	0.902	10.07	5e-06	9.7e-05	2.92	+1.0
22	GSE18842	Non-Small Cell Lung Cancer	0.156	0.6992	20.86	0.496	0.635	78.10	−0.5
23	GSE19188	Non-Small Cell Lung Cancer	0.446	0.844	48.92	0.874	0.925	93.43	−0.5
24	GSE3585	Dilated cardiomyopathy	0.866	0.919	91.36	0.093	0.364	25.54	+0.5
Average			0.216	0.647	27.368	0.133	0.186	32.51	+8/24=33.3%

TABLE V.

The ranks and the p-values of the 24 target pathways for GSEA and pDis analysis (all genes). The improvement factor based on Fig. 2 is calculated for each data set considering 5% significance threshold using FDR-corrected p-values. The average improvement factor shows that pDis analysis (all genes) improves the results 37.5% compared to GSEA. Twelve target pathways were found to be significant in pDis analysis (all genes) while only 2 target pathways have significant FDR-corrected p-values in GSEA. As shown, the average p-value and rank for the target pathways are lower (i.e. better) in the pDis analysis (all genes) than in GSEA.

	GEO ID	Target pathway	GSEA			pDis analysis (all genes)			Improvement Compared to GSEA
			p-values	FDR	ranks	p-values	FDR	ranks
1	GSE1297	Alzheimer’s Disease	5e-06	4e-05	5.75	5e-06	5.7e-05	4.74	+0.5
2	GSE5281	Alzheimer’s Disease	5e-06	4e-05	3.59	5e-06	3.6e-05	7.29	−0.5
3	GSE5281	Alzheimer’s Disease	5e-06	4e-04	5.75	5e-06	2.6e-05	9.85	−0.5
4	GSE5281	Alzheimer’s Disease	5e-06	4e-05	7.19	5e-06	2.6e-05	9.85	−0.5
5	GSE20153	Parkinson’s disease	0.995	1	96.40	0.002	0.008	21.53	+1
6	GSE20291	Parkinson’s disease	5e-06	4e-05	6.83	5e-06	2.2e-05	11.67	−0.5
7	GSE8762	Huntington’s disease	5e-06	0.08	6.83	5e-06	1.6e-05	15.32	+1
8	GSE4107	Colorectal Cancer	0.081	0.171	35.25	0.002	0.009	20.43	+1
9	GSE8671	Colorectal Cancer	0.312	0.625	56.83	0.116	0.248	46.71	−0.5
10	GSE9348	Colorectal Cancer	0.118	0.283	33.81	0.054	0.172	31.02	+0.5
11	GSE14762	Renal Cancer	0.148	0.261	45.32	0.029	0.062	46.71	−0.5
12	GSE781	Renal Cancer	0.356	0.584	58.27	0.998	0.998	100	−0.5
13	GSE15471	Pancreatic Cancer	0.020	0.038	38.84	0.168	0.247	67.88	−1
14	GSE16515	Pancreatic Cancer	0.002	0.019	16.54	0.121	0.242	49.63	−1
15	GSE19728	Glioma	0.069	0.121	50.35	5e-06	2.2e-05	11.31	+1
16	GSE21354	Glioma	0.114	0.248	43.88	5e-06	2.1e-05	12.04	+1
17	GSE6956	Prostate Cancer	0.023	0.170	22.30	0.031	0.124	24.45	−0.5
18	GSE6956	Prostate Cancer	0.016	0.068	17.98	0.001	0.013	6.56	+1
19	GSE3467	Thyroid Cancer	0.463	0.682	71.22	0.018	0.061	28.83	+0.5
20	GSE3678	Thyroid Cancer	0.182	0.353	40.28	0.201	0.364	54.38	−0.5
21	GSE9476	Acute myeloid leukemia	0.4662	0.808	56.83	5e-06	9.7e-05	2.92	+1
22	GSE18842	Non-Small Cell Lung Cancer	0.414	0.727	63.30	0.496	0.635	78.10	−0.5
23	GSE19188	Non-Small Cell Lung Cancer	0.870	0.995	87.76	0.874	0.925	93.43	−0.5
24	GSE3585	Dilated cardiomyopathy	0.874	1	88.48	0.093	0.364	25.54	+0.5
Average			0.23	0.34	39.98	0.133	0.186	32.51	+2.5/24=10%

TABLE VI.

The ranks and the p-values of the 24 target pathways for SPIA (all genes) and pDis analysis (all genes). The improvement factor based on Fig. 2 is calculated for each data set considering 5% significance threshold using FDR-corrected p-values. The average improvement factor shows that pDis analysis (all genes) improves the results 43.75% compared to SPIA (all genes). Twelve target pathways were found to be significant in pDis analysis (all genes) while only one target pathways have significant FDR-corrected p-values in SPIA (all genes). As shown, the average p-value and rank for the target pathways are lower (i.e. better) in the pDis analysis (all genes) than in SPIA (all genes).

	GEO ID	Target pathway	SPIA (all genes)			pDis analysis (all genes)			Improvement Compared to SPIA (all genes)
			p-values	FDR	ranks	p-values	FDR	ranks
1	GSE1297	Alzheimer’s Disease	0.095	0.414	22.72	5e-06	5.7e-05	4.74	+1
2	GSE5281	Alzheimer’s Disease	0.661	0.880	73.48	5e-06	3.6e-05	7.29	+1
3	GSE5281	Alzheimer’s Disease	0.060	0.255	23.10	5e-06	2.6e-05	9.85	+1
4	GSE5281	Alzheimer’s Disease	0.332	0.695	47.72	5e-06	2.6e-05	9.85	+1
5	GSE20153	Parkinson’s disease	0.021	0.170	11.36	0.002	0.008	21.53	+1
6	GSE20291	Parkinson’s disease	0.020	0.174	10.98	5e-06	2.2e-05	11.67	+1
7	GSE8762	Huntington’s disease	0.955	0.992	96.21	5e-06	1.6e-05	15.32	+1
8	GSE4107	Colorectal Cancer	0.010	0.101	9.84	0.002	0.009	20.43	+1
9	GSE8671	Colorectal Cancer	0.991	1.00	98.48	0.116	0.248	46.71	+0.5
10	GSE9348	Colorectal Cancer	0.197	0.433	45.45	0.054	0.172	31.02	+0.5
11	GSE14762	Renal Cancer	0.004	0.025	15.90	0.029	0.062	46.71	−1
12	GSE781	Renal Cancer	0.074	0.338	21.21	0.998	0.998	100	−0.5
13	GSE15471	Pancreatic Cancer	0.039	0.125	30.68	0.168	0.247	67.88	−0.5
14	GSE16515	Pancreatic Cancer	0.046	0.144	31.81	0.121	0.242	49.63	−0.5
15	GSE19728	Glioma	0.301	0.502	59.84	5e-06	2.2e-05	11.31	+1
16	GSE21354	Glioma	0.026	0.118	21.96	5e-06	2.1e-05	12.04	+1
17	GSE6956	Prostate Cancer	0.083	0.543	15.15	0.031	0.124	24.45	−0.5
18	GSE6956	Prostate Cancer	0.027	0.294	8.71	0.001	0.013	6.56	+1
19	GSE3467	Thyroid Cancer	0.936	0.990	93.93	0.018	0.061	28.83	+0.5
20	GSE3678	Thyroid Cancer	0.951	0.977	94.69	0.201	0.364	54.38	+0.5
21	GSE9476	Acute myeloid leukemia	0.512	0.793	62.87	5e-06	9.7e-05	2.92	+1
22	GSE18842	Non-Small Cell Lung Cancer	0.294	0.591	49.24	0.496	0.635	78.10	−0.5
23	GSE19188	Non-Small Cell Lung Cancer	0.712	0.824	86.36	0.874	0.925	93.43	−0.5
24	GSE3585	Dilated cardiomyopathy	0.471	0.801	57.95	0.093	0.364	25.54	+0.5
Average			0.325	0.507	45.40	0.133	0.186	32.51	+11/24=43.75%

The paired t-test and the paired Wilcoxon test were performed to compare the distribution of the ranks and p-values of target pathways in each method. The results are shown in table II. The statistical tests are performed as one-tail tests in order to test whether the ranks and p-values of target pathways in proposed methods are significantly lower than the reference methods. The results show that the p-values of the target pathways in pDis analysis (cut-off) are significantly lower than SPIA. Furthermore, the ranks and the p-values of the target pathways in pDis analysis (all genes) is significantly lower than GSEA. The p-values of pDis analysis (all genes) are also lower than those yielded by GSA but not significantly so (at 5%).

TABLE II.

Results of the statistical tests that were performed to compare the results of the various methods. pDis analysis (cut-off) was compared to SPIA (cut-off). pDis analysis (all genes) was compared to GSEA, GSA and SPIA (all genes). Each p-value shows whether the ranks and the p-values of the target pathways in proposed method are significantly lower than the reference methods (at 5% significance threshold). The results show that pDis analysis (cut-off) yields significantly better p-values than SPIA (cut-off) for the target pathways. Also, pDis analysis (all genes) yields lower p-values as well as lower ranks compared to GSEA and SPIA (all genes).

P-value (paired t.test p-value)	SPIA (cut-off)	GSA	GSEA	SPIA (all genes)
pDis analysis (cut-off)	0.01	–	–	–
pDis analysis (all genes)	–	0.07	0.074	0.01

Ranks (paired Wilcoxon.test p-value)	SPIA (cut-off)	GSA	GSEA	SPIA (all genes)
pDis analysis (cut-off)	0.13	–	–	–
pDis analysis (all genes)	–	0.75	0.29	0.05

The pDis analysis (all genes) yields better results compared to GSEA, in term of both ranks (panel C in Fig. 3, Wilcoxon test p-value = 0.29), as well as p-values of the target pathways (panel D in Fig. 3, t-test p-value = 0.074). The proposed method yields significantly better results compared to SPIA (all genes) in terms of both ranks (panel C in Fig. 3, Wilcoxon test p-value = 0.05), as well as p-values of the target pathways (panel D in Fig. 3, t-test p-value =0.01). The results also show that the proposed method provides more significant p-values compared to GSA, even thought the differences are not statistically significant (see Table II). There is not significant difference between the ranks yielded by pDis (all genes) and GSA. The figure also shows the comparison between pDis analysis (cut-off) and SPIA (cut-off). The proposed method yields significantly better results compared to SPIA (cut-off) in terms of p-values (panel B in Fig. 3, t-test p=0.01). The results are also better in terms of ranks, even though the difference is not statistically significant (panel A in Fig 3, Wilcoxon test p-value =0.13).

As some diseases are complex phenotypes involving fundamental biochemical pathways, other pathways might be significantly impacted in addition to the target pathway. Therefore, we studied the detailed results of pDis analysis (all genes) on a data set, in order to show that our method is not limited to identifying the target pathway as significantly impacted, but it is also able to correctly report relevant fundamental biochemical mechanisms in the condition under study. We chose to perform detailed analysis of the first neurodegenerative disease as it appears in table I. We provide the information about the p-values of all the analyzed pathways with FDR-corrected p-value lower that 5% for the data set studying alzheimer disease [6] (see table VII). The pathways with bold font in each table indicate the pathways that are known to be related to that disease based on existing literature. We can see that most of the significant pathways are biologically meaningful in the condition in analysis, showing high precision in the results. These results indicate that the proposed method is able to report the target pathways as more significant and ranked higher, compared to the state-of-the-art methods for pathway analysis, as well as it is able to report as significant the pathways that are known to be associated to a given disease.

TABLE VII.

The resulting ranks and p-values for all the pathways from analyzing the data set that studies alzheimer disease [6] that have FDR-corrected p-value lower than 5%. We studied the association of these top pathways to alzheimer disease. The pathway shown in red is the target pathway with the name corresponding to the disease under study. The bold pathways are the ones with known association with alzheimer disease based on existing literature. The number of bold and red pathways represents the number of true positives found by the method. Here we can see 16 true positives with FDR-corrected p-value lower than 5%.

	Name	ID	p-values	FDR	ranks	references
1	Alzheimer’s disease	05010	5e-06	5e-05	4.74
2	Cytokine-cytokine receptor interaction	04060	5e-06	5e-05	4.74	[39]
3	Glutamatergic synapse	04724	5e-06	5e-05	4.74	[11]
4	GABAergic synapse	04727	5e-06	5e-05	4.74	[28]
5	Dopaminergic synapse	04728	5e-06	5e-05	4.74	[30]
6	Long-term depression	04730	5e-06	5e-05	4.74	[37]
7	Endocrine and other factor-regulated calcium reabsorption	04961	5e-06	5e-05	4.74
8	Parkinson’s disease	05012	5e-06	5e-05	4.74	[2], [8]
9	Amyotrophic lateral sclerosis (ALS)	05014	5e-06	5e-05	4.74	[31]
10	Huntington’s disease	05016	5e-06	5e-05	4.74	[12], [8]
11	Vibrio cholerae infection	05110	5e-06	5e-05	4.74
12	Pathogenic Escherichia coli infection	05130	5e-06	5e-05	4.74
13	Oocyte meiosis	04114	1e-03	0.01	10.95
14	Long-term potentiation	04720	1e-03	0.01	10.95	[51], [25]
15	Retrograde endocannabinoid signaling	04723	1e-03	0.01	10.95	[33]
16	Gastric acid secretion	04971	1e-03	0.01	10.95
17	Pancreatic secretion	04972	1e-03	0.01	10.95
18	VEGF signaling pathway	04370	2e-03	0.01	13.87	[38], [14]
19	Epithelial cell signaling in Helicobacter pylori infection	05120	2e-03	0.01	13.87
20	Systemic lupus erythematosus	05322	2e-03	0.01	13.87
21	Salmonella infection	05132	3e-03	0.02	15.33
22	Calcium signaling pathway	04020	0.01	0.03	16.79	[59], [7]
23	Salivary secretion	04970	0.01	0.03	16.79
24	Arrhythmogenic right ventricular cardiomyopathy (ARVC)	05412	0.01	0.03	16.79
25	Gap junction	04540	0.01	0.03	18.25	[29], [46]
26	Phosphatidylinositol signaling system	04070	0.01	0.04	18.98	[62], [4]
27	Morphine addiction	05032	0.01	0.04	19.71
28	Protein processing in endoplasmic reticulum	04141	0.01	0.04	20.80	[53]
29	Shigellosis	05131	0.01	0.04	20.80
30	Renal cell carcinoma	05211	0.01	0.05	21.90

Ranks and p-values for the target pathways for eight yeast knock-out data sets

We also validate our approach using eight data sets that comes from experiment studying eight yeast knock-out genes. We obtained the KEGG signaling pathways for yeast from the “ROntoTools” R package version 1.2.0 [55] as included in Bioconductor version 2.12 released on April 4th, 2013. We used all pathways that have at least one interaction of type activation, inhibition, expression, or repression. There are nine such yeast pathways in KEGG. We used the data provided by [22] as our wild type and knock-out sample. These are contained in the in the data sets GSE42215 [22] and GSE42527 [22], respectively. We selected eight knock-out data sets whose knock-out genes belong to at least one pathway considered in the analysis. The log2-fold changes for each knock-out sample were calculated by comparing expression levels of that sample with the wild type samples. Each data set was processed as described in section III. We performed the pDis analysis (all genes), SPIA (all genes) and GSA, for each of the eight knock-out sample using the calculated log2-fold changes. The target pathways for each knock-out data are the pathways that include the knock-out genes. The ranks and p-values of the target pathways for eight yeast knockout data sets are shown in the tables VIII and IX. The data show an improvement of about 50% with respect to SPIA (all genes) and an improvement of about 20% with respect to GSA. The GSEA results were not included in the comparison on the knock-out data sets because all data sets involve yeast and GSEA is not available for yeast pathways. The statistical tests are performed as one-tail in order to test whether the ranks and p-values of target pathways in proposed methods are significantly lower than the reference methods. The proposed method yields significantly better results compared to SPIA (all genes) in terms of both p-values (t-test p-value = 0.002) as well as ranks of the target pathways (Wilcoxon test p-value = 0.01). The result show that pDis (all genes) provides lower p-values (t-test p-value = 0.09) and lower ranks for the target pathways, although not significantly (Wilcoxon test p-value = 0.36) when compared to GSA.

TABLE VIII.

The ranks and the p-values of the target pathways for SPIA (all genes) and pDis analysis (all genes) using 8 yeast knock-out gene data sets. The improvement factor based on Fig. 2 is calculated for each data set considering 5% significance threshold using FDR-corrected p-values. The average improvement factor shows that pDis analysis (all genes) improves the results 50% compared to SPIA (all genes). Three target pathways were found to be significant after FDR-correction in pDis analysis (all genes) while only one target pathways have significant FDR-corrected p-values in SPIA (all genes). As shown, the average p-value and rank for the target pathways are lower (i.e. better) in the pDis analysis (all genes) than in SPIA (all genes). The results show that pDis analysis (all genes) yields significantly better p-values than SPIA (all genes) for the target pathways (p-value from t.test = 0.002) as well as it has significantly lower ranks for the target pathways compared to SPIA (all genes) (p-value from Wilcoxon test = 0.01).

	knock-out gens	target pathway	SPIA (all genes)			pDis analysis (all genes)			improvement factors compared to SPIA
			p-values	FDR	ranks	p-values	FDR	ranks
1	APC9	Cell cycle Meiosis - yeast	0.422 0.917	1 1	3 5	0.133 0.184	0.411 0.414	2 4	+0.5 +0.5
2	TPK3	Meiosis- yeast	5e-06	4.5e-05	1	5e-06	4e-05	1	–
3	RGT2	Meiosis- yeast	0.075	0.225	3	0.001	0.009	1	+1
4	USA1	Protein processing in endoplasmic reticulum	1	1	7.5	0.092	0.27	3	+0.5
5	TIF4631	RNA transport	1	1	7.5	0.084	0.756	1	–
6	URM1	Sulfur relay system	0.048	0.306	1	0.040	0.36	1	+1
7	SSM4	Protein processing in endoplasmic reticulum	1	1	7.5	0.004	0.018	2	+0.5
8	CUE1	Protein processing in endoplasmic reticulum	1	1	7.5	0.208	0.624	3	+0.5
Average			0.606	0.725	4.77	0.082	0.318	2	4.5/9=50%

TABLE IX.

The ranks and the p-values of the target pathways for GSA and pDis analysis (all genes) using 8 yeast knock-out gene data sets. The improvement factor based on Fig. 2 is calculated for each data set considering 5% significance threshold using FDR-corrected p-values. The average improvement factor shows that pDis analysis (all genes) improves the results 22.2% compared to GSA. Three target pathways were found to be significant after FDR-corrected-correction in pDis analysis (all genes) while no target pathways have significant FDR-corrected p-values in GSA. As shown, the average p-value and rank for the target pathways are lower (i.e. better) in the pDis analysis (all genes) than in GSA. The results show that pDis analysis (all genes) yields better p-values than GSA for the target pathways (p-value from t.test = 0.09) as well as it has lower ranks for the target pathways compared to GSA (p-value from Wilcoxon test = 0.36).

	knock-out gens	target pathway	GSA			pDis analysis (all genes)			improvement factors compared to GSA
			p-values	FDR	ranks	p-values	FDR	ranks
1	APC9	Cell cycle Meiosis - yeast	0.05 0.06	0.28 0.28	1 2	0.133 0.184	0.411 0.414	2 4	−0.5 −0.5
2	TPK3	Meiosis- yeast	0.40	0.63	5	5e-06	4e-05	1	+1
3	RGT2	Meiosis- yeast	0.98	0.98	9	0.001	0.009	1	+1
4	USA1	Protein processing in endoplasmic reticulum	0.09	0.78	1	0.092	0.27	3	−0.5
5	TIF4631	RNA transport	0.78	0.88	6	0.084	0.756	1	+0.5
6	URM1	Sulfur relay system	0.02	0.09	2	0.040	0.36	1	+0.5
7	SSM4	Protein processing in endoplasmic reticulum	0.04	0.43	1	0.004	0.018	2	+1
8	CUE1	Protein processing in endoplasmic reticulum	0.04	0.31	1	0.208	0.624	3	−0.5
Average			0.27	0.51	3.1	0.082	0.318	2	2/9=22.2%

False positives under the null hypothesis

As we have demonstrated, the proposed method produces significantly lower p-values for the target pathways compared with the existing methods, across the set of 24 data sets used in the validation. However, lower p-values for the target pathways could be produced if the new method indiscriminately lowered the p-values for all pathways, thus introducing many false positives.

In order to show that this is not the case, we ran a number of experiments with completely random data. In each of these experiments, a set of expression changes are assigned to the genes from a random normal distribution with mean of zero and standard deviation of 1. This was repeated 1,000 times and p-values for the pathways were computed in each iteration. The pathway p-values for these random data sets, produced the distribution for the p-values under the null hypothesis. Null-hypothesis distributions were also calculated for each target pathway and showed no abnormal tendencies. The distribution of the pooled p-values for all pathways over the 1,000 iterations is shown in Fig. 4. Both the distribution of the pooled p-values, as well as all null distributions associated with each individual target pathway were uniform, demonstrating that our method does not yield more significant p-values for the target pathways by lowering all p-values. These distributions demonstrate that the proposed method does not produce any more false positives than appropriate for any significance threshold.

Fig. 4.

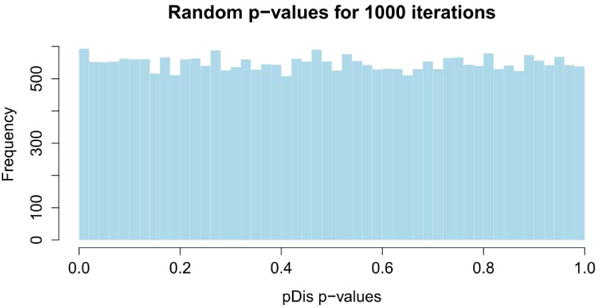
The null distribution of the p-values obtained from pDis analysis for all KEGG signaling pathway (139 pathways) in 1,000 iterations. The input gene expression values were chosen from a random normal distribution with mean of 0 and standard deviation of 1. The histogram shows the null distribution of the pooled p-values. Uniform distributions were also obtained for each individual target pathway (data not shown). The uniform distributions prove that pDis analysis does not produce any more false positives than expected.

IV. Conclusion

Here we proposed a new topological pathway analysis method based on the amount of perturbation associated with each individual gene. The proposed pDis analysis considers the dis-regulation of each gene in every pathway to calculate a p-value with respect to the distribution of the dis-regulation under the null hypothesis. The proposed method is able to use either i) a pre-selected number of DE genes, pDis analysis (cut-off), or ii) the entire list of measured expression levels, pDis analysis (all genes). The results showed that the proposed method yields significant improvements with respect to the state-of-the-art methods: SPIA, GSEA and GSA. The comparisons have been performed with a validation method that used 24 different data sets involving 12 different human diseases and eight different data sets involving eight knocked out genes in yeast.

Biographies

Sahar Ansari is a Ph.D. candidate in the department of Computer Science, Wayne State University, Detroit, MI, USA. She received his B.Sc. in Electrical Engineering in 2010 from Sharif University of Technology, Tehran, Iran. Her research interests include systems biology, data mining and biostatistics.

Calin Voichita earned his Ph.D. in computer science from Wayne State University, Detroit, MI, USA. His research efforts are focused on ways to detect abnormalities in the behavior of biological networks. He designed and implemented methods to propagate measured expression changes through gene signaling pathways without the need to select differentially express genes. He is the author of the ROntoTools package available as part of Bioconductor that make these methods available in the R language. These methods allow life scientists to take advantage of the wealth of information available with the recent RNAseq technologies. Furthermore, he applies his computational intelligence experience to develop methods that are able to identify patients that will not respond to general treatments and may require personalized solutions.

Michele Donato received his master’s degree in computer engineering from Universit di Pisa in 2006 (Italy). He received a second master’e degree in computer science from the department of computer science at Wayne State University in 2015 (USA). He also successfully defended his Ph.D. thesis to the department of computer science at Wayne State University in 2015. Currently he is a postdoctoral research fellow at Stanford University (USA).

Rebecca Tagett has a Bachelors in Physics, a Masters in Molecular Biology, and 10 years R&D experience in industry as a Computational Biologist. A PhD Candidate and a member of the Intelligent Systems and Bioinformatics Laboratory (ISBL) in the Department of Computer Science at Wayne State University, her research focuses on phenotypic prediction using multi-omics. Her interests are Functional Genomics, Scientific Writing, Bioinformatics and Biostatistics. She is a member of the International Society for Computational Biology (ISCB).

Sorin Draghici earned a Ph.D. in computer science from the University of St. Andrews, United Kingdom. He holds the Robert J. Sokol MD Endowed Chair in Systems Biology in the Department of Obstetrics and Gynecology, and is a professor in the Department of Clinical and Translational Science and the Department of Computer Science, as well as the head of the Intelligent Systems and Bioinformatics Laboratory at Wayne State University. He is also the chief of the Bioinformatics and Data Analysis Section in the Perinatology Research Branch of the National Institute for Child Health and Development. A senior member of IEEE, Dr. Draghici is an editor of IEEE/ACM Transactions on Computational Biology and Bioinformatics, Journal of Biomedicine and Biotechnology, and International Journal of Functional Informatics and Personalized Medicine. He has published two books on microarray analysis entitled Data Analysis Tools for Microarrays (Chapman and Hall/CRC Press, 2003) and Statistics and Data Analysis for Microarrays Using R and Bioconductor, Second Edition (Chapman & Hall/CRC Mathematical & Computational Biology, 2011), eight book chapters and more than 100 peer-reviewed journal and conference papers.