Fig. 2.

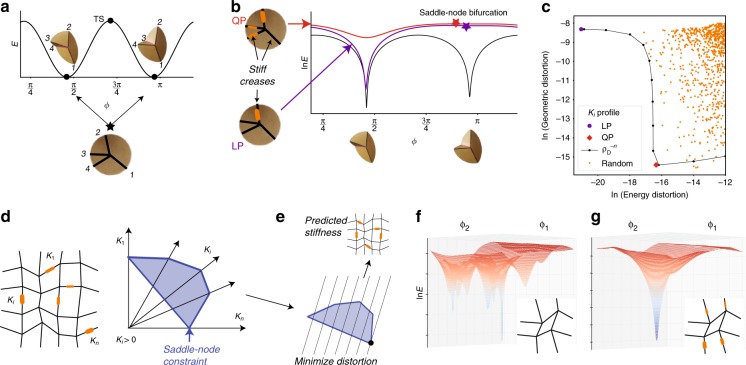
Heterogeneous stiff creases can simplify the landscape of self-folding sheets near the flat state. a An origami 4-vertex has a choice between two distinct folding modes at the flat state (ϕ—null space angle variable, see Supplementary Note 2). b Stiff creases completely eliminates a chosen mode by combining it with a nearby transition state (TS) in a saddle-node bifurcation (thickness of orange strip indicates stiffness.) c Trade-off: stiff creases distort the desired mode while eliminating undesired modes. Stiffness profiles that minimize energy distortion (e.g., the linear programming (LP) method) cause large geometric distortion and vice versa (e.g., the quadratic programming (QP) method). d The exponentially many misfolding modes of large sheets are all eliminated if the stiffness profile κ_i satisfies a linear constraint, shown here as a simplex. e We can minimize distortion (energy or geometry) of the desired mode by optimizing crease stiffness on this simplex. f, g All but one chosen minimum in a pattern’s energy landscape (at small overall folding) can be eliminated by stiff creases predicted by the procedure in (e)