Figure - PMC

Skip to main content

An official website of the United States government

Here's how you know

Here's how you know

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS
A lock ( ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

View full-text article in PMC

. 2018 Oct 25;8:15819. doi: 10.1038/s41598-018-33961-3

Search in PMC
Search in PubMed
View in NLM Catalog
Add to search

© The Author(s) 2018

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

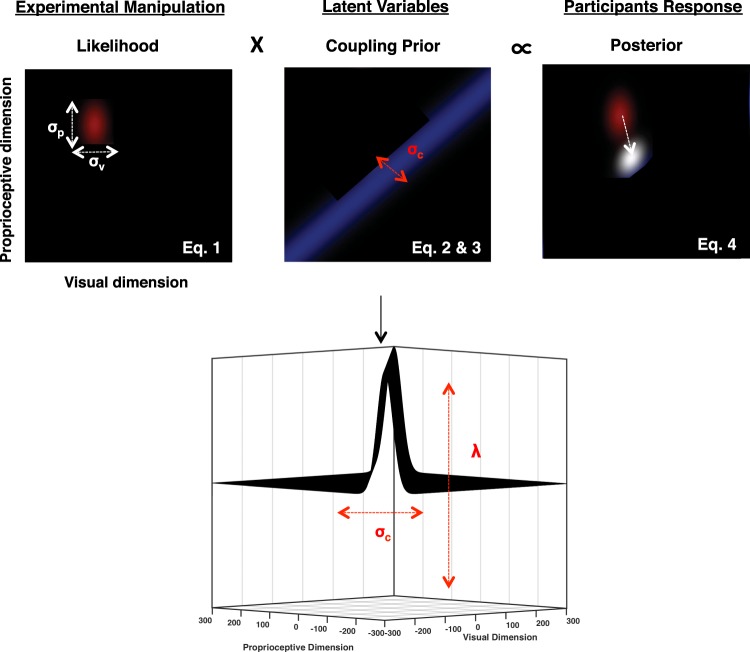
PMC Copyright notice

Coupling Prior Analyses. The experimental manipulation places visuo-proprioceptive targets within a two-dimensional space, which are represented by a bivariate Gaussian likelihoods with σ_p and σ_p that are calculated from individual reaches to proprioceptive and visual targets respectively (top leftmost panel). Within the coupling prior framework, this likelihood is multiplied with a prior for visuo-proprioceptive joint localization (middle panel) in order to yield the final posterior, from which a decision is decoded via maximum-a-posteriori (MAP; top rightmost panel). As illustrated in the bottom panel, the coupling prior is governed by two parameters, the spatial dispersion of the two-dimensional Gaussian describing the expected spatial relation between visual and proprioceptive targets (σ²_c) and the strength of this coupling (λ), which dictates the relation between integration (larger λ), and segregation (smaller λ).