Logistic regression with a continuous exposure measured in pools and subject to errors

Abstract

In a multivariable logistic regression setting where measuring a continuous exposure requires an expensive assay, a design in which the biomarker is measured in pooled samples from multiple subjects can be very cost effective. A logistic regression model for poolwise data is available, but validity requires that the assay yields the precise mean exposure for members of each pool. To account for errors, we assume the assay returns the true mean exposure plus a measurement error (ME) and/or a processing error (PE). We pursue likelihood-based inference for a binary health-related outcome modeled by logistic regression coupled with a normal linear model relating individual-level exposure to covariates and assuming that the ME and PE components are independent and normally distributed regardless of pool size. We compare this approach with a discriminant function-based alternative, and we demonstrate the potential value of incorporating replicates into the study design. Applied to a reproductive health dataset with pools of size 2 along with individual samples and replicates, the model fit with both ME and PE had a lower AIC than a model accounting for ME only. Relative to ignoring errors, this model suggested a somewhat higher (though still nonsignificant) adjusted log-odds ratio associating the cytokine MCP-1 with risk of spontaneous abortion. Simulations modeled after these data confirm validity of the methods, demonstrate how ME and particularly PE can reduce the efficiency advantage of a pooling design, and highlight the value of replicates in improving stability when both errors are present.

1 |. INTRODUCTION

A pooling study design is one in which a biomarker of interest is measured in combined biospecimen samples from multiple participants rather than individual samples.^1,2 Pooling designs may be best known for their use in ascertaining individual-level disease status with fewer assays, eg, in screening donated blood for hepatitis B virus.³ Our focus, however, is on the use of pooling for measuring a continuous biomarker and estimating parameters in an individual-level regression model of interest.

There are numerous reasons one might consider a pooling study design. For example, the assay may require a sample volume greater than is available for individual participants, or it may be too expensive to obtain individual-level measurements for every participant.⁴ In a regression setting, if pools are comprised of samples from participants who are similar on relevant characteristics, a pooling design requiring far fewer assays may offer only slightly less power than a corresponding individual-level design.^5,6 For a fixed budget, a pooling design requiring the same or fewer total assays may have much greater power than a traditional design; for a fixed target power, a pooling design may be drastically cheaper.

Logistic regression is a context in which pooling can be highly cost effective, provided that pools can be formed so that the subjects comprising them are homogeneous with respect to the outcome. Assuming the assay returns the arithmetic mean biomarker level for members of each pool, Weinberg and Umbach^4,7 provide a poolwise logistic regression model for estimating log-odds ratios for the exposure and other covariates. As they note, however, fitting this model without accounting for errors in the biomarker measurements can lead to a well-known consequence of covariate measurement error: inconsistent parameter estimation.^8,9

Schisterman et al10 describe two types of errors in particular that can affect poolwise biomarker measurements and induce bias if ignored. These are measurement error (ME), which is due to the assay being imperfect, and processing or “pooling” error (PE), which is variability induced as a result of the process of combining samples. The latter can be due to imperfect lab conditions or cross-reactions between components of blood from different participants.⁴ Schisterman et al aimed to estimate parameters of a biomarker distribution based on data from a “hybrid” design with measurements for individuals and pools of several different sizes, accounting for ME and PE by leveraging information about variance components from the different data types.

Lyles et al11 took a similar approach to account for ME and PE in estimating the covariate-adjusted log-odds ratio relating a continuous exposure measured in pools and a binary outcome. They developed a discriminant function approach that leads to a convenient poolwise model into which additive normal ME and PE can be incorporated, resulting in a closed-form likelihood for the pooled data. This approach is computationally simple and does not require homogeneous pools with respect to case status but does not produce log-odds ratio estimates for covariates other than the pooled exposure variable. The likelihood methods of Liu et al¹² are similar in that they model the pooled biomarker as the dependent variable, but their focus is solely on outcome ME as opposed to correcting an adjusted odds ratio estimate for exposure ME and/or PE.

In this paper, we follow the framework of Schisterman et al and Lyles et al to extend the Weinberg and Umbach logistic regression model to accommodate errors in the poolwise exposure. We consider a hybrid study design that includes several different pool sizes, typically including some pools of size 1 (“singles” or “single-specimen pools”). We use a maximum likelihood (ML) approach assuming processing and measurement errors are independent and normally distributed with 0 means and variances ${\sigma }_p^2$, and ${\sigma }_m^2$ that do not depend on pool size. As in Schisterman et al,¹⁰ we assume processing errors affect multispecimen pools only, while measurement errors affect single- and multi-specimen pools and have the same variance regardless of pool size.

While all parameters are identifiable with a design that includes at least three different pool sizes including 1, we demonstrate that numerical stability and precision can be improved by incorporating a relatively small number of replicates into the study design. We apply our methods to exploring the relationship between levels of a serum cytokine during pregnancy and risk of spontaneous abortion using a dataset in which cytokines were measured in pools of size 1 and 2 and in which replicate measurements are available. The discriminant function approach,¹¹ modified slightly to accommodate replicates, is included as a reference method throughout; accessible software for implementing both methods is provided.

2 |. STATISTICAL METHODS

2.1 |. Poolwise logistic regression

Suppose we wish to estimate parameters in an individual-level logistic regression model relating a binary outcome Y_ij to a continuous exposure X_ij and covariates C_ij

$$\text{logit\hspace{0.17em}}\left[P\left(Y_{ij}=1\right)\right]={\beta }_0+{\beta }_x{X}_{ij}+{\beta }_c^T{C}_{ij}.$$ (1)

Here, i indexes the eventual pool number (i = 1, …, k), and j indexes membership within a pool (j = 1, … , g_i) so that Y_ij is the case status for the jth member of the ith pool comprised of g_i members (g_i ∈ 1, 2, … ). We consider a design in which the ith pool is comprised of specimens that are homogeneous on the outcome (ie, Y_i = 1or Y_i = 0), which requires observing individual outcomes prior to forming pools in which to measure the exposure.

Rather than observing the exposure for each member of a pool, $X_i={\left(X_{i1},\dots ,X_{i{g}_i}\right)}^T$, one ideally obtains from an assay the poolwise mean ${\overline{X}}_i=\frac{1}{g_i}{\displaystyle {\sum }_{j=1}^{g_i}{X}_{ij}}$, from which the poolwise sum can be calculated as $X_i^{\ast }=g_i{\overline{X}}_i$ (asterisks denote poolwise sums throughout). While individual-level data is assumed present for the other covariates, $C_i={\left(C_{i1},\dots ,C_{i{g}_i}\right)}^T$, we similarly calculate poolwise sums $C_i^{\ast }={\displaystyle {\sum }_{j=1}^{g_i}{C}_{ij}}$.

In the absence of ME and PE in a case-control setting, Weinberg and Umbach^4,7 provide the appropriate poolwise logistic regression model for estimating $\beta ={\left({\beta }_0,{\beta }_x,{\beta }_c^T\right)}^T$

$$\text{logit\hspace{0.17em}}\left[P\left(Y_i=1\right)\right]=q_i+g_i{\beta }_0+{\beta }_x{X}_i^{\ast }+{\beta }_c^T{C}_i^{\ast }.$$ (2)

The offset is defined as

$$q_i=g_i\text{\hspace{0.17em}ln\hspace{0.17em}}\left(\frac{P\left(A|D\right)}{P\left(A|\overline{D}\right)}\right)+g_i\text{\hspace{0.17em}ln\hspace{0.17em}}\left(\frac{n_{\overline{D}}}{n_D}\right)+\text{\hspace{0.17em}ln\hspace{0.17em}}\left(\frac{\#\text{\hspace{0.17em}case\hspace{0.17em}pools of size\hspace{0.17em}}{g}_i}{\#\text{\hspace{0.17em}control\hspace{0.17em}pools\hspace{0.17em}of\hspace{0.17em}size\hspace{0.17em}}{g}_i},\right)$$ (3)

where P(A|D) and $P\left(A|\overline{D}\right)$ are accrual probabilities for cases and controls and n_D and $n_{\overline{D}}$ are the total number of cases and controls across all pools. If accrual probabilities are unknown, the first term on the right hand side can be omitted, with the only consequence being invalid estimation of β₀ if there is case oversampling.

2.2 |. ML for handling errors in $X_i^{\ast }$

As assumed in Schisterman et al,¹⁰ suppose the measurement obtained from the assay is not the precise poolwise mean ${\overline{X}}_i$ but rather the poolwise mean plus a processing error ${ϵ}_i^p$ (if g_i > 1) and a measurement error ${ϵ}_i^m$. Letting ${\tilde{\overline{X}}}_i$ represent the error-prone measurement, we assume

$${\tilde{\overline{X}}}_i={\overline{X}}_i+{ϵ}_i^{p}I\left(g_i>1\right)+{ϵ}_i^m.$$ (4)

The poolwise logistic regression model in (2) uses the poolwise sum rather than the poolwise mean, which can be calculated as ${\tilde{X}}_i^{\ast }=g_i{\tilde{\overline{X}}}_i$.

In the ith pool, we observe $\left(Y_i,{\tilde{X}}_i^{\ast },C_i^{\ast }\right)$ Conditioning on precisely measured summed covariate values $C_i^{\ast }$, the likelihood contribution is $L_i\left(\theta \right)=f\left(Y_i,{\tilde{X}}_i^{\ast }|C_i^{\ast }\right)={\displaystyle {\int }_{X_i^{\ast }}f\left(Y_i,{\tilde{X}}_i^{\ast },X_i^{\ast }|C_i^{\ast }\right)}d{X}_i^{\ast }$. Taking a classical measurement error modeling approach,⁸ we factor the likelihood as follows:

$$\begin{gathered} L_i\left(\theta \right)={\displaystyle {\int }_{X_i^{\ast }}f\left(Y_i|{\tilde{X}}_i^{\ast },X_i^{\ast },C_i^{\ast }\right)}f\left({\tilde{X}}_i^{\ast }|X_i^{\ast },C_i^{\ast }\right)f\left(X_i^{\ast }|C_i^{\ast }\right)d{X}_i^{\ast } \\ ={\displaystyle {\int }_{X_i^{\ast }}f\left(Y_i|X_i^{\ast },C_i^{\ast }\right)}f\left({\tilde{X}}_i^{\ast }|X_i^{\ast }\right)f\left(X_i^{\ast }|C_i^{\ast }\right)d{X}_i^{\ast }. \end{gathered}$$ (5)

The simplification $f\left(Y_i|{\tilde{X}}_i^{\ast },X_i^{\ast },C_i^{\ast }\right)=f\left(Y_i|X_i^{\ast }|C_i^{\ast }\right)$ reflects a standard nondifferential error assumption⁸: the imprecise ${\tilde{X}}_i^{\ast }$ does not inform the outcome given the precise $X_i^{\ast }$ and covariates. The result $f\left({\tilde{X}}_i^{\ast }|X_i^{\ast },C_i^{\ast }\right)=f\left({\tilde{X}}_i^{\ast }|X_i^{\ast }\right)$ reflects an assumption that the errors in (4) are independent of covariate values.

The three-density factorization in (5) is common in the measurement error literature, and the three components are often termed the disease model (or outcome model), the measurement error model, and the exposure model, respectively.¹³ The disease model is already determined by (2). For the measurement error model, if we assume ${ϵ}_i^p~N\left(0,{\sigma }_p^2\right)$ and ${ϵ}_i^m~N\left(0,{\sigma }_m^2\right)$ and these errors are independent, then by (4), we have ${\tilde{X}}_i^{\ast }=g_i{\tilde{\overline{X}}}_i=X_i^{\ast }+g_i{ϵ}_i^{p}I\left(g_i>1\right)+g_i{ϵ}_i^m$, leading to

$${\tilde{X}}_i^{\ast }|X_i^{\ast }~N\left(X_i^{\ast },g_i^2{\sigma }_p^{2}I\left(g_i>1\right)+g_i^2{\sigma }_m^2\right)$$ (6)

For the exposure model $X_i^{\ast }|C_i^{\ast }$, we first specify an individual-level model for X_ij | C_ij and then derive the corresponding poolwise model. A common approach in the measurement error literature and one that leads to a simple poolwise model is a normal linear regression.⁸ If we assume $X_{ij}+{\alpha }_0+{\alpha }_c^T{C}_{ij}+{ϵ}_{ij}^x,{ϵ}_{ij}^x\stackrel{\text{iid}}{~}N\left(0,{\sigma }_x^2\right)$, then $X_i^{\ast }={\displaystyle {\sum }_{j=1}^{g_i}{X}_{ij}}=g_i{\alpha }_0+{\alpha }_c^T{C}_i^{\ast }+{ϵ}_i^{x\ast },{ϵ}_i^{x\ast }\stackrel{\text{ind}}{~}N\left(0,g_i{\sigma }_x^2\right)$. Assuming ${ϵ}_i^{x\ast }$ is independent of ${ϵ}_i^p$ and ${ϵ}_i^m$, the third term in the likelihood is

$$X_i^{\ast }|C_i^{\ast }~N\left(g_i{\alpha }_0+{\alpha }_c^T{C}_i^{\ast },g_i{\sigma }_x^2\right).$$ (7)

With the likelihood contribution for each pool specified, optimization routines can be used to obtain ML estimates for $\theta ={\left({\beta }^T,{\alpha }^T,{\sigma }_x^2,{\sigma }_p^2,{\sigma }_m^2\right)}^T$, with their variance-covariance matrix obtained by numerically approximating the Hessian at the MLEs and taking its inverse. Both steps require numerically integrating out $X_i^{\ast }$ for each pool at each iteration.

2.3 |. Approximate ML

To facilitate an alternative approach designed to avoid numerical integration in (5), we first factor the density $f\left(Y_i,{\tilde{X}}_i^{\ast }|C_i^{\ast }\right)$ slightly differently to obtain the following equivalent expression for L_i(θ):

$$L_i\left(\theta \right)=\left[{\displaystyle {\int }_{X_i^{\ast }}f\left(Y_i|X_i^{\ast },C_i^{\ast }\right)}f\left(X_i^{\ast }|{\tilde{X}}_i^{\ast },C_i^{\ast }\right)\text{d}{X}_i^{\ast }\right]f\left({\tilde{X}}_i^{\ast }|C_i^{\ast }\right).$$ (8)

The first density is specified by (2). To obtain the second and third, we first derive the joint density $f\left(X_i^{\ast },{\tilde{X}}_i^{\ast }|C_i^{\ast }\right)$. Implicitly conditioning on $C_i^{\ast }$ and using the poolwise linear regression in (7) for $X_i^{\ast }|C_i^{\ast }$, we can write

$$\begin{array}{llllll}\left[\begin{array}{c}{X}_i^{\ast }\\ {\tilde{X}}_i^{\ast }\end{array}\right]\hfill & =\hfill & \left[\begin{array}{ccc}{g}_i{\alpha }_0& +& {\alpha }_c^T{C}_i^{\ast }\\ g_i{\alpha }_0& +& {\alpha }_c^T{C}_i^{\ast }\end{array}\right]\hfill & +\hfill & \left[\begin{array}{ccc}1& 0& 0\\ 1& g_{i}I\left(g_i>1\right)& g_i\end{array}\right]\hfill & \left[\begin{array}{c}{ϵ}_i^{x\ast }\\ {ϵ}_i^p\\ {ϵ}_i^m\end{array}\right]\hfill \end{array}.$$ (9)

Given the prior normality and independence assumptions, the error vector ${ϵ}_i={\left({ϵ}_i^{x\ast },{ϵ}_i^p,{ϵ}_i^m\right)}^T$ is trivariate normal, and therefore, ${\left(X_i^{\ast }|{\tilde{X}}_i^{\ast }\right)}^T$ is also normal

$$\begin{array}{cccc}\left[\begin{array}{c}{X}_i^{\ast }\\ {\tilde{X}}_i^{\ast }\end{array}\right]& ~& N_2& \left(\begin{array}{ccc}\left[\begin{array}{ccc}{g}_i{\alpha }_0& +& {\alpha }_c^T{C}_i^{\ast }\\ g_i{\alpha }_0& +& {\alpha }_c^T{C}_i^{\ast }\end{array}\right]& ,& \left[\begin{array}{cc}{g}_i{\sigma }_x^2& g_i{\sigma }_x^2\\ g_i{\sigma }_x^2& g_i{\sigma }_x^2+g_x^{2}I\left(g_i>1\right){\sigma }_p^2+g_i^2{\sigma }_m^2\end{array}\right]\end{array}\right).\end{array}$$ (10)

Hence, ${\tilde{X}}_i^{\ast }|C_i^{\ast }~N\left(g_i{\alpha }_0+{\alpha }_c^T{C}_i^{\ast },g_i{\sigma }_x^2+g_i^{2}I\left(g_i>1\right){\sigma }_p^2+g_i^2{\sigma }_m^2\right)$ and $X_i^{\ast }|\left({\tilde{X}}_i^{\ast },C_i^{\ast }\right)~N\left({\overline{\mu }}_i={\mu }_{i1}+\frac{{\sum }_{i12}}{{\sum }_{i22}}\left({\tilde{X}}_i^{\ast }-{\mu }_{i2}\right),{\overline{\sigma }}_p^2={\sum }_{i11}-\frac{{\sum }_{i12}^2}{{\sum }_{i22}}\right)$ with (μ_i1, μ_i2, Σ_i12, Σ_i22) apparent from (10).

With $Y_i|\left(X_i^{\ast },C_i^{\ast }\right)~\text{\hspace{0.17em}Bernoulli}\left(p_i={\left(1+e^{-q_i-g_i{\beta }_0-{\beta }_x{X}_i^{\ast }-{\beta }_c^T{C}_i^{\ast }}\right)}^{-1}\right)$ and $X_i^{\ast }|\left({\tilde{X}}_i^{\ast },C_i^{\ast }\right)~N\left({\overline{\mu }}_i,{\overline{\sigma }}_i^2\right)$, the integral in (8) is a variant on a logistic-normal integral that arises in logistic regression with covariate measurement error outside of the pooling context. A closed-form approximation can be used to avoid integrating out $X_i^{\ast }$ numerically.^8,14 The first density under the integral in (8) is $p_i^{y_i}{\left(1-p_i\right)}^{1-y_i}$, where $p_i=H\left({\eta }_i\right)=\frac{e^{{\eta }_i}}{1+e^{{\eta }_i}}$ and ${\eta }_i=q_i+g_i{\beta }_0+{\beta }_x{X}_i^{\ast }+{\beta }_c^T{C}_i^{\ast }$. Replacing the logistic function H(η_i) with the probit approximation $\Phi \left(\frac{{\eta }_i}{k}\right)$, where Φ(·) is the standard normal CDF and typically k = 1.7,¹⁵ leads to

$$p_i^{\ast }=P\left(Y_i=1|{\tilde{X}}_i^{\ast },C_i^{\ast }\right)\approx H\left(\frac{q_i+g_i{\beta }_0+{\beta }_x{\overline{\mu }}_i+{\beta }_c^T{C}_i^{\ast }}{\sqrt{1+\frac{{\beta }_x^2{\overline{\sigma }}_i^2}{{1.7}^2}}}\right).$$ (11)

Thus, the integral in (8), which represents $f\left(Y_i|{\tilde{X}}_i^{\ast },C_i^{\ast }\right)$, can be approximated by the closed-form expression $p_i^{*y_i}{\left(1-p_i^{\ast }\right)}^{1-y_i}$. Thoresen and Laake note that the probit approximation should perform well for disease probabilities between 0.1 and 0.9.¹⁶ Approximate ML estimates and standard errors can be obtained using the same procedures as for full ML, but without numerical integration.

As noted by a reviewer, (11) has been used in the pooling context before. Zhang and Albert¹⁷ encountered a logistic-normal integral in developing regression calibration models to account for individual-level biomarker levels differing from observed poolwise means. Their scenario is different in that pools are not homogeneous with respect to case status, and measurement and processing errors are not considered.

2.4 |. Discriminant function approach

An alternative to poolwise logistic regression is the discriminant function approach described by Lyles et al.¹¹ The basic idea is to estimate β_x, the same exposure-disease log-odds ratio in (1), using estimated parameters from a normal-errors linear regression of X_ij on (Y_ij, C_ij) rather than a logistic regression of Y_ij on (X_ij, C_ij). The assumed model is

$$X_{ij}={\gamma }_0+{\gamma }_y{Y}_{ij}+{\gamma }_c^T{C}_{ij}+{ϵ}_{ij},{ϵ}_{ij}\stackrel{\text{iid}}{~}N\left(0,{\sigma }^2\right).$$ (12)

If this assumption holds, it can be shown that the quantity $\frac{{\gamma }_y}{{\sigma }^2}$ represents the same adjusted log-odds ratio targeted by β_x in (1).¹⁸ While the ML estimate for the log-odds ratio is ${\widehat{log-\text{OR}}}_{ml}=\frac{{\widehat{\gamma }}_y}{{\widehat{\sigma }}^2}$, one can also use a bias-adjusted version of the estimator resulting from a second-order Taylor series expansion¹¹

$${\widehat{\log -\text{OR}}}_{adj}={\widehat{\log -\text{OR}}}_{ml}-\frac{{\widehat{\gamma }}_y\widehat{V}\left({\widehat{\sigma }}^2\right)}{{\left({\widehat{\sigma }}^2\right)}^3}.$$ (13)

Given the individual-level linear regression in (12), the poolwise model for the sum is

$$X_i^{\ast }={\displaystyle {\sum }_{j=1}^{g_i}{X}_{ij}}=g_i{\gamma }_0+{\gamma }_y{Y}_i^{\ast }+{\gamma }_c^T{C}_i^{\ast }+{ϵ}_i^{\ast },{ϵ}_i^{\ast }\stackrel{\text{ind}}{~}N\left(0,g_i{\sigma }^2\right).$$ (14)

Here, $Y_i^{\ast }$ is the number of subjects with Y_ij = 1 in the ith pool, as opposed to the logistic regression setup where Y_i = 1 for case pools and 0 for control pools. We again assume the assay returns the error-contaminated poolwise mean ${\tilde{\overline{X}}}_i={\overline{X}}_i+{ϵ}_i^{p}I\left(g_i>1\right)+{ϵ}_i^m$, from which we calculate the poolwise sum ${\tilde{X}}_i^{\ast }=g_i{\tilde{\overline{X}}}_i=X_i^{\ast }+g_i{ϵ}_i^{p}I\left(g_i>1\right)+g_i{ϵ}_i^m$. The likelihood contribution for the observed $\left(Y_i^{\ast },{\tilde{X}}_i^{\ast },C_i^{\ast }\right)$ is $L_i\left(\theta \right)\propto f\left({\tilde{X}}_i^{\ast }|Y_i^{\ast },C_i^{\ast }\right)$, where ${\tilde{X}}_i^{\ast }|\left(Y_i^{\ast },C_i^{\ast }\right)~N\left(g_i{\gamma }_0+{\gamma }_y{Y}_i^{\ast }+{\gamma }_c^T{C}_i^{\ast },g_i{\sigma }^2+g_i^{2}I\left(g_i>1\right){\sigma }_p^2+g_i^2{\sigma }_m^2\right)$. This derivation differs in a small but important way from that of Lyles et al.¹¹ They assume that errors add to the poolwise sum $X_i^{\ast }$, whereas we take it as more plausible that they add to the poolwise mean ${\overline{X}}_i$ that the assay aims to measure.

We numerically maximize the likelihood to obtain $\widehat{\theta }={\left({\widehat{\gamma }}^T,{\widehat{\sigma }}^2,{\widehat{\sigma }}_p^2,{\widehat{\sigma }}_m^2\right)}^T$, estimate $\widehat{V}\left(\widehat{\theta }\right)$ as the inverse of the estimated Hessian at $\widehat{\theta }$, and calculate the bias-adjusted log-odds ratio using (13). A delta method-based variance estimate for the MLE of the log-odds ratio is $\widehat{V}\left({\widehat{\log -\text{OR}}}_{ml}\right)=f^{\prime }\left(\widehat{\theta }\right)\widehat{V}\left(\widehat{\theta }\right)f^{\prime }{\left(\widehat{\theta }\right)}^T$ with $f^{\prime }\left(\widehat{\theta }\right)=\left(\frac{1}{{\widehat{\sigma }}^2},-\frac{{\widehat{\gamma }}_y}{{\left({\widehat{\sigma }}^2\right)}^2}\right)$. We use this same variance estimator to approximate a standard error for the bias-adjusted log-odds ratio estimator in (13), which should generally be slightly conservative.

2.5 |. Incorporating replicates

For both logistic regression and the discriminant function approach, all parameters are identifiable without replicates, provided the study design includes a sufficient number of different pool sizes. Identifiability requires at least two different pool sizes if ${\tilde{\overline{X}}}_i$ is subject to ME only or PE only and at least three different pool sizes including singles if ${\tilde{\overline{X}}}_i$ is subject to both error types. Still, replicate biomarker measurements can be incorporated into the likelihoods and may help to distinguish ${\sigma }_m^2$ from ${\sigma }_x^2$ and ${\sigma }_p^2$. While replicates could be obtained for pools of any size, we focus on replicate singles.

If for the ith single, we obtain k_i independent replicate assay measurements, ${\tilde{X}}_i={\left({\tilde{X}}_{i1},\dots ,{\tilde{X}}_{i{k}_i}\right)}^T$, the logistic regression likelihood contribution for subject i is the same as in (5) (asterisks omitted since g_i = 1), except ${\tilde{X}}_i$ is vector-valued so the second term under the integral becomes $f\left({\tilde{X}}_i|X_i\right)$. With no processing involved, we assume each ${\tilde{X}}_{ij}$, is the true X_i plus an independent normal measurement error ${\tilde{X}}_i=1_{k_i}{X}_i+{ϵ}_i^m$, ${ϵ}_i^m~N_{k_i}\left(0_{k_i},{\sigma }_m^2{I}_{k_i}\right)$ It follows that

$${\tilde{X}}_i|X_i~N_{k_i}\left(1_{k_i}{X}_i,{\sigma }_m^2{I}_{k_i}\right).$$ (15)

To incorporate replicates for approximate ML, we replace ${\tilde{X}}_i^{\ast }$ in (9) by ${\tilde{X}}_i=1_{k_i}\left({\alpha }_0+{\alpha }_c^T{C}_i+{ϵ}_i^x\right)+{ϵ}_i^m$, leading to corresponding slight modifications of (10) and the subsequent results for $X_i|\left({\tilde{X}}_i,C_i\right)$ and ${\tilde{X}}_i|C_i$.

For the discriminant function approach, the likelihood for a single with replicates is $L_i\left(\theta \right)=f\left({\tilde{X}}_i|Y_i,C_i\right)$. We can write

$$\begin{array}{lll}{\tilde{X}}_i\hfill & =\hfill & 1_{k_i}{X}_i+{ϵ}_i^m=1_{k_i}\left({\gamma }_0+{\gamma }_y{Y}_i+{\gamma }_c^T{C}_i+{ϵ}_i\right)+{ϵ}_i^m\hfill \\ \hfill & =\hfill & 1_{k_i}\left({\gamma }_0+{\gamma }_y{Y}_i+{\gamma }_c^T{C}_i\right)+\left[\begin{array}{cc}{1}_{k_i}& I_{k_i}\end{array}\right]\left[\begin{array}{c}{ϵ}_i\\ {ϵ}_i^m\end{array}\right].\hfill \end{array}$$ (16)

The error vector ${ϵ}_i={\left({ϵ}_i,{ϵ}_i^{m^T}\right)}^T$ is multivariate normal and ${\tilde{X}}_i|\left(Y_i,C_i\right)~N_{k_i}\left(1_{k_i}\left({\gamma }_0+{\gamma }_y{Y}_i+{\gamma }_c^T{C}_i\right),{\sigma }^2{J}_{k_i}+{\sigma }_m^2{I}_{k_i}\right).$ As before, this result implicitly conditions on the covariates C_i.

2.6 |. Implementation

We used R 3.4.3 to develop the package pooling¹⁹ for fitting various models with poolwise data, including those described in this paper.²⁰ The functions p_logreg_xerrors and p_dfa_xerrors implement poolwise logistic regression and the discriminant function approach, respectively, while correcting for PE, ME, both, or neither. Likelihoods are maximized using the nlminb function.²⁰ Initial values and lower and upper bounds for parameters are adjustable; here, we use initial values of 0.01 and bounds of (−∞,∞) for regression coefficients and initial values of 1 and bounds of (0.001,∞) for variance components. Hessian matrices at the MLE’s are numerically approximated via hessian from the pracma package.²¹ The logistic regression function supports both full ML and approximate ML.

For full ML, numerical integration is implemented via the adaptlntegrate function in the R package cubature,²² which itself relies on the C function hcubature in the C package cubature.²³ The latter function uses h-adaptive integration, which partitions the integration region into subregions, applies an integration rule to each subregion to obtain an integral estimate and error estimate, targets the region with the largest error for further partitioning, and continues until the total error is below a specified cutpoint.²⁴ Further details on the algorithm are provided by Berntsen et al²⁵ and Genz and Malik.²⁶ We used a change of variables transformation to integrate over the finite interval (−1, 1).

3 |. COLLABORATIVE PERINATAL PROJECT

The Collaborative Perinatal Project (CPP) was a multisite prospective study initiated in 1959 and aimed at identifying risk factors for maternal and infant mortality and cerebral palsy.²⁷ A later nested case-control study was conducted to test whether serum cytokine levels during pregnancy were associated with risk of spontaneous abortion (SA).²⁸ We use data from the follow-up study, in which cytokines were measured in singles and pools of size 2 using stored serum samples from the original CPP study. Our aim is to assess whether the cytokine monocyte chemotactic protein (MCP-1) is associated with risk of SA, controlling for age, race, and smoking. The data consist of 96 singles without replicates (g_i = 1, k_i = 1) and 30 singles with two replicates (g_i = 1, k_i = 2), and 280 pools of size 2 (g_i = 2, k_i = 1), for a total of 686 participants and 436 measurements.

Table 1A shows covariate-adjusted log-odds ratio estimates for the corrective methods without incorporating replicates, ie, using just one (randomly selected) of the two MCP-1 measurements for the 30 observations with replicates (LRF = logistic regression with full ML, LRA = logistic regression with approximate ML, DFA = discriminant function approach). Cell values indicate $\widehat{\beta }\left(SE\right)$, AIC, with β representing the effect of a 0.1-ng/mL change in MCP-1 on log-odds of SA, and lower AIC indicating better fit relative to models in the same row.²⁹

TABLE 1.

Estimates of the covariate-adjusted log-odds ratio for MCP-1 and spontaneous abortion, without (A) and with (B) the 30 replicate MCP-1 measurements incorporated. Values are estimated log-odds ratio (standard error), Akaike information criterion

		(A) Error Type
Method	Neither	PE only	ME only	PE and ME
LRF	0.012 (0.024), 2822.0	0.070 (0.115), 2697.6	−0.071 (−), 2762.4b	Not identifiable
LRA	n/aa	0.071 (0.115), 2697.5	−0.088 (−), 2762.4b	Not identifiable
DFA	0.016 (0.025), 2277.6	0.090 (0.114), 2153.0	∞ (−), 2217.7c	Not identifiable
		(B) Error Type
	Neither	PE only	ME only	PE and ME
LRF	n/ad	n/ad	0.026 (0.049), 2353.8	0.046 (0.082), 2340.8
LRA	n/ad	n/ad	0.026 (0.049), 2353.8	0.046 (0.082), 2340.8
DFA	n/ad	n/ad	0.030 (0.051), 1809.5	0.050 (0.081), 1796.5

^aThere is no integral to approximate because assuming neither error type means MCP-1 is precisely measured.

^bEstimate of residual error variance in MCP-1 given covariates model hit lower bound of 0.001. Standard error omitted because variance-covariance matrix not positive definite.

^cEstimate of residual error variance in discriminant function model hit lower bound of 0.001, causing “blow-up” in log-OR estimate.

^dCannot fit with replicates because no ME would imply that two distinct values are both the true MCP-1.

DFA, discriminant function approach; LRA, logistic regression with approximate maximum likelihood; LRF, logistic regression with full maximum likelihood; MCP-1, monocyte chemotactic protein-1; ME, measurement error; OR, odds ratio; PE, processing error.

Without replicates, models with both PE and ME could not be fit; an additional pool size would have been necessary for identifiability. This is an important limitation because it means choosing from three candidate models that may all inadequately correct for MCP-1 errors. AIC favored PE only for all three corrective methods. ME-only models had lower AIC than neither but produced clearly implausible parameter estimates (eg, residual error variances hitting lower bounds of 0.001). Logistic regression was particularly unstable for ME only; different starting values produced very different $\widehat{\beta }’\text{s}$ but similar maximized log-likelihoods (not shown). Relative to neither-error models, PE-only models had larger point estimates but also larger standard errors, such that the association between MCP-1 and SA still did not approach statistical significance.

Estimation after incorporating the second MCP-1 measurement for the 30 observations with replicates is summarized in Table 1B. Note that the neither-error and PE-only models cannot incorporate replicates because no ME is incompatible with observing two nonidentical MCP-1 measurements for the same specimen (eg, (15) with ${\sigma }_m^2=0$ implies ${\tilde{X}}_{i1}={\tilde{X}}_{i2}=X_i$). AIC favored PE and ME for all three methods. The estimated variance components for LRF were ${\widehat{\sigma }}_x^2=1.580,$ ${\widehat{\sigma }}_p^2=0.729,$ ${\widehat{\sigma }}_m^2=\mathrm{0.108.}$ Relatively small ME variance is reasonable given the high correlation between the 30 replicate MCP-1 measurements (r = 0.976).

Table 2 summarizes the LRF fit with replicates incorporated and accounting for both error types alongside the naive poolwise logistic regression fit ignoring errors in MCP-1. Both model fits suggest that older age, nonwhite race, and current smoking are associated with higher odds of SA. The covariate-adjusted association between MCP-1 and SA was not statistically significant in either case, but the odds ratio was slightly higher in the error-adjusted model.

TABLE 2.

Logistic regression fits for risk of spontaneous abortion

	Ignoring MCP-1 errors			Accounting for MCP-1 errors
Variable	Beta (SE)	OR (95% CI)	p-value	Beta (SE)	OR (95% CI)	p-value
Intercept	−1.565 (0.372)	-	< 0.001	−1.581 (0.374)	-	< 0.001
MCP-1 (Δ 0.1 ng/mL)	0.012 (0.024)	1.012 (0.966, 1.060)	0.62	0.046 (0.082)	1.047 (0.891, 1.230)	0.58
Mother’s age	0.037 (0.013)	1.037 (1.011, 1.064)	0.005	0.036 (0.013)	1.037 (1.011, 1.064)	0.006
Non-white race	0.560 (0.175)	1.751 (1.242, 2.470)	0.001	0.566 (0.176)	1.761 (1.247, 2.488)	0.001
Current smoking	0.338 (0.162)	1.402 (1.021, 1.926)	0.04	0.338 (0.162)	1.402 (1.021, 1.926)	0.04

CI, confidence interval; MCP-1, monocyte chemotactic protein-1; OR, odds ratio; SE, standard error.

4 |. SIMULATION STUDIES

We performed simulations modeled after the CPP data to confirm validity of the error-correction methods, assess robustness to non-normal errors, and compare the efficiency of traditional vs pooling study designs as a function of PE and ME.

The main assumption underlying the discriminant function approach (normal linear regression for X_ij|(Y_ij, C_ij)) implies logistic regression, whereas the assumptions underlying the logistic regression method (homogeneous pools, logistic regression for Y_ij|(X_ij, C_ij), linear regression for X_tj|C_ij) do not necessarily imply the discriminant function model. Because our main focus is logistic regression, where odds ratios for all predictors rather than just the pooled exposure can be estimated, we generate data under logistic regression. The discriminant function approach is therefore more of a working model for the data.

Covariates generated independently include mother’s age, C_1ij ∈ (14, … , 45) with sampling probabilities matching the CPP age distribution; nonwhite race, C_2ij~Bernoulli(0.34); and smoking, C_3ij~Bernoulli(0.47). Using estimates from the full-ML logistic regression with both error types and replicates, MCP-1 in 10 ng/mL (X_ij) given covariates is a linear regression with (α₀, α_c1, α_c2, α_c3, ${\sigma }_x^2$) = (0.50, 0.03,−0.17, 0.02, 1.58), and SA (Y_ij) given MCP-1 and covariates is a logistic regression with (β₀, β_x, β_c1, β_c2, β_c3) = (−1.58, 0.20,0.04, 0.57, 0.34). The estimated log-odds ratio for MCP-1 was 0.046, but we use 0.20 to simulate a moderate effect where a 0.1-ng/mL increment in MCP-1 increases odds of SA as much as a five-year increment in mother’s age. Error variances were set to ${\sigma }_p^2=0.73$ and ${\sigma }_m^2=\mathrm{0.11.}$

4.1 |. Validity of error-correction methods

The first set of simulations is intended to assess validity of the error-correction methods for a design comprised of an approximately equal number of pools of size 1, 2, and 3. For each trial, we generate 686 values for (C_1ij, C_2ij, C_3ij, X_ij, Y_ij) and split the data into n1 cases and n0 controls. Within the cases, we form $\frac{n_1}{6}$ (rounded up) pools of size 2 and 3 and leave the remaining observations as singles and similarly for controls. For the error-prone poolwise exposure, we calculate the poolwise mean ${\overline{X}}_i,$ add normal errors to obtain the imprecise poolwise mean $\stackrel{\simeq }{X_i},$ and multiply by the pool size to obtain the imprecise poolwise sum ${\tilde{X}}_i^{*}.$ We calculate poolwise sums for covariates to obtain the full poolwise vector (Y_i, ${\tilde{X}}_i^{*},$ $C_{i1}^{*},$ $C_{i2}^{*},$ $C_{i3}^{*}$). For scenarios with replicates, ${\tilde{X}}_i={\left({\tilde{X}}_{i1},{\tilde{X}}_{i2}\right)}^T$ is generated by adding two independent measurement errors to X_i.

Table 3 summarizes performance of the three methods and naive poolwise logistic regression for PE only, ME only, and both. Error type refers to both data generation and estimation, such that LRF, LRA, and DFA are correctly specified in each scenario.

TABLE 3.

Simulation results for estimation of covariate-adjusted log-odds ratio relating MCP-1 and spontaneous abortion (2500 trials, true value = 0.20)

	Mean Bias (Median Bias)	SD(IQR)	Mean SE	MSE	95% CI Coverage
PE only
Logistic regression ignoring MCP-1 errors	−0.097	0.047	0.047	0.012	0.447
LRF	0.014	0.099	0.099	0.010	0.958
LRA	0.013	0.099	0.098	0.011	0.958
DFA	0.005	0.092	0.094	0.009	0.959
ME only
Without replicatesa
Logistic regression ignoring MCP-1 errors	−0.025	0.064	0.062	0.005	0.919
LRF	0.027	0.108	0.104	0.012	0.970
LRA	0.027	0.107	0.104	0.012	0.970
DFA	0.003	0.084	0.095	0.007	0.970
With replicates
LRF	0.005	0.076	0.074	0.006	0.954
LRA	0.004	0.076	0.074	0.006	0.954
DFA	0.001	0.074	0.073	0.005	0.954
PE and ME
Without replicates
Logistic regression ignoring MCP-1 errors	(−0.106)	(0.061)	-	-	0.355
LRF	(0.062)	(0.306)	-	-	0.987c
LRA	(0.062)	(0.302)	-	-	0.987d
DFAb	(0.053)	(0.290)	-	-	0.986
With replicates
LRF	0.014	0.103	0.103	0.011	0.962
LRA	0.013	0.102	0.102	0.011	0.962
DFA	0.005	0.095	0.098	0.009	0.964

^aExcludes 2 trials in which LRF produced extreme log-OR estimates (>2).

^bnon-bias-adjusted version of estimator used because bias adjustment frequently flipped sign of log-OR estimate (74.8% of trials).

^cExcludes 70 trials in which variance-covariance matrix was not positive definite.

^dExcludes 79 trials in which variance-covariance matrix was not positive definite.

CI, confidence interval; DFA, discriminant function approach; IQR, interquartile range; LRA, logistic regression with approximate maximum likelihood; ME, measurement error; OR, odds ratio; PE, processing error; SD, standard deviation; SE, standard error; MSE, mean squared error.

In the PE-only scenario, naive logistic regression exhibited substantial downward bias and low CI coverage, suggesting that PE is too large to ignore. The corrective methods performed reasonably well, although LRF and LRA had some upward bias. Despite generating data under logistic regression, DFA had slightly less bias and better efficiency than LRF and LRA.

In the ME-only scenario, naive logistic regression exhibited a small amount of downward bias and slightly lower than nominal CI coverage, suggesting that ME was nearly small enough to ignore. Without replicates, LRF and LRA exhibited upward bias of about the same magnitude as the naive approach, whereas DFA was virtually unbiased and more efficient. The ME variance estimate ${\widehat{\sigma }}_m^2$ hit its lower bound of 0.001 in 23.5% of trials for both LRF and LRA and 27.7% of trials for DFA. Replicates improved estimation; for all three methods, ${\widehat{\sigma }}_m^2$ never hit 0.001, bias was reduced and efficiency improved, and CI coverage was closer to nominal.

In the PE and ME scenario, performance without replicates was poor. The corrective methods often produced extreme estimates ($\widehat{\log -OR}$ outside of [−1, 1] in 13.1% of trials for LRF, 12.6% for LRA, 13.9% for DFA) and exhibited upward median bias. At least one variance component estimate hit 0.001 in the majority of trials for all three methods (LRF: ${\widehat{\sigma }}_x^2$ 0.1%, ${\widehat{\sigma }}_p^2$ 16.8%, ${\widehat{\sigma }}_m^2$ 48.0%; LRA: ${\widehat{\sigma }}_x^2$ 0.1%, ${\widehat{\sigma }}_p^2$ 16.9%, ${\widehat{\sigma }}_m^2$ 47.8%; DFA: ${\widehat{\sigma }}^2$ 4.8%, ${\widehat{\sigma }}_p^2$ 20.3%, ${\widehat{\sigma }}_m^2$ 48.2%). Adding replicates resolved this issue and drastically improved estimation.

The stabilizing role of replicates in the PE and ME scenario is illustrated by the $\widehat{\log -OR}$ histograms in Figure 1. While the log-odds ratio is identifiable with pools of size 1, 2, and 3 and no replicates, estimation is relatively unstable even for a fairly large sample size. We note that log-odds ratio estimates outside of [−1, 1] remained fairly common even after a five-fold increase to n = 3,430 (1000 trials: 2.9% for LRF, 3.6% for LRA, 2.9% for DFA).

FIGURE 1.

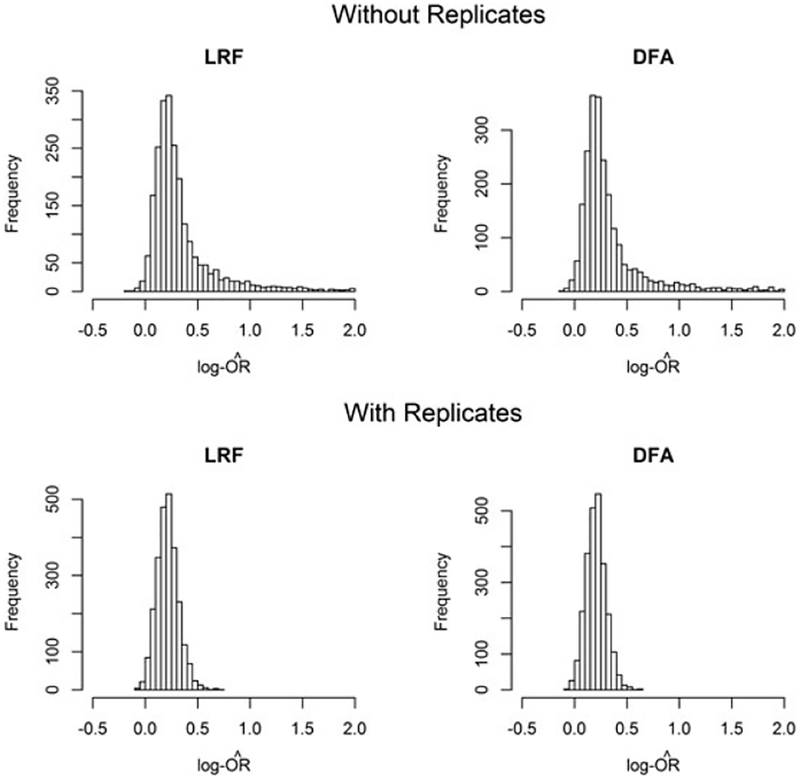
Distribution of log-odds ratio estimates in simulations with processing error and measurement error (2500 trials, true value = 0.2). DFA, discriminant function approach; LRF, logistic regression with full maximum likelihood

4.2 |. Robustness to non-normality of errors

To assess performance under misspecification of the error distribution, we repeated the previous simulations with errors distributed lognormal (shifted to mean 0) rather than normal. Processing errors were generated as LN(0.925, 0.099) minus 2.6498 and measurement errors LN(−0.022, 0.099) minus 1.0279, which correspond to skewness = 1 and the same variances as in the normal-errors scenario (0.73 and 0.11). Results are summarized in Table 4. All three methods performed well despite modeling right-skewed lognormal errors as normal; performance metrics were extremely similar to the normal-errors results in Table 3. Performance was also similar with errors uniformly distributed with mean 0 and variances 0.73 and 0.11 (not shown).

TABLE 4.

Simulation results for estimation of covariate-adjusted log-odds ratio relating MCP-1 and spontaneous abortion, with errors distributed lognormal (shifted to mean 0) with skewness of 1 and the same variance as in the normal-errors case (2500 trials, true value = 0.20)

	Mean Bias (Median Bias)	SD(IQR)	Mean SE	MSE	95% CI Coverage
PE only
Logistic regression ignoring MCP-1 errors	−0.097	0.050	0.048	0.012	0.458
LRF	0.012	0.102	0.099	0.011	0.956
LRA	0.012	0.101	0.099	0.010	0.956
DFA	0.004	0.094	0.094	0.009	0.960
ME only
Without replicates
Logistic regression ignoring MCP-1 errors	−0.024	0.064	0.063	0.005	0.921
LRF	0.028	0.109	0.104	0.013	0.969
LRA	0.027	0.107	0.103	0.012	0.969
DFA	0.004	0.085	0.094	0.007	0.964
With replicates
LRF	0.006	0.077	0.074	0.006	0.950
LRA	0.006	0.077	0.074	0.006	0.949
DFA	0.003	0.074	0.073	0.006	0.951
PE and ME
Without replicates
Logistic regression ignoring MCP-1 errors	(−0.106)	(0.062)	-	-	0.362
LRF	(0.067)	(0.366)	-	-	0.984b
LRA	(0.066)	(0.359)	-	-	0.985c
DFAa	(0.060)	(0.348)	-	-	0.984
With replicates
LRF	0.016	0.109	0.104	0.012	0.959
LRA	0.015	0.108	0.103	0.012	0.959
DFA	0.007	0.100	0.099	0.010	0.956

^anon-bias-adjusted version of estimator used because bias adjustment frequently flipped sign of log-OR estimate (76.0% of trials).

^bExcludes 88 trials in which variance-covariance matrix was not positive definite.

^cExcludes 99 trials in which variance-covariance matrix was not positive definite.

CI, confidence interval; DFA, discriminant function approach; IQR, interquartile range; LRA, logistic regression with approximate maximum likelihood; ME, measurement error; OR, odds ratio; PE, processing error; SD, standard deviation; SE, standard error; MSE, mean squared error.

4.3 |. Efficiency of traditional vs. pooling designs

The purpose of the next set of simulations is to compare the efficiency of various designs as a function of PE and ME, holding the total number of assays fixed at 900. For each trial, we generate 50 000 individual-level values (C_1ij, C_2ij, C_3ij, ${\tilde{X}}_{ij}^{*},$ Y_ij with the same data generating process as in the prior simulations. For the traditional design, we sample 450 cases and 450 controls. For the first pooling design (“P-1-2-3”), we sample 900 cases and form 450 pools, 150 with g_i = 1, 150 with g_i = 2, and 150 with g_i = 3, and similarly for controls. For the second, more aggressive pooling design (“P-1–5”), we sample 1650 cases and form 450 pools, 150 with g_i = 1 and 300 with g_i = 5, and similarly for controls. In scenarios with ME, the traditional design requires replicates for validity, so we randomly select 50 observations for which to generate two exposure measurements and 50 to exclude to keep the assay count at 900. We also incorporate 50 replicates into both pooling designs in scenarios with ME.

Figure 2 compares efficiency of traditional and pooling designs for the LRA and DFA methods (LRF omitted; Pearson r > 0.998 for LRF and LRA in first 25 trials for all scenarios). The width of the middle 80% of estimates (ie, the difference between the 90th and 10th percentile) was chosen as a measure of variability to lessen the impact of extreme estimates. Trends for pooling vs traditional designs were generally similar for LRA (left column) and DFA (right). For PE only (top panel), the pooling designs were highly efficient for small PE, but that advantage eroded and eventually reversed as ${\sigma }_p^2$ increased. For ME only with replicates (middle) and both PE and ME with replicates (bottom), the efficiency advantage was reduced with increasing ME, but the pooling designs did not become clearly counterproductive even for large ${\sigma }_m^2.$ Notably, DFA was more efficient than LRA in all 54 scenarios.

FIGURE 2.

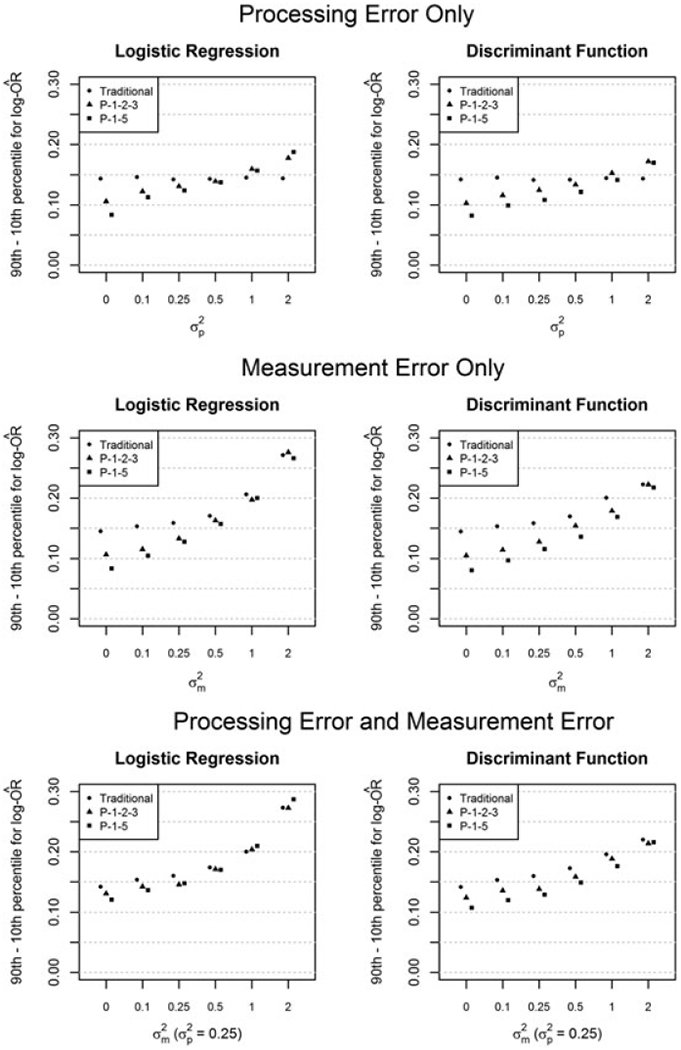
Width of middle 80% of log-odds ratio estimates (5000 trials each)

5 |. DISCUSSION

Prior researchers^4,7 developed a homogeneous-pools logistic regression model that provides an analytic method to accompany a cost-effective pooling design, which can be used in any scenario where outcomes are observed prior to measuring exposure (eg, cross-sectional and case-control studies and cohort studies with stored specimens). However, fitting this model without accounting for potential errors in the poolwise exposure measurements can lead to bias. Validity requires not only that the assay has negligible measurement error but also that each value it returns is exactly the arithmetic mean exposure for members of a pool. In reality, handling and combining samples in the laboratory may lead to extra variability that cannot be ignored.

In general, the corrective methods we examined to correct for errors produced valid estimates of covariate-adjusted log-odds ratios. Our updates to a proposed discriminant function approach¹¹ tended to give less biased and in some cases considerably more efficient estimates of the exposure log-odds ratio than the newly developed logistic regression approach based on full or approximate ML in simulations despite generating data under logistic regression. The bias adjustment incorporated into the discriminant function approach (eg, in (13)) likely explains some of this difference as logistic regression is prone to small-sample bias away from the null.^30,31 Nevertheless, we suspect analysts may still prefer logistic regression given that it is the more familiar and general of the two and yields log-odds ratio estimates for all covariates rather than just the pooled exposure. Both methods can theoretically correct for both PE and ME as long as there are at least three different pool sizes including 1, but we find that adding replicate single measurements drastically improves stability when both error types are present.

For logistic regression, full and approximate ML produced very similar parameter estimates for the CPP dataset and had extremely similar performance in simulations. Full ML is much slower because it requires numerical integration for each pool at each iteration of likelihood maximization. For our Table 3 simulations with both error types and replicates, each trial took approximately 5 minutes for full ML and only about 3 seconds for approximate ML. In practice, investigators with poolwise data could fit both versions, confirm that estimates are similar, and report the full ML results. Comparing parameter estimates and maximized log-likelihoods might also be helpful in detecting numerical issues with full ML when they occur.

Our approaches are fully parametric and thus potentially susceptible to validity issues when assumptions are violated. Simulations suggested considerable robustness to non-normal errors, but the error distributions we tested were still mean 0 and additive. If normality assumptions are clearly violated, one could consider using our full ML logistic regression framework with a different measurement error model and/or exposure model. However, alternative exposure models (eg, a log-transformed linear regression) will typically not have a convenient poolwise sum result like linear regression.³² The discriminant function approach could also be used with nonormal errors, but it would likely not have a closed-form likelihood.

One question raised by a reviewer is whether data from a homogeneous pools design could be used to analyze a secondary outcome. Associations with other variables conditional on the original outcome could be explored. For example, one could compare mean biomarker level by sex within case pools and within control pools and perhaps combine estimates if they are similar. However, estimating unconditional associations would likely require adapting special methods like those proposed by Tchetgen Tchetgen³³ and Reilly et al³⁴ to the pooling context. In terms of our methodology, the logistic regression methods would not be usable for a secondary outcome because pools would no longer be homogeneous. The discriminant function approach could still be used, however; fitting it separately for cases and controls would produce two odds ratio estimates, whereas fitting it with case status as a covariate would be akin to adjusting for the original outcome variable. Other methods compatible with heterogeneous pools^35,36 could also be used, although most cannot correct for errors in the pooled biomarker.

Our methods assume that errors in the pooled exposure have the same form for those experiencing and not experiencing the outcome. While this nondifferential ME assumption may be considered dubious when exposure levels are self-reported,^8,37 it appears reasonable for assay-based exposure assessment. It seems unlikely that assay errors would differ by case status (differential ME) or that case samples and control samples might be handled in a way that induces different amounts of extra variability to each (differential PE). The latter could perhaps occur in scenarios where new controls are matched to case samples that have been stored for an extended period of time.

One way to relax the nondifferential error assumption is to allow the processing and/or measurement errors to have different variances in case pools and control pools. While this would nullify the discriminant function approach’s advantage of not requiring homogeneous pools, the pooling design lacks efficiency in that scenario anyway.¹¹ We have included an option to allow for differential PE and/or ME in our publicly available R functions.

A similar concern is whether it is reasonable to assume that the PE variance is independent of pool size. If caused by factors such as unequal specimen volumes and cross-reactions among samples from different people, PE may be more severe in larger pools. We suggest two potential solutions. First, one can avoid the problem entirely with a study design that includes singles and pools of just one other size such as the P-1–5 design. The models discussed herein would account for whatever PE affects the pooled observations; it would not matter whether pools of other sizes would have been subject to larger or smaller errors. Second, one could specify a relationship between pool size and PE variance. One simple approach currently supported in our R functions is to assume the assay returns the poolwise mean plus a normal PE times $\sqrt{\frac{g_i}{2}}I\left(g_i>1\right)$ (plus the ME, if applicable). This reflects an assumption that the PE variance increases at the same rate as pool size so that, for example, a pool with twice the number of members is subject to PE with twice the variance. Other more flexible approaches are also possible, eg, a linear relationship between pool size and PE variance with a nonunity slope estimated from the data.

A brief note on identifiability in the absence of replicates is warranted as our assessment differs slightly from those of prior authors.^10,11 Returning to the original set of assumptions (nondifferential errors, PE variance independent of pool size), the variance of the error-prone poolwise sum exposure given covariates is $g_i{\sigma }_x^2+g_i^2{\sigma }_p^{2}I\left(g_i>1\right)+g_i^2{\sigma }_m^2.$ With ME only, two pool sizes g₁ and g₂ result in variances $g_1{\sigma }_x^2+g_1^2{\sigma }_m^2$ and $g_2{\sigma }_x^2+g_2^2{\sigma }_m^2,$ respectively. For any two distinct pool sizes (g₁, g₂), these quantities are not equal nor multiples of each other, so ${\sigma }_x^2$ and ${\sigma }_m^2$ are identified. The situation is the same with PE only: at least two different pool sizes are required, and neither has to be 1.¹¹ With both error types, we agree that at least three different pool sizes, including 1, are required to identify all parameters.^10,11 However, two pool sizes not including 1 is sufficient to identify ${\sigma }_x^2$ and the sum $\left({\sigma }_p^2+{\sigma }_m^2\right),$ which, in theory, is enough to achieve the primary goal of removing bias due to both error types. If replicate singles are included in the study design, identifiability is guaranteed regardless of what pool sizes are included.

The fact that two pool sizes other than 1 is sufficient to correct for both error types, while not bothering to distinguish them, is initially encouraging. It suggests a way to get around stability issues that arise when both errors are present and there are no replicates. In this scenario, each poolwise measurement is subject to a normal PE and a normal ME, which can be viewed as a single mean 0 normal error with variance ${\sigma }_p^2+{\sigma }_m^2.$ This is no different than a PE-only scenario with PE variance ${\sigma }_p^2+{\sigma }_m^2,$ so we might expect similar stability. Unfortunately, adequate stability in PE-only simulations is aided by the very presence of singles, which are not subject to PE and thus help distinguish ${\sigma }_x^2$ from ${\sigma }_p^2.$ In simulations not included here, we were unable to find a scenario where a P-2–3 design was advantageous over P-1-2-3. Still, it is noteworthy that correcting for both error types is possible if one encounters poolwise data with two pool sizes not including 1.

Next, we turn to the central question of whether a pooling design remains cost effective in the presence of errors. In a two-sample t-test scenario, a pooling design where each measurement is the arithmetic mean for g_i members of a group is efficient because each measurement has variance $\frac{{\sigma }^2}{g_i}$ rather than σ². The ratio of variances for pooled measurements to individual measurements is $\frac{1}{g_i},$ so the optimal design for a fixed number of assays is one very large pool size. Theoretically, a large enough pool size could provide power of virtually 1 for any fixed number of assays.

With errors, the variance of each measurement in the traditional design is ${\sigma }^2+{\sigma }_m^2$ and, in the pooling design, is $\frac{{\sigma }^2}{g_i}+{\sigma }_p^2+{\sigma }_m^2.$ The ratio is $V_{p:t}=\frac{1}{{\sigma }^2+{\sigma }_m^2}\left(\frac{{\sigma }^2}{g_i}+{\sigma }_p^2+{\sigma }_m^2\right),$ which is minimized for ${\sigma }_p^2={\sigma }_m^2=0.$ Thus, PE and ME both have the effect of reducing the efficiency advantage of a pooling design.

If there is PE only, $V_{p:t}=\frac{1}{g_i}+\frac{{\sigma }_p^2}{{\sigma }^2}$ which converges to $\frac{1}{g_i}$ as ${\sigma }_p^2\to 0,\infty$ as ${\sigma }_p^2\to \infty ,$ and $\frac{1}{g_i}+1$ as ${\sigma }_p^2\to {\sigma }^2.$ We note that $V_{p:t}>1\text{ if }{\sigma }_p^2>{\sigma }^2\left(1-\frac{1}{g_i}\right),$ meaning that, for example, if the biggest pool size possible is 5, a poolwise design will be less efficient than a traditional design if ${\sigma }_p^2$ is more than 80% of σ². For ME only, $V_{p:t}=\frac{\frac{{\sigma }^2}{g_i}+{\sigma }_m^2}{{\sigma }^2+{\sigma }_m^2}$ which converges to $\frac{1}{g_i}$ as ${\sigma }_m^2\to 0,1$ as ${\sigma }_m^2\to \infty ,$ and $0.5<\frac{1+g_i}{2g_i}<1$ as ${\sigma }_m^2\to {\sigma }^2.$ Thus, for PE only, a pooling design can become counterproductive if ${\sigma }_p^2$ is nearly as large or larger than σ², but for ME only, a pooling design should remain more efficient even if ${\sigma }_m^2$ is as large as σ². With both PE and ME, results are generally the same as for PE only, but the added measurement error will make any efficiency advantage smaller than it would have been with only PE and the same ${\sigma }_p^2.$

While our analytic framework is somewhat different (ie, the models are more involved, covariates are present, and the variance terms have to be estimated), our simulations (see Figure 2) mostly agreed with efficiency results predicted by the above t-test-based arguments.

In summary, we have provided a method to correct for errors that can compromise validity of homogeneous-pools logistic regression. The pooling study design should remain cost effective in situations where the assay is expensive and relatively precise, and careful handling can keep processing errors to a minimum. In future work, we plan to further generalize the methods presented here to accommodate non-normal errors and skewness in the pooled biomarker. Developing methods to handle potential sources of bias in pooling studies should lead to more feasible implementation of this very promising study design.