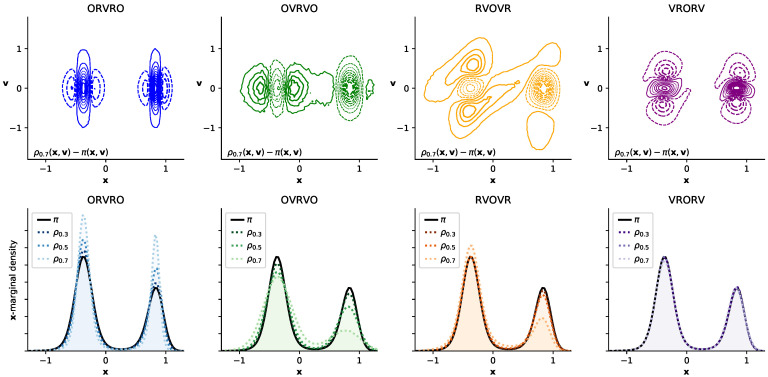
Figure 1.

Different numerical integrators introduce different error structure in phase space, illustrated in a double-well system. Here, we illustrate the timestep-dependent discretization error introduced by four integrators on a 1D double-well potential [$U\left(\mathbf{x}\right)\equiv {\mathbf{x}}^6+2cos\left(5(\mathbf{x}+1)\right)$]. The top row of 2D contour plots illustrates the difference between the phase-space density $\rho (\mathbf{x},\mathbf{v})$ sampled at the maximum timestep considered ($\Delta t=0.7$, close to the stability limit) and the equilibrium density $\pi (\mathbf{x},\mathbf{v})$; solid lines indicate positive contours, while dashed lines indicate negative contours. The bottom row of 1D density plots shows timestep-dependent perturbation in the sampled marginal distribution in configuration space, ${\rho }_{\mathbf{x}}$, with the equilibrium distribution ${\pi }_{\mathbf{x}}$ depicted as a solid black line. The sampled marginal distributions ${\rho }_{\mathbf{x}}$ are shown for increasingly large timestep, denoted ${\rho }_{\Delta t}$, depicted by increasingly light dotted lines, for $\Delta t=0.3,0.5,0.7$ (arbitrary units). Inspecting the contour plots suggests that some integrator splittings (especially VRORV) induce error that fortuitously “cancels out” when the density is marginalized by integrating over $\mathbf{v}$, while the error in other integrator splittings (ORVRO, OVRVO) constructively sums to amplify the error in configuration space.