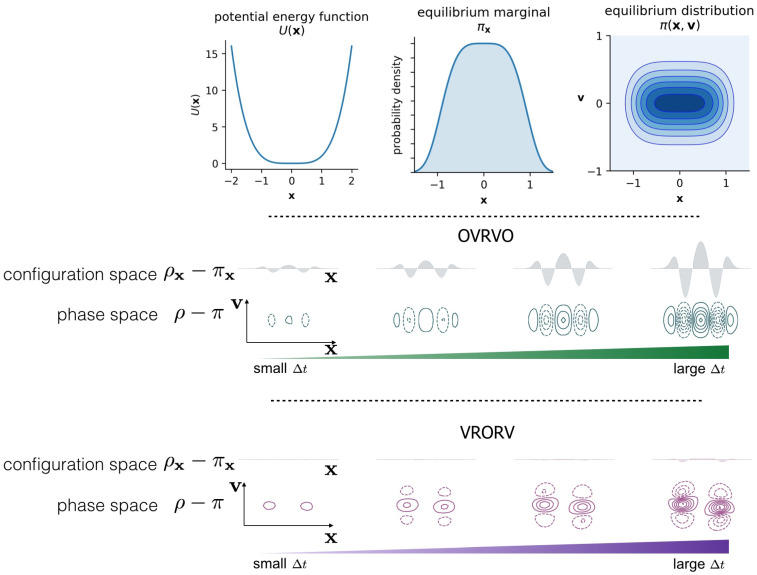
Figure 3.

Comparison of Langevin integrators in terms of phase-space and marginal distributions. For a simple 1D system with the quartic potential $U\left(\mathbf{x}\right)={\mathbf{x}}^4$, the error in sampled phase-space density $\rho$ and its marginal density ${\rho }_{\mathbf{x}}$ grows as a function of timestep $\Delta t$. However, different Langevin integrators (OVRVO and VRORV shown here) derived from symmetric Strang splittings can lead to drastically different error structures in phase space, which can induce fortuitous cancellation of error in the marginal distribution under certain circumstances (VRORV), see [18]. In the top row, we illustrate the definition of the 1D system (left: the potential energy function, $U\left(\mathbf{x}\right)={\mathbf{x}}^4$; middle: the equilibrium marginal density over configuration space, ${\pi }_{\mathbf{x}}\left(\mathbf{x}\right)\propto e^{-\beta U\left(\mathbf{x}\right)}$; right: the equilibrium joint distribution over phase space $\pi (\mathbf{x},\mathbf{v})$). In the middle row, we illustrate the increasing discrepancy between the sampled distribution ρ and the equilibrium distribution π, for both the full phase-space and the marginal configuration space, as a function of timestep $\Delta t$, for the given model problem and the particular choice of the Bussi–Parinello Langevin integrator OVRVO (7). Here the differences between exact and discrete configurational measures are plotted above the contours of the phase space density, for four values of the stepsize $\Delta t=$ [0.43, 0.66, 0.88, 1.1]. In the bottom row, we illustrate the timestep-dependent error in a similar way for another integrator VRORV (12).