Figure 1.

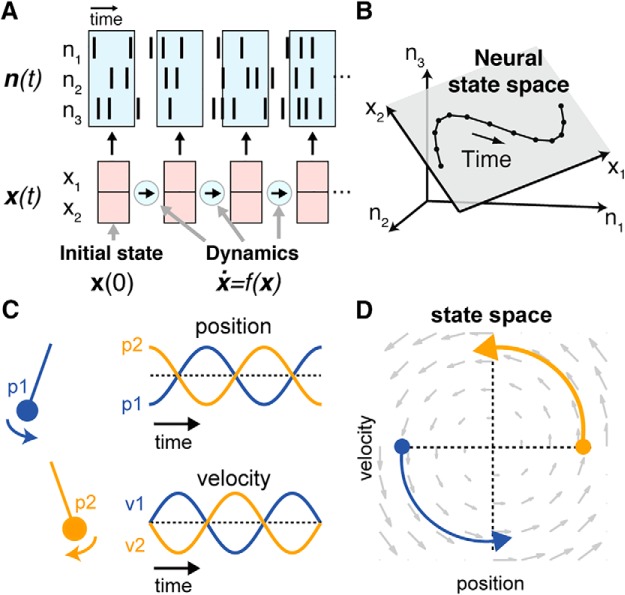
Intuition for latent factors and dynamical systems. A, n(t) is a vector representing observed spiking activity. Each element of the vector captures the number of spikes a given neuron emits within a short time window around time t. n(t) can typically be captured by the neural state variable x(t), an abstract, lower-dimensional representation that captures the state of the network. Dynamics are the rules that govern how the state updates in time. For a completely autonomous dynamical system without noise, if the dynamics f(x) are known, then the upcoming states are completely predictable based on an initial state x(0). B, In a simple three-neuron example, the ensemble's activity at each point in time traces out a trajectory in a 3-D state space, where each axis represents the activity of a given neuron. Not all possible patterns of activity are observed, rather, activity is confined to a 2-D plane within the 3-D space. The axes of this plane represent the neural state dimensions. Adapted from Cunningham and Yu, 2014. C, Conceptual low-dimensional dynamical system: a 1-D pendulum. A pendulum released from point p1 or p2 traces out different positions and velocities over time, and the state of the system can be captured by two state variables (position and velocity). D, The evolution of the system over time follows a fixed set of dynamic rules, i.e., the pendulum's equations of motion. Knowing the pendulum's initial state [x(0), filled circles] and the dynamical rules that govern its evolution [f(x), gray vector flow-field] is sufficient to predict the system's state at all future time points.