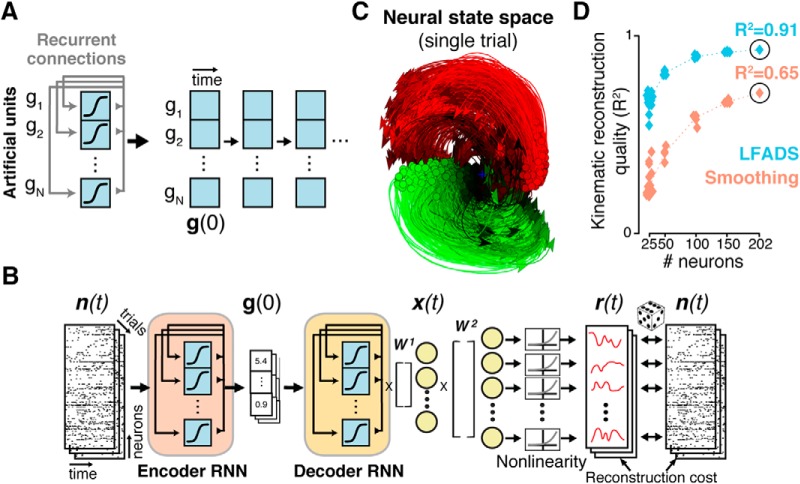
Figure 4.

LFADS uses recurrent neural networks to infer precise estimates of single-trial population dynamics. A, A recurrent neural network (simplified) is a set of artificial neurons that implements a nonlinear dynamical system, with dynamics set by adjusting the weights of its recurrent connections. Conceptually, the RNN can be “unrolled” in time, where future states of the RNN are completely predicted based in an initial state g(0) and its learned recurrent connectivity (compare Fig. 3A). B, The SAE framework consists of an encoding network and decoding network. The encoder (RNN) compresses single-trial observed activity n(t) into a trial code g(0), which sets the initial state of the decoder RNN. The decoder attempts to re-create n(t) based only on g(0). To do so, the decoder must model the ensemble's dynamics using its recurrent connectivity. The output of the decoder is x(t), the latent factors, and r(t), the de-noised firing rates. C, The de-noised single-trial estimates produced by LFADS uncover known dynamic features (such as rotations; Fig. 2A) on single trials. D, Decoding the LFADS-de-noised rates using simple optimal linear estimation leads to vastly improved predictions of behavioral variables (hand velocities) over Gaussian smoothing, even with limited numbers of neurons. Adapted from Pandarinath et al., 2018.