Error Bars Considered Harmful: Exploring Alternate Encodings for Mean and Error

Abstract

When making an inference or comparison with uncertain, noisy, or incomplete data, measurement error and confidence intervals can be as important for judgment as the actual mean values of different groups. These often misunderstood statistical quantities are frequently represented by bar charts with error bars. This paper investigates drawbacks with this standard encoding, and considers a set of alternatives designed to more effectively communicate the implications of mean and error data to a general audience, drawing from lessons learned from the use of visual statistics in the information visualization community. We present a series of crowd-sourced experiments that confirm that the encoding of mean and error significantly changes how viewers make decisions about uncertain data. Careful consideration of design tradeoffs in the visual presentation of data results in human reasoning that is more consistently aligned with statistical inferences. We suggest the use of gradient plots (which use transparency to encode uncertainty) and violin plots (which use width) as better alternatives for inferential tasks than bar charts with error bars.

1. Introduction

For judgments and comparisons in real world settings, the uncertainty associated with the data can be as important as the difference in data values. Big differences in data values may not be significant or interesting if there is too much error: for instance too much noise, uncertainty, or spread. Techniques from inferential statistics (including comparison of interval estimates, null hypothesis significance testing, and Bayesian inference) address this issue, but can be complicated, counter-intuitive, or equivocal. Careful design could produce visualizations which convey the general notion of varying levels of error even when the viewer does not have a deep statistical background.

The most common encoding for sample means with associated error is a bar chart with error bars. Despite their ubiquity, many fields (including perceptual psychology, risk analysis, semiotics, and statistics) have suggested severe shortcomings with this encoding, which could result in decisions which are not well-aligned with statistical expectations. While alternate encodings for mean and error have been proposed, to our knowledge none have been rigorously evaluated with respect to these shortcomings.

In this paper we investigate how differences in the presentation of mean and error data result in differing interpretations of viewer confidence and accuracy for judgment tasks. We investigate the drawbacks of the standard encoding for mean and error, bar charts with error bars. We investigate standard practices for depicting mean and errors. We present and evaluate alternative encoding schemes for this data (see Fig. 1). Lastly, we present the results of a crowd-sourced series of experiments that show that bar charts with error bars, the standard approach for visualizing mean and error, do not accurately or consistently convey uncertainty, but that changes in design can promote viewer judgments and viewer certainty that is more in line with statistical expectations, even among a general audience.

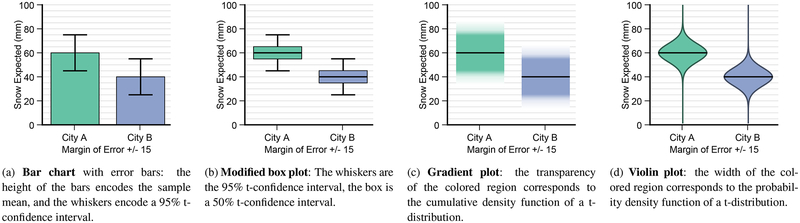
Fig. 1.

Four encodings for mean and error evaluated in this work. Each prioritizes a different aspect of mean and uncertainty, and results in different patterns of judgment and comprehension for tasks requiring statistical inferences.

Contributions: We present a series of issues with how the standard encoding for mean and error, bar charts with error bars, are interpreted by the general audience. We adapt established encodings for distributional data — violin plots[13] and gradient plots[17] — for tasks in inferential statistics. We validate the performance of these encodings with a series of crowd-sourced experiments.

2. Backgrounds

Issues with the presentation of mean and error, especially with bar charts with error bars, have been studied by multiple fields, including psychology, statistics, and visualization. We present a summary of these findings. We provide evidence that, while visualizations of mean and error are valuable, care must be taken in how they are designed and presented, especially to a general audience. We show with an analysis of practices in information visualization and elsewhere that audiences with a wide range of expected statistical backgrounds are nevertheless presented with mean and error data in similar ways. Despite the draw backs we present, we confirm that bar charts with error bars are the modal encoding for presentation of this sort of data in the information visualization community.

2.1. Visualization of Mean and Error

Mean and error, as in confidence intervals or error bars, has been proposed as a solution for some of the perceived deficiencies in traditional significance testing [25], both for pedagogy and in analysis [27]. Unfortunately, while inferential statistics might offer techniques for approaching complex problems, human reasoning (especially in matters of statistics and probability) operates via a series of heuristics that may or may not arrive at the “right” answer. Tversky and Kahneman [32] offer examples of systematic errors these heuristics generate for decision problems based on uncertain data. An example as applied to the information visualization community is the “fallacy of availability” — we remember dramatic or remarkable events with greater ease than ordinary ones, skewing our perception of base rates. For example, a technique which provides good results in most cases but fails catastrophically for a particular case might be seen as more unreliable than a technique that has more frequent, but less severe, failures. Inbar [16] provides evidence that how we visually encode uncertainty and probability can work to “de-bias” data which would ordinarily fall prey to an otherwise inaccurate set of heuristics (by comparison to an outcome maximizing classical statistical view). Designing visualizations to support decision-making and perform de-biasing is not trivial, and how the task is laid out in text can conflict with attempts to de-bias [23]. Even so, the visual presentation of uncertainty can promote better understanding than textual presentation [20].

Error bars, the common way of encoding uncertainty or error, have a number of additional biases, some in concert with other common encodings types. One is ambiguity — an error bar can encode any number of values, from range to standard error. In many cases the error bars are not explicitly labeled, or are labeled in text that is visually distant from the chart in question. This ambiguity, combined with widespread misconceptions about inferential statistics, means that even experts in fields that frequently use error bars have difficulty perceiving how they are connected to statistical significance, estimating p values that are incorrect by orders of magnitude [2]. For error bars with bar charts, the most common combination of mean and error, since bars are large, graphically salient objects that present the visual metaphor of “containing” values, values visually within the bar are perceived as likelier data points than values outside of the bar [24]. Lastly, by presenting error bars as discrete visual objects, designers emphasize an “all or nothing” approach to interpretation—values are either within the bar or they are not. By only showing information about one kind of statistical inference, viewers are unable to draw their own conclusions for their own standards of proof, exacerbating existing problems with null-hypothesis significance testing [6, 18, 28].

2.2. Mean and Error in General Practice

Since mean and error are critical for decision-making based on uncertain data, different communities have codified different approaches to communicating these values, while highlighting the importance of communicating both mean and error to audiences. This is true of both the psychology community, where the audience is assumed to have at least a basic understanding of statistical inference, and also in the journalism and mass communication community, where statistical expertise cannot be assumed.

The American Psychological Association recommends that point estimates “should also, where possible, include confidence intervals” or other error estimates. Furthermore, they should allow the reader to “confirm the basic reported analyses” and also to “construct some effect-size estimates and confidence intervals beyond those supplied”[1]. More recently, the APA has pushed for the greater use and reporting of intervals, as opposed to significance testing [34].

The Associated Press also recommends reporting the margin of error in polling data (in practice, the 95% t-confidence interval) [11]. Since p-values are not common concepts for a general audience, they recommend stating that one candidate is leading if and only if the the lead is greater than twice the margin of error (in practice this is an α value of less than .01). The existence of these guidelines (and the similar reporting and summarization of model and measurement uncertainty in popular, general audience websites such as http://fivethirtyeight.com and http://www.pollster.com), indicates that the display and interpretation of inferential statistics is a problem that extends beyond the academic community.

2.3. Mean and Error in InfoVis

The information visualization community contains members with heterogeneous backgrounds who have different internal statistical practices but nonetheless must report inferential statistics in a mutually intelligible way. We believed that the visualization of mean and error within the community would offer both an example of statistical communication meant for general audiences, as well as provide a diverse set of potential visual designs for communicating statistics. To that end we analyzed the visual display of sample mean and error in the past proceedings of accepted IEEE VisWeek papers in the InfoVis track, 2010–2013. In the 163 papers available, 46 had some visual display of sample means (usually in the context of evaluating the performance of a new visualization tool). Of these 46 papers, 36 (approx. 78%) used error bars to encode some notion of error or spread. The modal encoding was a bar chart with error bars, which occurred in 26 (approx. 56%) of the papers. Boxplots were also common (7 papers, approx. 15%), as were dot plots with error bars (5 papers, approx. 10%).

There was a heterogeneous use of error bars across papers. In many cases the error bars were unlabeled (22 papers, approx. 48%). This is despite the fact that error bars can be used to represent many different quantities. In the papers we found, error bars were labeled as range, 95% confidence intervals, 80% confidence intervals, standard error, standard deviation, or 1.5× the interquartile range (IQR). Should one wish to use these error estimates to estimate statistical significance (a practice which is controversial [28]), each of these interpretations of error would necessitate a different heuristic for “inference by eye” — that is, a different way to determine the relative significance of different effects [9]. Given this ambiguity, a common practice was to denote statistically significant differences with an asterisk; however as the number of sample means increases, the number of glyphs required to explicitly encode all statistical significant pooled sample t-tests increases exponentially. Even if the number of comparisons is small, the link between graphical overlap of confidence intervals and the results of significance testing decays, and the probability of Type I errors increases (cf. techniques such as the Benferroni correction that attempts to correct for the increased likelihood of Type I errors as the number of comparisons increases).

3. Alternatives to Bar Charts with Error Bars

There are many potential designs for mean and uncertainty. Potentially any visual channel can be combined with another encoding to unite a “data map” and an “uncertainty map” [21]. We chose two potential encodings for this data based on current practices for displaying probability distributions, tweaked for the specific use-case of inferential statistics: the gradient plot (which uses α transparency to encode uncertainty), and violin plots (which use width). Neither encoding is particularly common in the information visualization community — only a version of the violin plot, in the form of a vertically-oriented histogram, was found in our search of InfoVis conference papers. We believe this rarity is beneficial for this problem setting, since existing semantic interpretations might interfere with our intended use and meaning of these encodings for this problem (which is similar to, but sufficiently different from the standard visualization problem of visualizing distributions). That is, we do not want viewers to confound visualizations of the distribution of error and the distribution of data.

Processing code for generating all of the plots seen in the paper is available in the supplementary materials.

3.1. Design Goals

The recommendation of style manuals designed for the presentation of results to diverse audiences, combined with the heterogeneity of real world uses of mean and error data, led us to formulate a series of goals for any proposed encoding of mean and error:

• The encoding should clearly present the effect size — that is, accuracy at visualizing error should not come at the expense of clear visualization of the mean.

• The encoding should promote “the right behavior” from viewers (such as refraining from judgment if means are dissimilar but error is very high), even if the viewers lack extensive statistical training. Likewise, viewer confidence in judgments ought to correlate with power of the relevant statistical inferences. These effects should apply to different problem domains and framings.

• The encoding should afford the estimation or comparison of statistical inferences that have not been explicitly supplied.

• The encoding should avoid “all or nothing” binary encodings—the encodings should permit different standards of proof other than (for instance) an α of 0.05. This will likely require encodings which display confidence continuously, rather than as discrete levels.

• The encoding should mitigate known biases in the interpretation of error bars (such as within the bar bias, and mis-estimation of error bars due to the presence of central glyphs). This will likely require encodings which are visually symmetric about the mean.

To fulfill these goals we adapted two existing encodings (usually used for visualizing distributional information), violin plots and gradient plots, for use in inferential tasks. Box plots, as a standard encoding for distributional data, are discussed as a separate case. We believe that these encodings fulfill the design goals presented above. In addition, since they both adapt general techniques for the visualization of distributions, they can be adapted to many different error statistics beyond the t-confidence intervals presented here.

3.2. Gradient Plots

Jackson [17] argues for using color to encode data such as probability distributions functions (pdf). In that technique, and in similar techniques, a sequential color ramp is used to encode likelihood or density, usually varying the α, brightness, or saturation. Low saturation and low α values have a strong semiotic connection with uncertainty [22], and thus are a commonly used visual metaphor for conveying uncertain data [10]. Recent research has shown that using gradients in this manner affords robust understandings of uncertainty even for general audiences [30]. We call this specific technique a “gradient plot.”

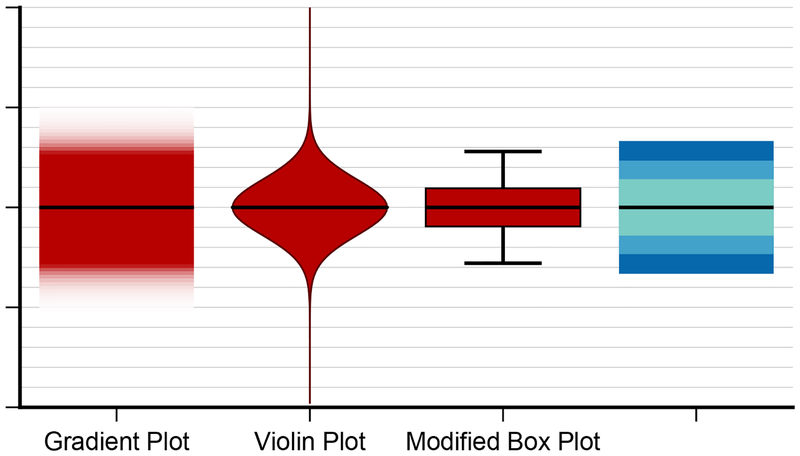
Our version of the gradient plot differs slightly from the standard approach, which is to take the density trace and map each value to a color. We wished to keep some connection with the discreteness of error bars, and so all values within the 95% two-tailed t-confidence interval are fully opaque. Outside of the margin of error, the α value decays with respect to the cumulative probability for the absolute value of the y coordinate based on an underlying t-distribution. That is, the α value of a particular y coordinate is linearly related to the size of the t-confidence interval needed to reach that value — a 95% confidence interval is fully opaque, and the (fictional) 100% confidence interval would be fully transparent. In practice, since the inverse cumulative probability function decays so rapidly, there is a block of solid color surrounded by “fuzzy” edges. Figure 2 shows a sample gradient plot in more detail. Viewers are not very proficient at extracting precise α values, and perhaps can only distinguish only a few different “levels” of transparency [3]. Issues with interpreting α values are exacerbated by the non-standard ways in which tone and transparency are reproduced between displays. Nonetheless, we believe that this imprecision is a “beneficial difficulty” [14] as it discourages artificially precise comparisons where there is a great deal of uncertainty associated with the data. In general we believe the gradient plot is superior to the standard bar chart with error bars for a number of reasons:

Fig. 2.

The alternate plots we propose for encoding mean and error. From left to right gradient plots, violin plots, and modified box plots. The colored bars on the right are standard error, a 95% t-confidence interval, and a 99% confidence interval, for reference.

• A visual metaphor that aligns with expected behavior: minimal transparency (and so uncertainty) within the 95% confidence interval, quickly decaying certainty outside of that region. This extends to comparison: if two samples are very statistically similar than their “fuzzy” regions will overlap.

• Use of a continuous but imprecise visual channel provokes a “willingness to critique” [35] in a way that discrete but precise encodings or styles do not.

• Visual symmetry about the mean, mitigating “within-the-bar” bias (the tendency to see values visually contained by the bar chart as being likelier than values outside the bar).

3.3. Violin Plots

Hintze & Nelson proposed “violin plots” for displaying distributional data [13]. In the canonical implementation a density trace is mirrored about the y axis, and then a box plot is displayed inside the region, forming a smooth, violin-like shape with interior glyphs. “Bean plots” replace the interior box plot with lines representing individual observations [19]. In either case the additional level of detail affords a quick judgment about the general shape of the distribution (cf. a unimodal and a bimodal distribution which might have identical box plots but would have vastly different violin plots). Width and height are both positional encodings of distributional data: position as a visual channel has higher precision than color for viewer estimation tasks. Ibrekk & Granger [15] confirm this inequality for the case of violin plots of probability distributions specifically.

Our version of the violin plot for inferential statistics discards the interior glyphs and encodes the probability density function rather than the sample distribution. We believe that the distribution used to make inferences is more valuable for these tasks than the distribution of the data themselves. Figure 2 shows a sample violin plot of the design used in our study. The pdf is not intrinsically relevant to a significance test, which tends to rely on the cumulative distribution function, or cdf. Initial piloting with the symmetric cdf version of violin plots (where the width of the violin encoded the likelihood that the absolute value of the y position is greater than or equal to the mean) were confusing for the general audience compared to the relatively straightforward pdf violin plots. The general visual metaphor, namely that as we move away from the mean, values become less likely, is maintained even in the pdf version. Additionally, previous work has shown that viewers are capable of aggregating regions of a line graph with some precision[7], affording both cdf- and pdf-reliant judgments. We believe that violin plots used in the way we propose have a number of benefits over standard bar charts with error bars:

• Affordance of comparison of values beyond the discrete “within the margin of error/outside of the margin of error” judgments afforded by bar charts with error bars.

• Use of a strong, high fidelity visual encoding (position) to afford precise readings of the pdf.

• Visual symmetry about the mean, mitigating within-the-bar bias.

3.4. Box Plots

There are several classes of visualizations of distributions which are more common than the two we propose, such as box plots, or dot plots with error bars. While we have included box plots in our evaluation, and they meet many of the design goals above, we believe they are unsuitable for our task. The largest problem is that they are both commonly and popularly used to encode the actual distribution of data. For this problem we do not encode the distribution of data, but (in this case) the distribution of a potential population mean given a sample and certain statistical assumptions. Most commonly used probability distributions (including the Student’s t distribution, the normal distribution, &c.) are unimodal and have infinite extent, while the data about which we are making inferences may not. A box plot as commonly used to depict the distribution of the data is thus several analytical steps removed from a confidence interval. Standard choices in box plots also conflict with our desire to visualize a distribution of population means — whiskers are a form of error bars, but in a box plot whiskers usually denote range or 1.5× the interquartile range (although there are exceptions to this convention, see 2.3). If the first convention is used, then the whiskers of a t-distribution would extend infinitely far along the y-axis. Lastly, there is a perceptual illusion in box plots where large boxes make viewers underestimate the length of error bars, and overestimate the length when boxes are small [29].

Nonetheless, box plots are a popular encoding for distributional data, with many extensions to show a wide variety of higher order statistics [26]. In order to adapt box plots to an inferential rather than descriptive role we made several modifications. The first is that we chose to visualize the pdf of interest rather than the data. The whiskers are the margins of error, in this case the 95% t-confidence interval. We calculate the extent of the box (normally bound by the first and third quartiles of the data) by calculating the inverse cdf at points 0.25 and0.75 (i.e. the locations which are equivalent to 25 and 75% of the of the indefinite integral of the pdf, which is analogous to quartile locations). The center line of the box is the mean. Figure 1 shows an example of a box plot modified in this fashion. We believe that this modification captures the “spirit” of box plots while still being relevant to the task at hand. We believe that even these modified box plots will have the following advantages over bar charts with error bars:

• Additional levels of comparison — while for bars charts with error a y location is either inside the error bar or is not, for box plots there are three such levels (outside the error bar, inside the error bar, inside the box). A point inside the box is within a 50% t-confidence interval from the sample mean.

• Visual symmetry about the mean, mitigating “within-the-bar” bias.

4. Evaluations

The goals of our evaluation were three-fold: to see if general audiences would make decisions that were informed by both mean and error, to assess how certain biases which affect how bar charts with error bars are impacted by our proposed alternate encodings, and to assess other strategies for mitigating these biases. Our results confirmed that our proposed encodings offered concrete benefits over bar charts with error bars. We report on three experiment sets here:

• Our experiment with one-sample judgments presents participants with a single sample mean, postulates a potential outcome (in the form of a red dot), and asks participants to reason about the relationship of this potential outcome to the sample. Our hypothesis was that bar charts are subject to “within-the-bar” bias (where points contained by the bar are seen as likelier than points outside the bar), even for inferential tasks, but that alternate encodings (violin plots and gradient plots) would mitigate this bias.

• Our experiment with textual one-sample judgments evaluates another potential approach to mitigating within-the-bar bias, which is to abstract some of the information from the bar chart itself into text (that does not have the metaphor of visual containment). Our hypothesis was that this approach would be ineffective, and would introduce unacceptable inaccuracy in comparisons.

• Our final experiment with two-sample judgments evaluates our

• alternative encodings in a setting that resembles how these visualizations are frequently used in practice: to compare samples and make predictive inferences about the differences in mean, given the error. Our hypothesis was that viewers with limited statistical backgrounds would be able to make assessments in a way that resembles statistical expectation, but that our alternate encodings would provide a better pattern of performance.

4.1. General Methods

We conducted a series of experiments using Amazon’s Mechanical Turk to evaluate the performance of different graphical encodings for inferential tasks. Participants were recruited solely from the North American Turker population. Participants were exposed to a series of different graphs and asked to complete a set of tasks per graph. Since domain knowledge and presuppositions can alter the visual interpretation of graphs [31], another factor was the framing of the problem: samples were represented as either polling data (“Voter preference for Candidate A”), weather forecast data (“Snowfall predicted in City A”), or financial prediction data (“Payout expected by Fund A”). The experiments were a mixed model design, where the type of encoding seen and the framing problem were both between-subjects factors (each participant saw only one encoding type, and one problem wording), but the distances between means and size of margins of error were within-subjects (participants saw multiple, balanced levels of different sample means and margins of error). In all experiments where we varied the problem framing, it was a significant effect, so it was included as a covariate in our analyses. Including piloting (which includes the results presented in [8], which had a slightly different study design) we recruited 368 total participants. A total of 240 participants were involved in the presented experiments, of which 102 (42.5%) were male, 138 female, (average age = 33.3, σ = 10.2). Of the involved participants, 90 had some college education, 110 were college graduates, and 31 had post-graduate degrees — the remainder were high school graduates with no college experience. Each participant for each experiment saw a total of 36 graphs in sequence. Participants were given no explicit time limit to complete the experimental task, but the median participant took approximately 8 minutes (approx. 14 seconds per graph) to complete the task. We used ColorBrewer [12] to select colors for the stimuli. Figure 3 shows example stimuli and tasks from each of the three experiment sets we present.

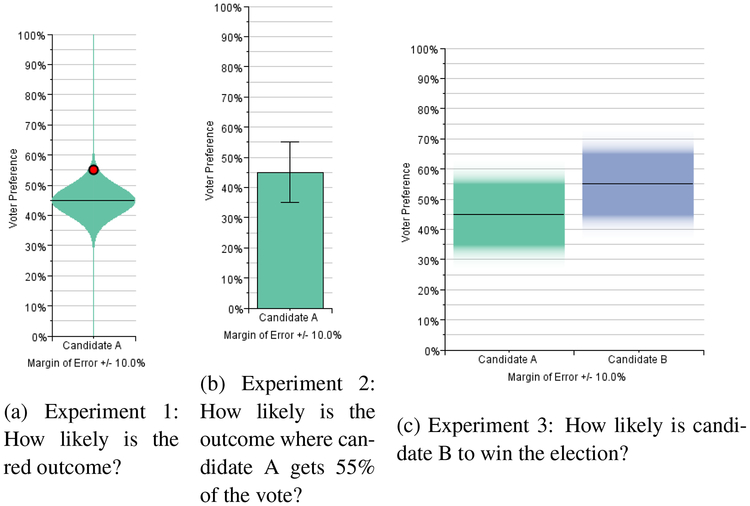
Fig. 3.

Example stimuli from our experiments. Each presents tasks which are similar in concept, but deal with different aspects of the visual presentation of statistical inference. The graphs are presented as violin plots, bar charts with error bars, and gradient plots, respectively, but all experiments tested multiple graph types.

We include data tables, example stimuli, and screenshots of our experimental setup online at http://graphics.cs.wisc.edu/Vis/ErrorBars. F and p-values reported in the results sections are from two-way analyses of covariance (ANCOVAs) unless otherwise stated.

4.2. One-sample judgments

“Within-the-bar” bias as originally proposed is a bias dealing with descriptive statistics: a sample mean is made up of points, points far from the mean are less likely to be members of the sample, but the visual area of a bar in a bar chart creates a region of false certainty. We believed that due to visual metaphor of bar charts, something similar would occur for tasks involving statistical inferences. We believed our alternate encodings, by using a different visual metaphor, would not create this bias.

In this experiment, participants were shown a series of 200×400 pixel graphs, each with one sample value and an associated margin of error. For each graph a red dot was plotted at some set distance from the mean (± 5,10, or 15 units in a 100 unit y-axis). The experimental task dealt only with the interaction between the red dot, the difference from the mean, and the margin of error. Piloting confirmed no significant effect of sample mean on task response, so sample means were randomly selected from the set {35,40,45,50,55,60,65}. There were 6 different levels of margin of error {2.5, 5.0, 7.5,10.0,12.5,15.0}. Each participant saw 36 graphs, 6 per margin of error. There were 3}different levels of the between-subjects encoding factor (violin plot, gradient plot, or bar chart). There were also three levels of problem frame (election, weather, or financial data). The wording of task questions were slightly altered to fit the problem frame. The participants had three main task questions. Verbatim from the election problem frame:

1. How do you think the candidate will perform in the actual election, compared to the red potential outcome? (Fewer votes, more votes)

2. How confident are you about your prediction for question 1, from 1=Least Confident, 7=Most Confident?

3. How likely (or how surprising) do you think the red potential outcome is, given the poll? From 1=Very surprising (not very likely) to 7=Not very surprising (very likely)

The expected behavior (based on statistical expectations) for question 1 is to predict that the sample mean is an accurate estimate of the actual mean (so if the red dot is above the sample mean, you would expect that candidate A would receive fewer votes in the actual election). If this strategy is followed, then question 2 (which is contingent on the guess for question 1) is somewhat analogous to a question about the cumulative density function: what proportion of the probability space is above (or below, depending on the answer to question 1) the red dot? Question 3 by the same reasoning is somewhat analogous to a question about the probability density function. Our hypotheses were:

• H1Participant responses would generally follow expected behavior. That is, participant responses to question 1 would “follow the sample mean” — if the red dot is above the sample, assume the real election will be lower than the red dot, and vice versa. The answers to question 2 should correlate with the cdf of the t distribution given the data, and the answers to question 3 should correlate with the pdf. Both cdf and pdf are modulated by both the difference in value between the predicted outcome and the sample mean, and the margin of error of the sample.
• H2The non-symmetric encoding (bar charts) would exhibit within-the-bar bias — proposed outcomes within the bar would be seen as likelier than outcomes outside of the bar. Symmetric encodings (box, violin, and gradient plots) would not have this bias.
• H3The proposed encodings, which encoded the t-distribution in a non-binary way (gradient and violin plots), would provide more accurate and more confident judgments about the t-distribution than the binary encodings (bar charts and box plots).

4.2.1. Results

We recruited 96 participants, 8 for each combination of problem frame and graph type. We determined significance through two sets of twoway ANCOVAs, testing for the effect of different encodings and data values on confidence in estimating cumulative probability, and estimating the probability density. We included whether the red dot was above or below the mean as a factor as well, and its interaction with the graph type, to explicitly test for “within-the-bar” bias. Inter- and intra- participant variance in performance was included as a covariate, as was problem frame.

Our results generally support H1: We expected participant answers on question 1 to follow the sample mean, and in general this strategy was followed in 87.1% of trials (but see H3 results below).

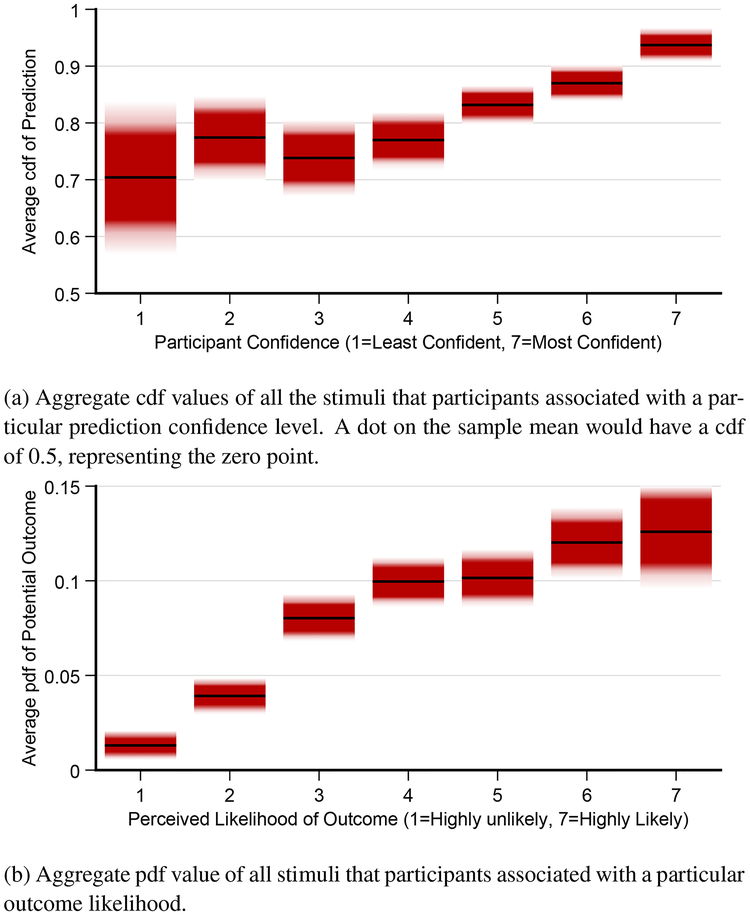
We expected participant answers on question 2 (reported confidence) to follow the cdf. That is, the perceived confidence that the election would have results below a certain proposed result would be correlated with the cdf of the t-distribution, and the perceived confidence that the election would have results higher than a certain value would be 1- the cdf at that location. Indeed, the relevant value (the cdf if the participant predicted the real outcome would be less than the proposed outcome, 1-cdf otherwise) was a significant main effect on reported confidence (F(1,3359) = 55.6, p < 0.0001). Participant’s average reported confidence was positively correlated with the relevant value of the cdf (R² = 0.805, β = 6.78). Figure 4a shows the relationship between answers on question 2 (how confident are you in your prediction?) and the actual cdf values of responses.

Fig. 4.

Gradient plots of our results from the one-sample judgments experiment (§4.2). Participants were shown a sample mean with error, and a red dot representing a proposed outcome. They were asked to predict whether or not the population outcome was likely to be lower or higher than the red dot, and then asked for their confidence in this prediction. This response is analogous to a question about the cdf of the t-distribution (4a). They were also asked how likely the red dot was, given the sample mean. This response is analogous to a question about the pdf of the t-distribution (4b).

We expected participant answers on question 3 (reported likelihood of the proposed outcome) to follow the pdf. That is, the perceived likelihood of a dot plotted on the graph should correlate to the value of the probability distribution at that point. The value of the pdf was only a marginal effect across all results (F(1, 3359)=3.05, p = 0.081), but was a significant effect for trials where the participant followed the correct strategy for question 1 (F(1,3361)=30.2, p < 0.0001). Participant’s average judgments about the likelihood of outcomes was positively correlated with the pdf values of the stimuli presented (R² = 0.842, β = 5.70). Fig 4b shows the relationship between responses on question 3 (“how likely is this proposed outcome?”) and the actual pdf values.

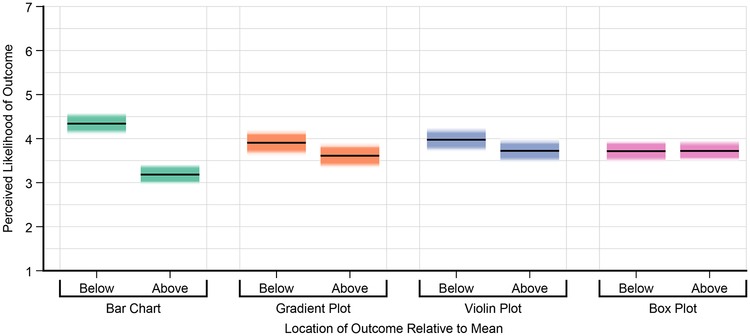
Our results support H2: We observed a significant interaction between the position of the dot (above or below the mean) and encoding (F(2,2)=21.3, p < 0.0001) on the perceived likelihood of the dot as an outcome. A Tukey’s test of Honest Significant Difference (HSD) confirmed that participants in the bar chart condition considered red dots below the mean (and so within the visual area of the bar) significantly more likely than those above the bar. This effect was not significant for any of the remaining, symmetric encodings. Figure 5 summarizes these results.

Fig. 5.

A gradient plot of results from our one-sample judgments experiment (§4.2). Participants were shown a red dot representing a potential outcome and judged how likely this outcome was given the sample mean and the margin of error. Statistical expectation is that likelihood would be symmetric about the mean — that is, red dots above the sample mean would be perceived as just as likely as those below the mean. For bar charts this is not the case — points visually contained by the glyph of the bar (below the sample mean)were seen as likelier than those not contained by the bar. Visually symmetric encodings mitigate this issue.

Our results generally support H3: A Tukey’s HSD confirmed that participants more consistently followed the expected strategy for question 1 (following the sample mean) with symmetric encodings (violin: 89.2% of trials, gradient: 88.5%, box: 87.4%) than with bar charts (83.2%). Graph type was also a significant main effect on confidence (F(3,2982)=7.46, p < 0.0001). A Tukey’s HSD confirmed that participants were significantly more confident with the alternate encoding types which provided more detail about the probability distribution (gradient: M = 5.12, violin: M = 5.06) than with the bar charts and box plots (M = 4.86 for both encodings).

4.2.2. Discussion

This experiment shows that a lay audience, even exposed to encodings that are unfamiliar, and with no expectation of particular training, can perform judgments that are correlated with inferential statistics: points that are far away from the mean are seen as more unlikely, but smaller margins of error also reduce the perceived likelihood of distant points. However, this study shows that within the bar bias (where points contained by the visual boundaries of the bar are seen a likelier members of a sample than those outside it) is present even for inferential tasks, and can be severe enough to not just impact the perceived likelihood of different outcomes, but even the direction of inference. Our proposed encodings, by virtue of being symmetric about the mean, mitigate this bias, for a pattern of judgment that is better aligned with statistical expectations. The alternate encodings also offer more information about the probability distribution than a bar with errors, allowing viewers to reason more confidently at tasks beyond “this value is within the confidence interval” or “this value is beyond the confidence interval.”

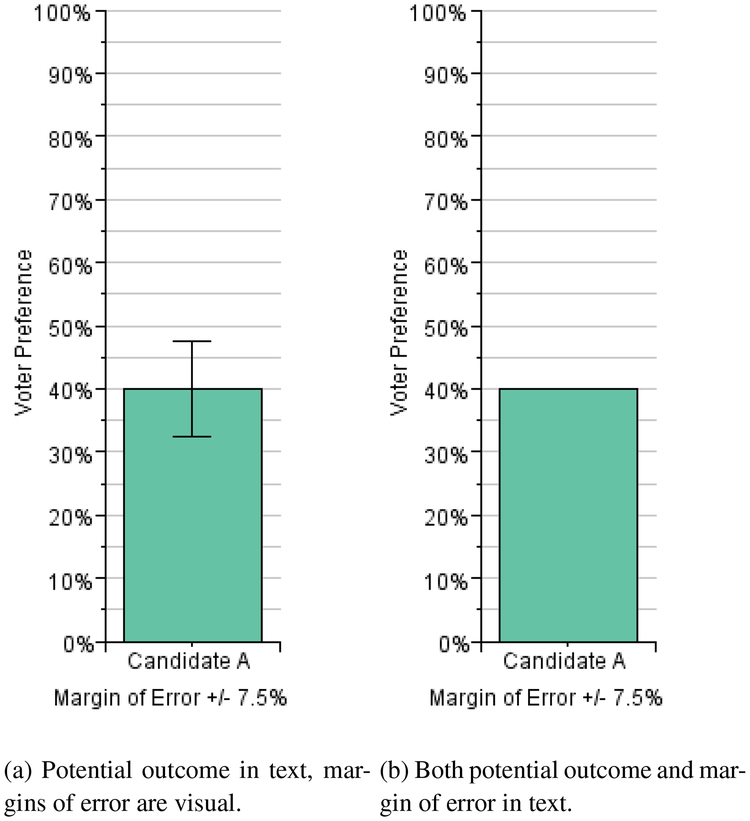
4.3. Textual One-sample judgments

If within-the-bar bias is a visual bias (a red dot is visually contained within a bar), then it is possible that simply encouraging comparisons to be done with only partial assistance of the visualization might mitigate the bias. That is, by moving both the potential outcome and the margins of error to text, judgments might be better aligned with statistical accuracy. This scenario also represents how polling data is frequently depicted in practice, with information about poll size and margin of error written in a legend, but the chart itself displaying the sample means. We wished to evaluate this potential solution, as we speculated that it would introduce a great deal of inaccuracy to judgments and comparisons involving sample means (since it seemed likely that viewers would have to mentally project the text values into the space of the graph).

This experiment had the same factor levels and task questions as the previous experiment (and so each participant saw 36 stimuli), with three differences. The first is that instead of plotting a red dot on the graph itself, the red potential outcome was displayed in colored text under the graph. The second is that we presented only two graph types as a between-subjects factor: a bar chart with error bars, and a bar chart without error bars (in both cases the margin of error was displayed in text below the graph). That is, the conditions reflected moving some portion of the information to text from the graph, either the proposed outcome or both the proposed outcome and the margin of error. This experiment used only one problem frame (the election phrasing).

Our hypotheses were:

• H1Participant responses will be similarly connected with statistical expectation as in the previous experiment — responses to question 1 will align with the direction of the proposed outcome to the sample mean, question 2 will correlate with the cdf, and question 3 with the pdf.
• H2Removing the proposed outcome from the plot and placing it in text will mitigate within the bar bias, since the visual metaphor of containment is broken.

4.3.1. Results

We recruited 48 participants, 24 for each graph type. We conducted similar ANCOVAs as in the previous experiment, testing how different encodings, potential outcome placement, and margin of error affected both cdf and pdf tasks.

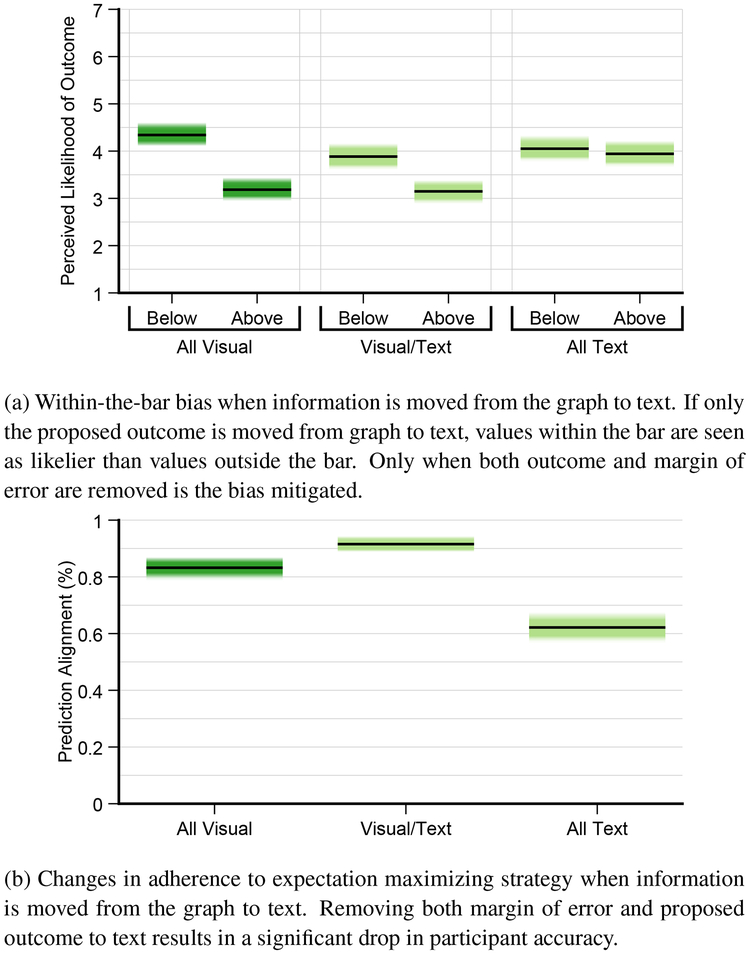
Our results only partially support H1. Our expected strategy for question 1 was that participants would follow the sample mean. A Student’s t-test confirmed that the participants followed the expected strategy significantly more with bar charts with visual error bars (91.6% of trials) than with bar charts with only textual margins of error (62.2%). Figure 7 summarizes this result. Despite this poor performance, participants were significantly more confident in their judgments with the graphs with no visual error bars than in the standard graphs (F(1,1717)=64.8, p < 0.0001, M = 5.4 with no visual error bars, M = 4.9 with visual error bars).

Fig. 7.

Gradient plots of our results of our textual one sample judgments experiment §4.3). When asked to consider potential outcomes, the expected behavior is that viewers will “trust” the sample mean – if a potential outcome is higher than the sample mean, then the “real” outcome will likely by lower than the potential outcome. Participants largely adhered to this strategy throughout experiments. While moving information from the graph to the text does mitigate within the bar bias, it significantly affects alignment with expected strategy. Since viewers must mentally project the potential outcomes and margins of error to the graph space, the relationship between the potential outcome and the sample mean becomes more difficult to analyze.

Our results only partially support H2. There was a significant interaction between the graph type and whether or not the proposed outcome was above or below the mean (F(1,1717)=15.3, p < 0.0001). A post-hoc Tukey’s HSD confirmed that only for graphs with explicit visual error bars was there a significant difference in confidence between values above or below the mean (M = 3.9 and M = 3.1 respectively) – that is, within the bar bias was mitigated by moving both margin of error and proposed outcome to text, but not otherwise.

4.3.2. Discussion

This experiment shows that the visual metaphor of the bar is sufficient to create within the bar bias even if the actual values to be considered are conveyed in text rather than plotted. Removing both margins of error and the proposed value from the graph and to text mitigates this bias, but does so at the expense of making the chart sufficiently confusing to interpret that participants are highly inaccurate (or at least unpredictable) even at simple tasks, and additionally they are unjustifiably more confident in their incorrect judgments.

4.4. Two-sample judgments

In many real world visualizations of mean and error, the primary task is comparison of multiple groups with uncertain values. In order to recommend our alternate encodings for general use, it was important to both confirm that general audiences could generally perform comparison tasks with patterns of uncertainty that were based on statistical expectation.

In this experiment participants were shown 400×400 graphs depicting sample means from two populations (A and B), and asked to make judgments comparing the likely performance of the two. Sample means were normalized such that A+B = 100 units. There were six different sample means for A, {75,60,55,45,40,25}. As with the first experiment, there were six different different margins of error, {2.5,5.0,7.5,10.0,12.5,15.0} (of which the participant saw a total of six per level, for 36 total stimuli), three different between-subjects graph types (bar with error bars, violin plot, or gradient plot), and three between-subjects problem frames (polling, weather, and financial frames). The participants were presented with three main task questions, with wording slightly altered to fit the problem frame (here from the polling frame):

1. If forced to guess, which candidate do you predict will win the actual election?

2. How confident are you about your prediction for question 1, from 1=Least Confident, 7=Most Confident?

3. Which outcome do you think is the most likely in the actual election, from 1=Outcome will be most in favor of A, 7=Outcome will be most in favor of B? (This was measured internally as a value from −3,3, with the “predicted effect size” being the absolute value of the response to this question.)

The expected strategy based on statistical expectation for question 1 is to choose the group with the highest sample mean. Question 2 is then analogous to a two-sample t-test (or, if it is known or assumed that the sample means will always be 100, a one-sample t-test with the null hypothesis that μ=50). Question 3 is then a question about effect size. Since the prediction task was isomorphic to a t-test, we calculated p-values internally for each sample mean comparison. The median p-value was 0.05 by design, however the p-values were not equally distributed among different margins (i.e. where the margins of error were 2.5 or 5.0, there were no stimuli which would fail a t-test at the α = 0.05 level).

Our hypotheses were:

• H1In general, reported confidences and effect sizes will generally follow statistical expectation. That is, participants will “follow the sample” with question 1 — if one candidate is leading in the polls then that candidate will likely lead in the actual election. The participant answers to question 2 should align with p value, and the answers to question 3 ought to align with effect size.
• H2Encodings that encode margin of error in a binary way (bar charts and box plots) will have different patterns of performance than continuous encodings (violin and gradient plots), predicting bigger effects with more (perhaps even unjustified) confidence.

4.4.1. Results

We recruited 96 participants, 8 for each combination of problem frame and graph type. We conducted two sets of one-way ANCOVAs, testing for different encodings, framings, and data values on confidence in predicted “winners,” and predicted effect size. Inter- and intra-participant variance in performance was included as a covariate.

Our results supported H1: We expected answers to question 1 to generally match statistical expectation, which is that the candidate leading in the sample will also lead in the population. This strategy was followed in 95.4% of trials. A Tukey’s HSD showed no signifi-cant difference in strategy adherence among different encodings.

We expected the answers to question 2 to correspond to the p-value of the relevant two sample t-test. Large p-values ought to be associated with low confidence in the predictions of winners in the population based on the sample. Indeed, p-value was a main effect on confidence (F(1,3424)= 49.4, p < 0.0001). Figure 8 shows the connection between reported participant confidence in predictions and actual p-value in detail.

Fig. 8.

Violin plots of the participant’s perceived confidence in their judgment between sample means (i.e. “which of two candidates will win the election, given the polling data?”), plotted against the actual average p-value of the relevant 2-sample t-test. While, for across all presented graph types, participants’ average confidence was negatively correlated with p-value (R² = 0.66, β = 8.30), unlike in statistical practice (where we would reject as not statistically significant differences with p-values of 0.05 or higher), participants in general become gradually more confident on average with decreases in p-value.

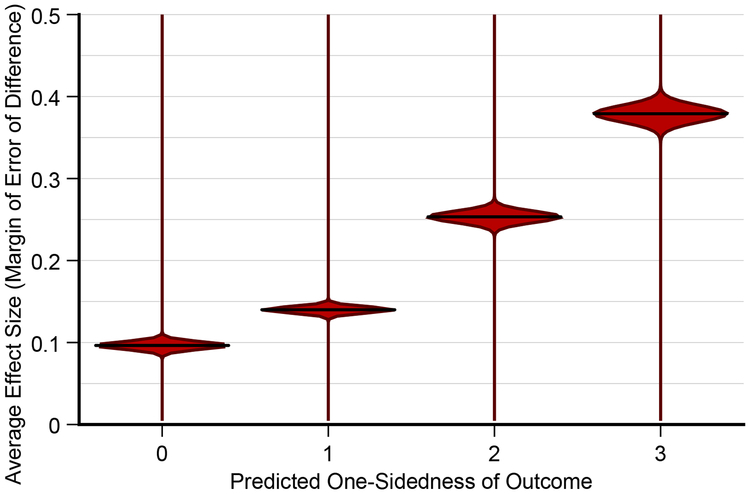
We expected the answers to question 3 to correspond to the effect size. We calculated effect size in terms of number of margins of error between the two sample values (a scalar multiple of Cohen’s d). Effect size was a significant main effect on predicted magnitude of outcome (F(1,3424) = 1210, p < 0.0001). Figure 9 shows this result in detail.

Fig. 9.

A violin plot of results from our two-sample judgments experiment (§4.4). Participants were asked to predict the severity of the outcome based on the sample. For instance, in the election problem frame, they were asked whether the election will be very close or one candidate will win in a landslide. This question is analogous to an estimation of effect size. We display the aggregate effect size (calculated here as the difference between means in terms of the margin of error) for all stimuli that participants associated with a particular level of one-sidedness. Participants’ average estimation of one-sidedness were positively correlated with effect size (R² = 0.567, β = 2.10).

Our results partially supported H2. For the predicted effect size, graph type was a significant main effect (F(3,3424)=23.1, p < 0.0001). A post-hoc Tukey’s HSD confirmed that participants using bar charts predicted outcomes that were significantly larger than with other encodings (bar: M = 1.65, box and gradient: M = 1.54, violin: M = 1.43). This was also the case for confidence in predictions (F(3,3424)=3.38, p = 0.018): participants were significantly more confident in predictions made by bar charts (M = 5.21) than for other encodings, but confidence in the other three charts was not statistically significantly different (gradient: M = 5.07, box and violin: M = 5.02). This gap was even more significant for stimuli which fail to pass a t-test at the0.05 level of significance (M = 4.42 for bar charts vs. M = 4.15 for other encodings). That is, the elevated participant confidence was in a sense unjustified, occurring whether differences were statistically significant or not.

4.4.2. Discussion

Our results show again that the right choice of visualization can allow even a general audience to make decisions that are aligned with statistical expectation, but that these decisions are sensitive to how information is presented. We also show that the alternate encodings, by conveying more detailed information about unlikely outcomes outside of the margin of error, encourage more appropriate doubt about inferences from samples to populations.

5. Summary

Our experiments show that even the general audience is capable of making nuanced statistical inferences from graphical data, taking into account both margin of error and effect size. However, the most common method of visualizing mean and error, bar charts with error bars, have several issues that negatively affect viewer judgments.

Bar charts suffer from:

• Within-the-bar bias: the glyph of a bar provides a false metaphor of containment, where values within the bar are seen as likelier than values outside the bar.

• Binary interpretation: values are within the margins of error, or they are not. This makes it difficult for viewers to confidently make detailed inferences about outcomes, and also makes viewers overestimate effect sizes in comparisons.

We can mitigate these problems by choosing encodings that are visually symmetric and visually continuous. Gradient plots and violin plots are example solutions. Our experiments confirm that these proposed encodings mitigate the biases above, and that modification of bar charts (for instance by moving margins of error to text rather than graphing them explicitly) address these biases only at the expense of introducing inaccuracy and complexity to inferential tasks.

Our experiments show that the general audience can robustly reason about mean and error. However, the issues we described above do occur in practice, and affect how the general audience reasons about uncertain information. The experiments also suggest that these issues can be mitigated with alternate encodings. Moreover, the cost of using alternate encodings appears to be low: even though the ones tested are unfamiliar, they still offer performance advantages to a general audience. The performance improvements of the alternate encodings are measurable in our experiments, but the practical effect of these differences is difficult to determine. Other experimental methodology might better assess the impact on decision making, for example an experiment where stakes are higher might more clearly show differences between encodings. While our experiments show that encodings that follow our design guidelines provide advantages over bar charts with error bars, we have not fully explored the space of designs of mean and error encodings. We believe other designs that fit our guidelines should also have these advantages. Our experiments suggest that some encoding other than bar charts with error bars should be used, but are less specific in recommending the best replacement.

This is not to say that bar charts do not have utility. There are tasks where asymmetric encodings outperform symmetric encodings; for instance, comparing ratios can be done quickly and more accurately with bar charts as compared to dot plots or other encodings where area under the bar is more difficult to estimate [5]. There are also cultural costs involved in adopting non-standard encodings — viewers might prefer to see familiar but known suboptimal encodings.

5.1. Limitations and Future Work

One area not well-covered by our experimental tasks was decision-making: does the presentation of different sorts of statistical graphs result in different actions (beyond mere predictions)? Assessing this facet of inferential behavior would require a more involved series of experiments, with real-world stakes. Likewise, our experiments did not collect a great deal of qualitative data such as viewer preferences for the different chart types: the aesthetics of information visualizations can be an important consideration for how data are perceived and used [33], especially for issues of trust and uncertainty. In the future we hope to modify or extend our set of proposed encodings to cover a wider range of inferential scenarios, including the perception of outlier values, regression, and multi-way comparison, and to deal with additional known biases in human reasoning.

Our data and experimental design also did not reveal many significant differences between our two proposed encodings. Our data do not support the use of one over the other for decisions tasks, however paper authors, reviewers, and colleagues have stated differing preferences between the two on aesthetic and theoretical grounds. We present both in this paper to promote critique, but further work remains to assess both encodings in a principled way.

We also did not investigate how performance might differ with different design decisions. For instance, we colored the gradient chart to make the region within the margin of error fully opaque, but we could have encoded the pdf of the t-distribution directly. We chose a single set of color ramps for our encodings, but it is possible that other choices might bias viewer judgments (for instance, viewers might overestimate the likelihood of outcomes in red violin plots [4]).

5.2. Conclusion

In this paper we illustrate that the most common encoding for displaying sample mean and error — bar charts with error bars — has a number of design flaws which lead to inferences which are not very well correlated with statistical expectation. We show that simple redesigns of these encodings which take into account the semiotics of the visual display of uncertain data can improve viewer performance for a wide range of inferential tasks, even if the viewer has no prior background in statistics. We show that the general audience can achieve good performance on measurable decision tasks with encodings which are less well-known than the standard bar chart.

Fig. 6.

The stimuli for the textual one-sample judgments experiment (§4.3). Unlike in the first experiment, where participants were presented with a red dot representing a potential outcome, here the outcome was presented in text (e.g. “how likely is candidate A to receive 45% of the vote?”). In the second condition the margin of error was also presented textually rather than with explicit error bars.