Ultrafast epithelial contractions provide insights into contraction speed limits and tissue integrity

Significance

We report the fastest epithelial contractility observed to date in the primitive invertebrate Trichoplax adhaerens: Single-cell contraction events reduce cells’ apical area by 50% in one second, at least an order of magnitude faster than other examples. Typically, epithelial contractions enable embryonic systems to change shape during development. Their contractility machinery (actomyosin) is working against high load to achieve dramatic tissue deformation. Here we show that the same machinery can achieve the fast contraction we observe in T. adhaerens, in the lack of load. We also show that unique cell and tissue architecture indeed minimizes the load on a contracting cell. Finally, we suggest a physiological role for these contractions: maintaining the integrity of such a minimalistic tissue.

Abstract

By definition of multicellularity, all animals need to keep their cells attached and intact, despite internal and external forces. Cohesion between epithelial cells provides this key feature. To better understand fundamental limits of this cohesion, we study the epithelium mechanics of an ultrathin (∼25 μm) primitive marine animal Trichoplax adhaerens, composed essentially of two flat epithelial layers. With no known extracellular matrix and no nerves or muscles, T. adhaerens has been claimed to be the “simplest known living animal,” yet is still capable of coordinated locomotion and behavior. Here we report the discovery of the fastest epithelial cellular contractions known in any metazoan, to be found in T. adhaerens dorsal epithelium (50% shrinkage of apical cell area within one second, at least an order of magnitude faster than other known examples). Live imaging reveals emergent contractile patterns that are mostly sporadic single-cell events, but also include propagating contraction waves across the tissue. We show that cell contraction speed can be explained by current models of nonmuscle actin–myosin bundles without load, while the tissue architecture and unique mechanical properties are softening the tissue, minimizing the load on a contracting cell. We propose a hypothesis, in which the physiological role of the contraction dynamics is to resist external stresses while avoiding tissue rupture (“active cohesion”), a concept that can be further applied to engineering of active materials.

Epithelial apical contractions are mostly known to occur during embryonic developmental stages (1–4). These contractions are slow (each contraction lasting minutes to hours) and precisely patterned in both space and time. They play a crucial role in the morphogenesis of the embryo and then desist. The molecular and mechanical mechanism of contraction in these nonmuscle cells, as well as their tissue level control (5–7), are under intensive investigation (5–13). Recently, in vitro spreading assays of adult epithelial monolayers showed similarly slow cellular contractions, though not as canonically patterned (14–18). The triggering and patterning mechanisms of these contractions in somatic tissues are still unknown.

From an evolutionary perspective, cellular contractions have been suggested to play a role in cohesion and coordination in early animals. According to that conjecture, early animal tissues, lacking rigid unifying cell walls, used contractions to counteract ciliary power and achieve coordinated motility (19–21). Ultimately, contractile cells replaced ciliary beating as the dominant mechanism for motility in larger animals. In sponges, a broad class of early divergent animals lacking neurons and muscles, epithelial contractions are used throughout adult life as part of filter feeding, self-cleaning, and defense. These contractions are typically in the form of slow peristaltic waves, though quicker “twitch” responses were reported as well (22–24). In cnidarians, currently considered a later diverging phylum, epithelial contractions are already operated by primitive nerve nets and muscle-like structures (25). The way in which individual cellular contractions coalesce into contractility patterns and ultimately into behavior in primitive animals is largely unknown. Directly studying “simple” basal animals provides new perspectives on epithelial function, as well as insights into the evolutionary leap toward multicellularity.

Here we study the epithelium of an early divergent marine invertebrate, Trichoplax adhaerens as a model “primitive” epithelium. T. adhaerens is one of only a handful of animals that lack nerves and muscles (alongside sponges and some parasites) (26). As such, it is mostly composed of epithelium (>80% cell count) (27). The animal is claimed to be the “simplest” animal known to live today, in metrics like genome length (98 Mbp, ∼11,000 genes), count of cell types (6) and body plan (only dorsal–ventral symmetry breaking) (28, 29). However, despite its biological minimalism, the animal is capable of coordinated behaviors, like directed locomotion and external digestion (30), chemotaxis (31), and propagation by fission (29). The entire organism is essentially a thin flattened sphere (overall ∼25 μm thick, a few millimeters in diameter), made of two epithelial layers connected at their rim (Fig. 1A). In addition, the animal is mostly found crawling on surfaces, keeping an approximately flat shape adherent to the substrate. These geometrical facts allow easy access for imaging and perturbation. The ventral epithelium consists of columnar cells (akin to traditional gut epithelium) and is densely decorated with cilia (30, 32), This ciliary layer beating against the substrate is responsible for the animal’s “gliding” locomotion on the surface. Very much in contrast, the dorsal epithelial cells are composed of extremely thin confluent tiles (only ∼0.5 μm thick) and an overhanging nucleous sac (30, 33) (Fig. 1A). The “T shape” architecture resembles that of sponges’ contractile tissue (exopinacoderm) (34). Only adherens junctions were found in electron microscopy imaging of both epithelia (35) and no extracellular matrix or basement membrane has been observed (26, 29) (further relevant background in SI Appendix, Supplementary Text 1).

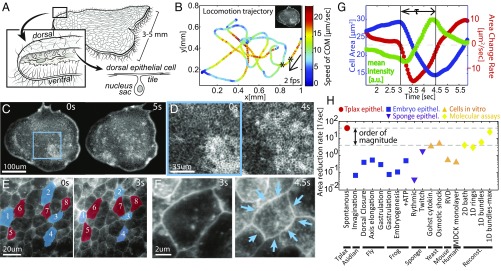
Fig. 1.

Contraction dynamics in T. adhaerens dorsal epithelium (TADE) at all scales. (A) T. adhaerens consists mostly of two flat cell layers of dorsal and ventral epithelia. The dorsal cell tiles are flat with junctions to neighboring cells (SI Appendix, Supplementary Text 1). (B) An example trajectory of an animal’s center of mass, registered while it is freely crawling in 2D and physically tracked for 10 min. The imaging, tracking, and plotting rate is 2 fps. Color represents momentary velocity in the horizontal plane. Inset depicts the relative organism size. The segment between the two asterisks corresponds to the images in C. (C–F) Live imaging of TADE across different length scales, from all cells to a single cell. CMO is used as a live membrane stain. (C and D) Snapshots from a low magnification movie (Movie S4): Cells with smaller sizes are seen brighter due to an increased fluorescent signal. Spatiotemporal patterns are seen in time scales of a few seconds. (E) Snapshots from a high magnification movie (Movie S5): Contraction events are mostly asynchronous, though correlated to neighboring expansions, as the tissue is always kept intact. Cells labeled blue were contracting and those labeled red were expanding in the shown time interval. (F) A single-cell contraction (Movie S5, Top Right). (G) Dynamical measures of the single contraction event in F, after computational segmentation of the cell’s apical area. The overall area reduction in this event is 50% from initial area, and the contraction duration, $\tau$, is 1.5 s. The average pixel intensity increases proportionally to the area reduction. (H) Comparative chart of data from literature reporting epithelium contraction speeds across the animal kingdom and other relevant contraction speeds (citations and comments in SI Appendix, Supplementary Text 2).

In this work we use live, whole animal, cellular imaging and tracking tools to study T. adhaerens dorsal epithelium and explore limits of epithelial contractility and integrity. First, we quantitatively describe the contractility phenomena. Our findings suggest that the tissue behaves as a highly dynamic active solid. We show that the fast contraction speeds observed are feasible within current models of random cytoskeletal bundles without load. We further provide morphological and physiological evidence to show that the tissue is indeed minimizing the load on a contracting cell. In particular, we demonstrate an extreme dynamic range in apical cell size and shape, in response to either external or internal forces, making the tissue surrounding a contraction effectively soft. In the discussion, we propose that an interplay between contractility and softening could provide a means to keep tissue integrity under extensile stress, a mechanism we call “active cohesion.”

Live “in Toto” Imaging Reveals Ultrafast Cellular Contractions

We imaged live animals from the top (dorsal) view, as they crawl freely in two dimensions inside a 30-μm thick microfluidic chamber (Methods). By labeling cell membranes with a fluorescent dye (Cell Mask Orange, CMO), cell borders were visualized in the live animal. To be able to follow the same cells over long durations in a fast-moving animal, we used an automated 2D tracking system (software controlled microscope stage). To improve cell tracking, we further used postprocessing registration algorithms (SIFT, ImageJ) to center the animal and correct for rotations (Methods). Throughout the imaging, animals were crawling on the glass substrate in nontrivial trajectories and speeds of up to 20 μm/s (Fig. 1B). Confinement did not significantly alter locomotion.

Under low magnification, flashes of increased fluorescence were visible in the dorsal epithelium (Fig. 1C and Movie S1). Increasing magnification to see individual cells, while maintaining the whole animal in the field of view (FOV) (in toto imaging), revealed that the fluorescence dynamics are driven by fast cellular contractions (Fig. 1 D–F and Movies S2–S4). Fluorophore density in the apical cell surface increases in correspondence with cell contraction, i.e., the membrane “condenses” in the focal plane. Throughout our data collection, over minutes of imaging, these contraction/expansion dynamics persisted, with no visible ruptures or cellular rearrangements.

Following a single cell during an activity cycle demonstrated the ultrafast kinematics. The cycle included an oversized expansion phase, followed by a fast, concentric contraction of about 50% in cell apical area within roughly 1 s, and finally a slower expansion phase, fully recovering the apical area to baseline (Fig. 1 F and G and Movie S5). Quantitative increase in the fluorescent signal tracks the contraction event reliably (Fig. 1G). A broad comparative literature survey reveals that the contraction speed in T. adhaerens dorsal epithelium is at least an order of magnitude faster than any previously recorded epithelial cell contraction. Only recent in vitro molecular assays of actin–myosin bundles, without any load from cellular infrastructure or constraints, were shown to reach comparable contraction speeds (9) (Fig. 1H and SI Appendix, Supplementary Text 2).

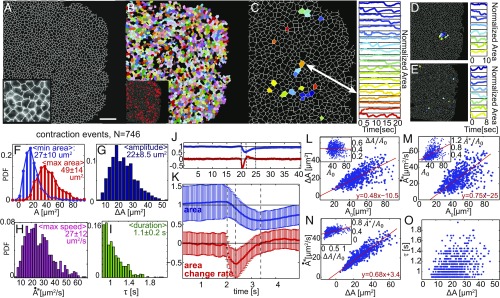
To extract statistical data of the contractility in T. adhaerens dorsal epithelium, we applied computational segmentation and tracking techniques to a movie showing sparse contractions (Methods, Fig. 2 A and B, and Movie S6) and extracted the area of individual cells over time. We arbitrarily defined an active contraction event as a monotonic decrease in cell area that is longer than 0.8 s. Analyzing all cell tracks, we showed that 10–15% of the cells in the monolayer contracted during the 1-min movie (Fig. 2B, Inset). A few examples of the longest trajectories show cells that either contracted once, multiple times, or not at all (Fig. 2C). Statistical distributions of all contractile events show (Fig. 2 F–I and SI Appendix, Fig. 1 A and B) that on average, a contraction reduces 22 μm² (or 45%) of cell area during 1.1 s, while peak speeds reach on average 27 μm²/s (or 85% area per second). In cells that exhibit sequential events, the time delay between subsequent contractions was roughly 5 s (SI Appendix, Fig. 1C). Averaging the time dynamics of all contraction events reinforces the fast and short contractility acceleration phase with a longer and slower deceleration phase, finally followed by a multisecond cell expansion phase (Fig. 2 J and K). We further show that larger cells exhibit higher area reduction (denoted “amplitude,”$\mathrm{\Delta }A$) although the normalized amplitude $\left(\mathrm{\Delta }A/A_0\right)$ is independent of initial cell size. Larger cells also reach higher peak speeds, both in raw and normalized units (${\dot{A}}^{\ast }$ and ${\dot{A}}^{\ast }/A_0$). These correlations serve as benchmarks for our models.

Fig. 2.

Individual contraction statistics. (A) A single frame from a 1-min-long movie of a live animal. Computational segmentation finds roughly 2,000 dorsal epithelial cells in a frame (Movie S6). (Scale bar: 50 μm.) (Inset) Zoom-in shows quality of segmentation on top of the original image. (B) Postsegmentation, individual cells are marked (color) if they have been tracked for more than 2 s. (Inset) Labeled red are all cells that were identified to be contracting sometime during the 1-min movie. (Magnification: A, Inset, 2×; B, Inset is same FOV as B.) (C) Twenty cells that were tracked for the longest durations and their apical area dynamics with time. Color represents cell identity both in the locations map and in the area profiles plot. Area is normalized to be a fraction from maximal area. (D) Eight neighboring cells and their normalized area dynamics. Color represents cell identity. (E) Eight cells that were undergoing contraction at the same time and their following dynamics. (D and E, Left are the same FOV as C.) (F–I) Statistical distributions of the 746 contraction events found in all cell trajectories: initial and final areas ($A$), contraction amplitude ($\mathrm{\Delta }A\hspace{0.17em}=\hspace{0.17em}{A}_{\text{max}}\hspace{0.17em}-\hspace{0.17em}{A}_{\text{min}}$), peak speed (${\dot{A}}^{*}$), and event duration ($\tau$). (J) Aligning all contraction events in time, and normalizing to initial area, we plot the average dynamics of a cell area [$\left(A\left(t\right)/A_0\right)$], in blue and area change rate $\left(A\left(t\right)-A\left(t-1\right)\right)/A\left(t\right)$, in red. (K) Zoomed-in view of J. Error bars are the variance within the different events in a given time point. (L–O) Correlation plots depict that contraction amplitude and speed are positively correlated to initial cell size and to each other, while duration of the contraction event is independent. Each data point shown is a single contraction event.

Spatiotemporal Contraction Patterns Across the Tissue

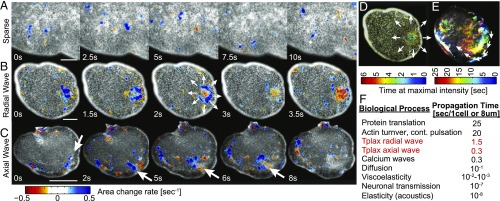
Next, we examined the spatiotemporal contraction patterns in the dorsal epithelium. We used particle image velocimetry (PIV) to estimate the local rate of area change by calculating the divergence of the displacement field (Methods). By eliminating low divergence values, we highlighted the contraction/expansion events (Methods, Fig. 3 A–C, and Movies S2–S4 and S6). Although the repertoire of patterns is vast, a few simple motifs can be identified. Most commonly seen are sparse, sporadic, and asynchronous contractions of individual cells, occurring throughout the tissue (Fig. 3A and Movies S2 and S6). Sometimes all cells in the tissue exhibit active cycles, mostly either in or out of phase from each other (Movie S7). Occasionally traveling waves of contraction are visible, with either radial (Fig. 3 B and D and Movie S3) or uniaxial propagation (Fig. 3 C and E and Movie S4). We manually measured the average wave front propagation in radial waves (0.75 cells per second, n = 4) to be five times slower than that of uniaxial waves (3 cells per second, n = 4). The cellular signal relevant for this cell–cell interaction is faster than actin turnover. However, the wave fronts are slower than diffusion of small molecules in water and similar to calcium wave propagation through a cell membrane (Fig. 3F). We further noticed that wave fronts can both split and/or merge, and propagate either faster or slower than the gliding speed of the organism itself on the substrate (Movie S4), implying the tissue acts as a nonlinear excitable medium.

Fig. 3.

Contractility patterns. (A–C) Examples of common contractile patterns seen in TADE (Movies S2–S4). The raw image is underlying a color representation of the divergence field calculated using PIV. Blue range represents negative divergence (i.e., contraction); red range is positive divergence (expansion). Low values of both contraction and expansion are excluded, for clarity. Since contractions are faster than expansions, red spots are less common. White arrows mark a propagation of a contraction wave. (A) Sparse contractions of mostly individual cells. (Scale bar: 40 μm.) (B) A radially propagating contraction wave that starts at the bulk of the tissue and propagates in all directions. (Scale bar: 100 μm.) (C) A uniaxially propagating contraction wave that initially follows the animal rim and then disperses into the bulk. (Scale bar: 200 μm.) (D and E) The same events as in B and C presented in a color-time technique, similar to maximal intensity projection (Methods). (D and E, Upper show same FOV as B.) (F) Characteristic time scales for different cell–cell signaling mechanisms. Citations and comments are provided in SI Appendix, Supplementary Text 2.

The Measured High Contraction Speeds Are Feasible Within Actin–Myosin Bundle Speed Limits

Actin–myosin networks are known to govern cellular contractions in animal cells and are suspected to do so also in sponges’ pinacocytes (22, 23, 36). We show that F-actin bundles appear as circumferential rings on the apical surface of dorsal cells in fixed, relaxed animals (Methods and SI Appendix, Fig. 2G). This actin ring geometry is similar to other nonmuscle contractile cells and is consistent with previous studies of T. adhaerens morphology (27, 35). We further show that in animals that were not relaxed before fixation, some small cells were located in the center of rosette-like formations, indicating they were frozen in an act of contraction and hence pulling on their neighbors. These cells exhibit high actin density throughout their apical surface (SI Appendix, Fig. 2 H–J).

The high contraction speeds rule out actuation purely by actin filament assembly or turnover (in which relevant time scales are ∼20 s) (37) and suggest actuation by myosin motors activity in a given actin geometry. Interestingly, these quick actuation times may be explained by the recently shown criticality in the transition from bundle stability to contractility (8). The exact identity of the motors is currently unknown. However, homologs of different human myosins (including nonmuscle and skeletal myosin II), as well as key nonmuscle regulatory factors, were found in the T. adhaerens genome using BLAST sequence alignment (SI Appendix, Supplementary Text 3). So far, we were unable to significantly inhibit contractile activity using common actomyosin inhibitory drugs (Blebbistatin, Cytochalasin, Latrinculin, and ML7; see SI Appendix, Supplementary Text 3).

We next performed a calculation to show that current actomyosin contraction models can explain the high contraction speeds we observe. At this point the details of the active machinery, and specifically the speed of the exact motor at play, are still unknown. However, even if we assume the actuator to be the slowest motor known to participate in cellular contractions—nonmuscle (nm)-myosin II (that also has a homologue in T. adhaerens genome)—we demonstrate that the contraction speed is feasible by bundle amplification alone in the lack of counterforce. Using the two known models for bundle contractility—the quasisarcomeric polarization model and the random polarization with buckling model (ref. 38, SI Appendix, Supplementary Text 4a)—we predict a range of speeds that is consistent with our measurements using feasible parameters.

A bundle of initial length $L_0$ that is free in space will shrink with an approximate speed of $\dot{L}=-2V_h{L}_0/D·P\left(K,N\right)$ (Fig. 4 A and B and SI Appendix, Supplementary Text 4), where $V_h$ is the speed of a single motor head (as obtained from common motility assays) and D is the average longitudinal distance between crosslinkers. We introduce $P$ as a contraction probability factor: the percentage of motor filaments that will in fact activate contraction. For a quasisarcomeric geometry, $P=1$. For a randomly polarized actin geometry, we calculate P using combinatorics, assuming a buckling-type model and equal probability for all actin orientation microstates. P in that case is a function of k, the average number of heads in a motor filament that are connected to the bundle, and N, the average number of parallel actin filaments in the bundle (Fig. 4 A–C and SI Appendix, Supplementary Text 4). For this calculation, we allow quick motor attachment–detachment rates, but assume motors are occupying all available sites at all times. Note, that in this view 1D shortening speed is constant in time (assuming “fixed” actin disordered geometry throughout the 1-s contraction). However, that speed is an average over the bundle length, as areas along the bundle are either contracting in full or half speed, or are totally inactive, as reported experimentally (8).

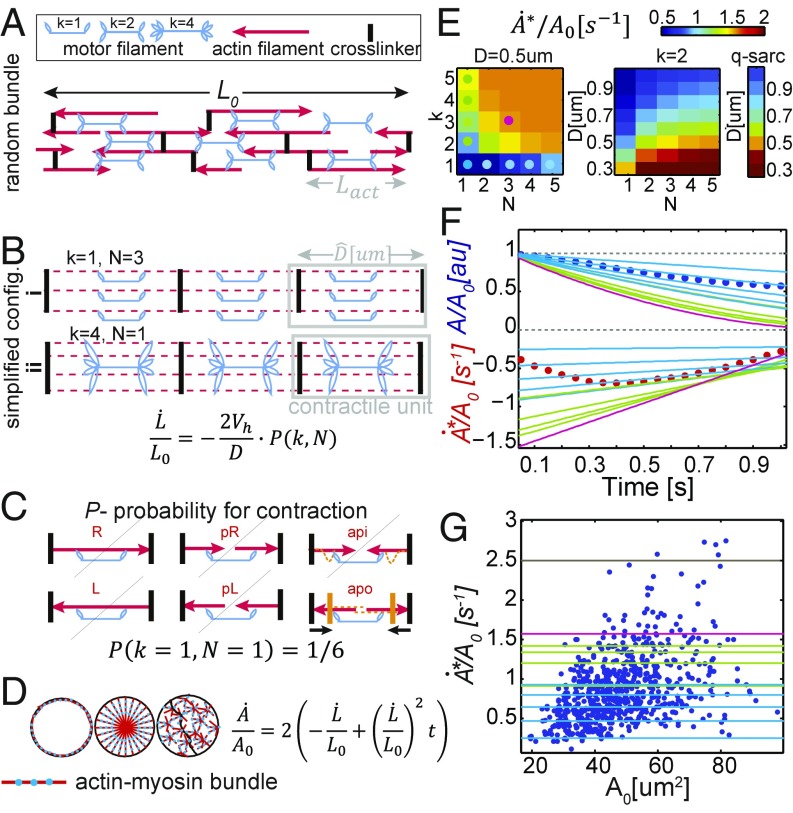
Fig. 4.

TADE ultrafast contraction speed can be explained by nm-myosin II actuation on random actin bundles under minimal load. (A) A randomly polarized actomyosin bundle. Red arrows represent actin filaments. Arrow points at barbed end. (B) Simplified configurations of random bundles, using the bundle-averaged parameters: D, distance between crosslinkers, N, number of actins connected in parallel, and k, number of connected motor head pairs in a single motor filament. Under our assumptions, such bundles will yield constant shrinking speed $\dot{L}$ as in the underlying equation. (C) Visualization of all microstates possible for a motor filament in a random bundle with k = N = 1. The microstates are named after the connected actin polarization: left, right, parallel-left, parallel-right, antiparallel-in, and antiparallel-out. According to the buckling model, only one of these states will yield contraction, hence the probability for this unit to contract (denoted by P) is 1/6 (yellow lines represent the state after motor actuation). (D) Assuming circular cells, all 1D bundle geometries (depicted in dashed red/blue lines) with no load will yield the same area contraction speed $\dot{A}\left(t\right)$ as in the underlying equation. (E) Phase diagrams of the peak area reduction speed (${\dot{A}}^{*}$) as a function of k, N, and D, assuming the buckling model and the quasisarcomeric model. Colored dots represent parameter sets that we use in the following panels. (F and G) Experimental results (circles) compared with our model predictions for nm-myosin II (lines). Line color represents the bundle parameters, as depicted in dots on E. (F) Area and area change rate as a function of time. Circles are the average data from Fig. 2K. Using a very feasible parameter set (magenta), the model predicts higher speeds than our measurements. (G) Normalized peak contraction speed as a function of initial cell area. Circles are data from Fig. 2M, Inset. The black line is the fundamental limit of speed in our model (P = 1, D = length of myosin II motor). The vast majority of the events (n = 741) can be explained by the model in the shown parameter regime.

Applying these 1D contractile speeds to 2D circular cell geometry with circumferential bundles (Fig. 4D), gives the following dynamics in the apical cell area: $\frac{\dot{A}}{A_0}=2\left(\frac{\dot{L}}{L_0}+{\left(\frac{\dot{L}}{L_0}\right)}^{2}t\right)$. This prediction of linear deceleration in cell area with time suggests the following interpretation to the observed contraction phases: The short acceleration phase corresponds to motor recruitment/activation, while the longer deceleration phase means fully developed, constant bundle contraction speed. Area expansion corresponds to relaxation. Note, that in the lack of load, locating bundles in different geometries in the cell would yield the exact same kinematics, due to the linearity between L and L₀ (Fig. 4D).

Taking the literature value for nonmuscle-myosin II sliding speed without load ($V_h=$ 0.2 μm/s) (39, 40), we can estimate numerical values of bundle contractility rates. A high limit for the contraction speed $\dot{A}/A_0$ would be 250% area per second (taking P = 1 and D = L_myo = 0.325 μm, the length of the motor filament). The low speed limit would be 10% area per second (taking a random bundle with k = 1, N = 1, and D = 2L_act+L_myo = 1.325 μm—the minimal serial network that is still percolated). All of our experimental measurements (except very few outliers) are within this predicted range. We further plot a phase diagram for the area contraction speed as a function of k, N, and D in a randomly polarized bundle (Fig. 4E, Left). Interestingly, the nonlinearity of P(k,N) effectively makes P = 1 quite quickly. Hence in the low load regime adding more than a few parallel actins to the bundle, or heads to the motor filament, does not increase the speed significantly (when P reaches 1 the speed values recover the quasisarcomeric model, Fig. 4E, Right). We plot a few of our model predictions on top of our measured data (Fig. 4 F and G). Using k = 3, n = 3 (which are low physiological parameters) and D = L_act = 0.5 μm (as reported in yeast) (41) we get speeds that are higher than the average measured contraction dynamics and exceed 95% of all contraction events observed (Fig. 4 E–G, magenta). Further details are provided in SI Appendix, Supplementary Text 4.

Tissue Architecture and Unique Mechanical Properties Minimize Contraction Load

How is it, then, that the dorsal epithelium of T. adhaerens is the only epithelium found to demonstrate such fast contractions to date? To address this question, we turn our attention to morphological and dynamical features that effectively soften the tissue and hence reduce the mechanical load on the motors performing the work. We specifically examine cell morphology, tissue architecture, membrane features, as well as local and global (spontaneous or induced) variations in cell size and shape.

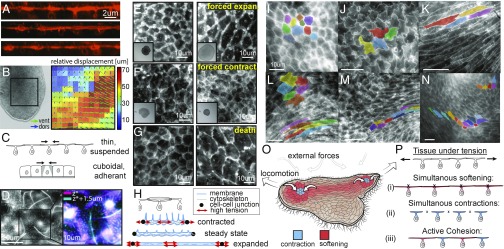
First, we notice that the confluent part of the tissue is extremely thin: 3D confocal imaging shows, in vivo, the unique T shape of the cells, made of ultrathin (<1 μm) cell pavements and overhanging nuclei (Fig. 5A). Second, simultaneous tracking of the dorsal and the ventral epithelia (via a technique of splitting a movie by spatial frequencies, see Methods) reveals relative horizontal sliding of the two epithelial layers against each other. We measure a relative displacement of up to 70 μm (∼10-cell diameters) within 1 s (Fig. 5B and Movie S8). Thus, we deduce at least partial decoupling between the epithelia. Some compliant local connections between the two epithelia may exist, but effectively the dorsal layer is suspended on a liquid cavity and not adherent to the ventral epithelia.

Fig. 5.

TADE unique and active mechanical properties. (A) Live cross-sections (XZ plane) of TADE, reconstructed from confocal Z stacks. Membranes are labeled with CMO. The cells unique T shape is seen, as well as membrane tubes on the apical surface. (B, Left) A snapshot from a movie that shows the animal’s dorsal and ventral epithelia moving independently (Movie S8). (B, Right) Optical plane separation analysis shows relative displacement between epithelia reaching 70 μm (∼10 cells) in 1 s. (C) A sketch comparing a single contraction in a thin, suspended tissue and in a cuboidal, adherent one (see model in SI Appendix, Supplementary Text 5). (D) A top view of live TADE stained with CMO shows membrane tubes. (Right) Zoom-in on a single cell, and stacking of the cell borders plane (magenta) and the excursing tubes plane (cyan). (E–G) TADE capability of extreme variation in cell size: (E) Applying compression in the Z direction on the animal results in 200–350% expansion in dorsal cell size before the first visible tear. (Inset) Whole animal view, FOV: 1.5 mm. (F) Treatment with ionomycin causes immediate contraction of all dorsal cells to ∼50% within a few seconds (Movie S9). (Inset) Whole animal view, FOV: 1.5 mm. (G) An animal left to die in the imaging chamber expanded its dorsal cell area by 400–700%. (H) Our hypothetical free body diagrams of a dorsal cell during contraction, expansion, and steady states. Red arrows mark regions of high tension and potential rupture (either membrane, cytoskeleton, or cell junctions). (I–N) Examples of variable TADE shapes in vivo: polygonal (I), wobbly (J), striated (K), elliptic/amorphic (L, Top Left). These shapes are commonly found in close proximity in space and change rapidly in time (L–N, Movie S10), implying local variability of stiffness. (O) A sketch of the animal from a top view, during locomotion. Color represents our hypothetical view of cells increasing (blue) or decreasing (red) their stiffness, and hence their shape, according to different patterns of external stress. (P) Schematics of possible scenarios in cellular sheets under tension: (i) Cell expansion due to softening may lead to cell rupture. (ii) Simultaneous contractions under the external constraint may lead to junctions’ detachment. (iii) The active cohesion hypothesis suggests active protection against the two rupture modes by asynchronous contractions and expansions, activated according to distinct, local mechanical cues.

We mathematically formulate the effect of these two features on load reduction using a simplified spring model. (Fig. 5C and SI Appendix, Supplementary Text 5): Each cell (of height h) is represented by a parallel stack of horizontal springs of stiffness k at vertical density ${\rho }_{KZ}$. N such “cells” are located laterally to each side of the active cell, and the lateral boundaries are fixed in place. We compare the force required for the central cell to achieve the same apical contraction in a thin and suspended tissue, versus in a cuboidal—cells’ tissue adhered to a substrate (such as in embryos). We assume a constant active force is produced during the contraction in both cases. We find that in both cases, in order to achieve an apical contraction $\mathrm{\Delta }x$, the required force scales linearly with $h\mathrm{\Delta }x$ (SI Appendix, Supplementary Text 5). Using only these two features (cell shape and boundary conditions) we obtain that T. adhaerns dorsal tissue (h = 0.5 μm, diameter = 8 μm) requires a force that is five times lower compared to a Drosophila embryo right before gastrulation (h = diameter = 8 μm). Motivated by this calculation, we performed full 3D finite element calculations (SI Appendix, Fig. S5) for a single contractile cell in a tissue. We compare a thick and a thin tissue architecture, mimicking the two tissue types: Drosophila embryo and T. adhaerens dorsal epithelium, respectively. We find that T. adhaerns dorsal tissue indeed requires lower forces (∼3.5 times) compared to Drosophila embryonic tissue. Next we will show other features that make the two tissues mechanically different; however, these order-of-magnitude calculations show that the T-shape geometry and the unique boundary conditions of the cells alone can reduce the force required to achieve such a fast contraction.

Treating the cells as membrane vesicles filled with fluid, the contraction speed is also limited by the rate of cytoplasm movement and membrane storage. However, the T shape, with the high area-to-volume ratio, suggests that the cells’ fluid content is not a significant factor resisting contraction, as may be in spherical/polyhedral cells. Cellular fluids can either be expelled or translocated within the cell with almost no cost of increased cell pressure. Additionally, we observe a dense collection of membrane tubes protruding from the apical surface of live dorsal epithelial cells (a few dozen tubes per cell, at least 3–4 μm long. See Fig. 5 A and D and SI Appendix, Fig. 2 C and F). These membrane tubes were not seen via actin labeling. We hypothesize that these structures are adaptive membrane storage compartments, enabling fast contractions without membrane loss or synthesis, effectively reducing the resistance to expansion/contraction by the membrane. Similar tubular membrane structures have been observed in in vitro compressed membrane assays (42) in which their creation is immediate, passive, and purely mechanical.

The capability of vital cells to rapidly change their size is another way for this tissue to reduce contraction resistance forces. To show that, we pursued two perturbation experiments: We compressed a live animal in the Z direction, hence applying mostly homogenous, isotropic expansion forces in the XY plane (Methods). In response, the dorsal layer expanded immediately to 200–350% of its original area without tearing or any visible damage (Fig. 5E). In comparison, Madin–Darby canine kidney (MDCK) epithelium cells have been reported to rupture at 170–220% expansion of their original size under quasistatic uniaxial stretch over a few minutes (43). In the second experiment, we exposed the animal to ionomycin (50 μM in artificial sea water), a drug that increases intracellular Ca²⁺. The drug triggers contraction of all cells that reduce their area by 50% within a few seconds (Fig. 5F, SI Appendix, Supplementary Text 3, and Movie S9). In both experiments, visual inspection indicates normal cell size and function are restored after the stress is removed. We conclude, that vital cells can sustain a large range of contracted to expanded states, and quickly move between them. Importantly, under physiological conditions, the cells actively maintain an intermediate size (Fig. 5H). After animal’s death, the confluent cells can expand 400–700% of their steady-state size (Fig. 5G).

Finally, live imaging of locomoting animals under no externally generated stress shows a wide dynamic range in apical shape of the dorsal cells (Fig. 5 I–N and Movie S10). Typically, dorsal cells are either elliptic or amorphic; however, during contraction they become polygonal. Under spontaneous extensile forces (intrinsically driven by the animal’s ventral ciliary layer during locomotion) we notice extremely striated cell shapes. Under spontaneous compression we see wobbly cell edges (shape resembling a jigsaw puzzle) (Movie S10). Remarkably, these diverse shapes are present right next to each other (Fig. 5 L–N). This wide range of shapes infers high, local variability in cortical tension (surface energy), and hence high variability in the effective cells’ stiffness. Cells’ capability to quickly and significantly enlarge/elongate from a base-line size and shape, allows reduction of resistance from neighboring contractions, while keeping the tissue integrity.

Discussion

A contractile epithelial tissue is an active soft matter system with both continuous and discrete characteristics. Cell cortex, cell junctions, and associated cell membrane create a stress-bearing continuum, whereas discrete cells are isolated compartments with finite resources of molecular components, including cytoskeleton filaments, motors, and energy sources. Chemical and mechanical thresholds in cell response enable switching behavior between specific cellular mechanical states. Via changing individual cell states, mechanical properties of the entire tissue can be affected.

A contractile epithelium is modulating not only its local geometry but also its local stiffness: As an individual cell contracts, it increases its resistance to extensile stresses (i.e., increases stiffness) both passively (by cytoskeleton connectivity) and actively (by motor activity). However, T. adhaerens dorsal cells also exhibit dramatic softening, leading to ultralong striated cells (under tension) or buckles (under compression). Softening can result merely from low cytoskeletal connectivity or low motor activity. The capability of cells and tissues to significantly change their stiffness under shear (44–46) or dilation (47, 48) has been previously suggested. Specifically, stress stiffening followed by stress softening under increasing tensile stresses has been shown in actin networks in vitro (49). We hypothesize that physiological values of cell size and stiffness in the T. adhaerens tissue are actively maintained but can be switched (to stiffer or softer modes) in response to chemical or mechanical cues. The mechanism governing this stiffening and softening in T. adhaerens is currently under investigation, and this tissue system provides a unique platform to study the origins of such nonlinearities in lower metazoans.

Keeping tissue integrity is at the heart of epithelium function, especially in the case of primitive epithelium lacking any extra cellular matrix or basement membrane. An animal such as T. adherens, that is primarily an ultrathin cellular sheet, encounters rapid fluctuations of external forces in the open ocean. In addition, the array of cilia on the ventral epithelium applies dynamic forces in different directions, which generates physiologically relevant internal stresses (Movie S10). How does such a seemingly fragile tissue, with minimal intercellular structure, maintain its integrity under these external and internal forces? Its integrity has to be based solely on lateral cohesion to neighboring cells. Under tensile stresses, softening of the cells can prevent detachment of cell–cell junctions, but expose the tissue to rupture by extreme cell strain. On the other hand, cellular contractions solely will prevent such strains on the cells, but risk junction detachment (Fig. 5 P, i and ii).

We hypothesize that T. adhaerens tissue integrity is maintained by activation of the two counteracting cellular phenomena—contraction and softening—both occurring under different mechanical cues. Quick, local switching between these two cellular states allows for a wide range of responses to immediate stress. We suggest it allows the application of overall retraction forces, while ensuring that cell junctions do not reach a critical rupture tension at all times. We coin this type of mechanism active cohesion (Fig. 5 P, iii). The capabilities of this active-elastic material (unlike passive elastic, viscoelastic, or elastoplastic) to cooptimize tissue integrity and resistance to external force are at the focus of our future studies. We also explore how such systems can create spatiotemporal contraction/expansion patterns in the presence of external tensile forces. We speculate that similar principles of active cohesion may apply in epithelia of higher animals, even if operating at different time/length scales.

We propose T. adhaerens as a promising model organism for further study of epithelium biomechanics, for its many conceptual and experimental advantages. As demonstrated in this current work, studying a broader range of animals beyond the classical model systems may bring new perspectives on known biological problems. Our work provides clues for the nature of the putative metazoan ancestor, claimed to be made purely of excitable myoepithlium, the cradle of the creation of nerves and muscles (20, 21, 50). Finally, we believe our work may inspire engineering of intrinsically controlled “smart materials” that actively resist rupture.

Methods

Animal Culture and Sample Preparation.

Cultures of T. adhaerens from the original Grell strain (1971, courtesy of Leo Buss, Yale University, New Haven, CT) were maintained following a published protocol (51). Briefly, organisms were kept in glass Petri dishes filled with artificial seawater (ASW) (Kent reef salt mix in double-distilled water, at 3% salinity) in 19 °C under 18 h of light conditions per day. Plates were initially seeded with red algae type Rhodomonas lens (courtesy of Kevin Uhlinger from Chris Lowe’s laboratory at Hopkins Marine Station, Pacific Grove, CA) and nutrients (Florida aqua farms 1/4,000 volume). One-third of the plate water volume was replaced weekly, maintaining the same nutrient concentration. Live algae were added as needed. Replating may be required after 1–2 mo.

Before any imaging, animals were gently peeled from the plate floor by pipetting and transferred to clean ASW. The shear flows dismissed the debris from the animals’ dorsal surface. Keeping animals in starvation condition for up to 14 h further reduced autofluorescence from dorsal and ventral layers.

The imaging chamber was prepared by placing spacers made by strips of double-sided tape (30 μm thick; Nilto Denko Corporation) on a glass slide (24 mm × 30 mm, no. 1.5). An animal was put in the chamber inside a known volume droplet (typically 20 μL), and let to adhere its ventral side to the slide (5–10 min). Closing with a coverslip (22 mm × 22 mm), the animal was flattened in a known height chamber with a known dorsal–ventral orientation, however free to glide laterally for many millimeters.

Fixation and Related Staining and Imaging.

For fixation, staining, and drug application, we used a technique of liquid replacement by flow in the chamber itself: After closing a chamber with fluid A by placing a coverslip on top, the chamber was still open on two opposite sides by 30-μm-thick cracks. We placed a drop of liquid B on the glass slide next to an “open” side of the chamber and “pulled” liquid A from the opposite side, either by using a piece of tissue (for a fast flow in a thick chamber) or by placing a bigger, hence lower curvature droplet of liquid A on that opposite side (for a slow flow in a thin chamber, using Laplace pressure effect).

Fixation.

Using the liquid replacement technique, samples were fixed by flowing Lavdowsky solution (50% ethanol, 10% formaldehyde, 1% acetic acid, 0.1% Tween 20) (52) on top of ice, left at −20 °C overnight, and then washed in PBS three times for 15 min each.

For SEM imaging.

After fixation, the liquid was replaced by a mix of ethanol in PBS in increasing concentrations: 50%, 70%, 90%, 100%, 15 min each. Finally, the liquid was replaced by hexamethyldisilazane in ethanol (50%, 100%, 15 min each). We peeled the top coverslip and allowed it to dry in a vacuum desiccator overnight. Samples were then coated with ∼10 nm gold (Denton Desk II sputter coater). Imaging was performed in a variable-pressure scanning electron microscope (Hitachi S-3400N).

For F-actin staining.

Before fixation, some samples were relaxed by introducing 0.3 M sucrose in ASW for 10 min (27). After fixation and washing, samples were permeabilized using PBST (PBS+ 0.1% Tween 20, three washes of 15 min each), blocked in 1% BSA in PBST for 1 h, stained with Phalloidin (Alexa-Fluor 647, Cell Signaling Technology, 1:40 in PBST) for 3 h and washed with PBST (three times, 15 min each). Images were taken with a Zeiss LSM 780 confocal microscope.

Live Imaging.

For live fluorescent imaging of cell membranes, we added to the chamber CMO 1:500 in ASW (Thermo Fisher). We imaged the dorsal surface using a TE2000-U microscope (Nikon), with lambda XL (Sutter Instruments) light source and an Orca 4.0 scientific CMOS camera (Hamamatsu). Using a 40× oil objective, we achieved in toto imaging of ∼2,000 cells in an animal allowing a single-cell resolution. Oil objectives 60× and 100× were used as well for higher magnification. Typical movies were taken at 20 fps.

Confocal Imaging with Physical Tracking and Z Stacks.

For physical tracking of the organism over longer periods of time, we used the Nikon TiE inverted microscope with Andor Neo sCMOS camera, NIS-Elements software, and Nikon HCS JOBS software patch. The JOBS software patch enables stage control and custom real-time tracking. We used a 2D cross-correlation method to keep the organism in the field of view at all times. Tracking movies were typically taken at 3 fps, for a duration of 10 min.

We used this optical setting to track an animal at the cell tiles plane, but also to take Z stacks that were later reconstructed and presented as XZ cross-section (ImageJ).

Computational Registration, Cell Segmentation, and Tracking.

Acquired movies of 20 fps were taken to ImageJ, to enhance contrast and eliminate translations and rotations computationally (SIFT algorithm). Frangi filter algorithm was applied on each frame (Matlab2014), to find lines in the image using the Hessian operator. Finally, an iterative water-shedding algorithm was used to further segment large areas at their narrowest point (Matlab2014).

After segmentation was complete on all frames, we labeled and tracked individual cells in time by finding minimal cell center displacement (Matlab2014). We allowed cells to “disappear” for a few frames while keeping their identity, but we kept only tracks that were longer than 2 measured seconds.

Area data in time was measured directly. The normalized amplitude of a contraction event was taken to be $\text{A}\left(\text{final}\right)-\text{A}\left(\text{initial}\right)/\text{A}\left(\text{initial}\right)$. The normalized peak speed was calculated as $(\text{A}\left(\text{t}\right)-\text{A}\left(\text{t}-\text{dt}\right))/\left(\text{A}\left(\text{t}\right)\text{dt}\right).$ Data were smoothed by a total variation regularization algorithm.

PIV and the Color-Time Technique.

Movies underwent PIV (matpiv, Matlab 2014), using an interrogation window of 25 μm (32 pixels), and time interval of 0.3 s. The divergence of the displacement fields is shown, eliminating low absolute values (under 15% per second). The algorithm uses different objects as “tracers,” from cell walls to subcellular puncta on the membrane.

In parallel, the same movies were processed in a color-time technique, to show time progression in a single image: each frame’s gray levels were translated to intensity levels of a specific color, representing the time point it was taken at. We show the normalized sum of all colored frames. Pixels with distinct color have changed during the movie and had maximal intensity at the time represented by the color (similar to “maximal intensity projection” representation). Pixels that did not change intensity during the movie, appear in gray level. We present the color map on top of the first frame of the movie.

Spatial Frequency Split.

A movie was taken with bright field illumination (Nikon Multizoom AZ100) at 20 fps. The animal’s dorsal layer in that setting was mostly transparent; however, some small features and speckles on it were seen very sharply as they were in midfocal plane. The ventral layer was seen dark in the background. We separated the data from the two optical planes by their spatial frequency (highpass >6% and lowpass <1% of the Fourier transform dimensions). Performing PIV on each of the resulting movies separately, and taking the difference between the displacement fields, gave the relative displacements between the layers.

Tissue Z Compression.

While a live animal was visualized, we applied gentle compression forces in the Z direction, either by dropping a flat weight of 35 grams on the animal in an open Petri dish (constant stress setting, Fig. 5E, low magnification images), or by placing a coverslip on top of the animal that was in a controlled volume droplet, to create a controlled thickness chamber (constant strain setting, Fig. 5E, high magnification images). Removing the weight in the first case, or adding ASW to the chamber, allowed the animal to recover completely and go back to normal cell size.