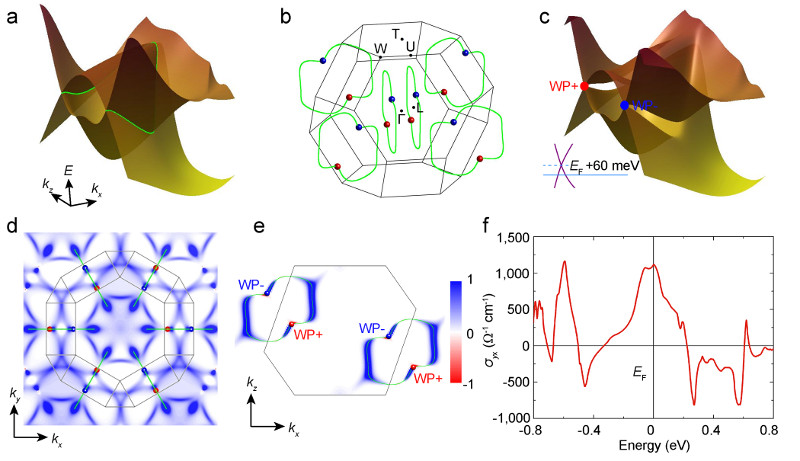
Figure 2. Theoretical calculations of the Berry curvature and anomalous Hall conductivity.

a, Linear band crossings form a nodal ring in the mirror plane. b, The nodal rings and distribution of the Weyl points in the Brillouin zone. c, Spin-orbit coupling breaks the nodal ring band structure into opened gaps and Weyl nodes. The Weyl nodes are located just 60 meV above the Fermi level, and the gapped nodal lines are distributed around the Fermi level. d, Berry curvature distribution projected to the k_x–k_y plane. e, Berry curvature distribution in the k_y = 0 plane. The color bar for d and e are in arbitrary units. f, Energy dependence of the anomalous Hall conductivity in terms of the components of ${\Omega }_{yx}^z(k).$