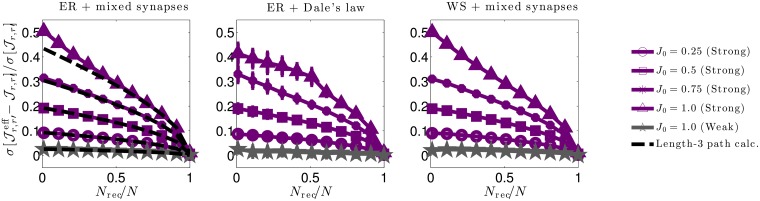
Fig 5. Relative changes in interaction strength due to hidden neurons for three network types.

We quantify relative changes in interaction strength between effective (${\mathcal{J}}_{r,r^{\prime }}^{\text{eff}}$) and true (${\mathcal{J}}_{r,r^{\prime }}$) interactions by the (sample) root-square-mean deviation, $\sigma [{\mathcal{J}}_{r,r^{\prime }}^{\text{eff}}-{\mathcal{J}}_{r,r^{\prime }}]$, normalized by the true synaptic weight (sample) standard deviation $\sigma \left[{\mathcal{J}}_{r,r^{\prime }}\right]$. We do so for three (sparse) network types: Left. An Erdős-Réyni (ER) network with “mixed synapses” (i.e., Dale’s law not imposed) with normally distributed synaptic weights. Middle. An ER network with Dale’s law imposed, (i.e., each neuron’s outgoing synaptic weights all have the same sign). Right. A Watts-Strogatz (WS) small world network with 30% rewired connections and mixed synapses. All network types yield qualitatively similar results. In each plot solid lines are numerical estimates of the sample standard deviation of the difference between effective coupling weights ${\mathcal{J}}_{r,r^{\prime }}^{\text{eff}}$ and true coupling weights ${\mathcal{J}}_{r,r^{\prime }}$ between neurons r ≠ r′, normalized by the standard deviation of ${\mathcal{J}}_{r,r^{\prime }}$. These estimates account for all paths through hidden neurons. Purple lines correspond to synaptic weights with standard deviation $J_0/\sqrt{pN}$ (strong coupling), while grey lines correspond to synaptic weights with standard deviation J₀/pN (weak coupling). For weak 1/N coupling (grey), the ratio of standard deviations is $\mathcal{O}(1/\sqrt{N})$. For strong $1/\sqrt{N}$ coupling (purple) the ratio is $\mathcal{O}\left(1\right)$ and grows in strength as the fraction of recorded neurons N_rec/N decreases or the typical synaptic strength J₀ increases. The dashed black lines in the left plot show theoretical estimates accounting only for hidden paths of length-3 connecting recorded neurons (Eq (4). Deviations from the length-3 prediction at small f and large J₀ indicate that contributions from circuit paths involving many hidden neurons are significant in these regimes.