Abstract
The behavior of a nanoparticle in solution depends strongly on the particle’s physical and chemical characteristics, most notably the particle size and the surface properties. Accurately characterizing these properties is critical for quality control in a wide variety of industries. To understand a complex and polydisperse nanoparticle suspension, however, ensemble averaging is not sufficient, and there is a great need for direct measurements of size and surface properties at the individual nanoparticle level. In this work, we present an analysis technique for simultaneous characterization of particle-surface interactions and size using near-field light scattering and verify it using Brownian-dynamics simulations. Using a nanophotonic waveguide, single particles can be stably held near the waveguide’s surface by strongly localized optical forces. By tracking the dynamic 3D motion of the particle under the influence of these forces using an optical microscope, it is possible to extract the particle-surface interaction forces, as well as to estimate the size and refractive index of the nanoparticle. Because of the strong light-scattering signal, this method is viable for high-throughput characterization of particles as small as 100 nm in only a few seconds each.
I. INTRODUCTION
Nanoparticles have attracted significant interest in recent years due to a host of unique electronic, optical, and chemical properties [1–6]. These properties are governed largely by surface effects and are highly dependent on the particles’ size and surface area [7–10]. In many applications, the diameter of the particles used can have a dramatic effect on the particle’s functionality: for instance, whether the particles effectively screen out UV radiation [11], exhibit dangerous cytotoxicity in the body [7], or reliably pass through cell walls to enable targeted therapeutics [12]. It is critical, therefore, to determine the nanoparticle size distribution to ensure the safety and effectiveness of these engineered suspensions. This determination is especially difficult for heterogeneous suspensions, where traditional sizing methods such as dynamic light scattering will average out a lot of the inherent polydispersity and can lead to misleading conclusions [13].
To address this problem, a number of new experimental techniques have developed that focus on building up size distributions by measuring individual nanoparticles rather than a population-averaged value [13]. These techniques, including single-particle tracking [14], have been used successfully to size a variety of metallic, dielectric, and biological nanoparticles [4,15–18].
While single-particle size analysis is essential for understanding nanoparticle behavior, it does not tell the complete story. The interactions between nanoparticles and interfaces, for example, are highly dependent on the particles’ surface properties, which can be difficult to predict from first principles [8,12,19]. There are techniques which have been developed to directly measure the interactions of particles with surfaces, including a technique we have developed called nanophotonic force microscopy (NFM) [20,21]. This method offers very-high-resolution information on particle-surface-interaction forces, but no information on the size of each particle.
For many applications, one would expect coupling between a particle’s size and surface properties, for instance, when evaluating the long-term stability of a particle with an engineered surface coating [12]. In these situations, it would be highly desirable to have a technique capable of measuring both the size and the surface properties of the same individual nanoparticle simultaneously. In this work, we develop a new single-particle-tracking technique which is compatible with our previous nanophotonic force microscopy technique for force spectroscopy.
Single-particle-tracking analysis (SPT) relies on scattered light from particles which are freely diffusing in the bulk solution. This reliance allows for particle sizing, but not for probing the forces on the particles in the solution. Conversely, in NFM, the particles are held close to the surface by optical forces to allow for surface-interaction measurements, and the particles are not freely diffusing. Using analytic theory and Brownian-dynamics simulations, we show that it is still possible to extract the radius of a trapped nanoparticle by analyzing the particle’s 3D motion on very short time scales with a high-speed camera. We also demonstrate how the applied optical forces can be used to differentiate particles of the same size by their refractive index. Using simulations, we show that reasonable sizing accuracies (<10% error) can be achieved with a low-cost industrial camera and with as little as 1 s of video data per particle. This method is fully compatible with our previous NFM technique, and both analyses can be run on the same video.
A. Single-particle-tracking analysis
Prior to introducing our new methodology, we will review the method of diffusive sizing by SPT. SPT is an optical-analysis technique which works by tracking the Brownian motion of individual nanoparticles using light scattering [13]. Briefly, a laser is focused into a flow cell containing the nanoparticle suspension using a glass prism. The laser light scatters off the nanoparticles in the solution, and the scattered light from each particle is collected above the flow cell onto a CCD detector. The position of each particle in each frame can be determined with subpixel resolution using a particle-localization algorithm. The motion of the particle can then be tracked frame by frame as the particle undergoes Brownian motion in order to find the mean-squared displacement [14]. For free (2D) diffusion, the mean-squared displacement is linearly proportional to the particle’s hydrodynamic-diffusion coefficient, D, by
| (1) |
where Δt is the elapsed time since the start of tracking. Using the Stokes-Einstein relation [22], this diffusion coefficient can be related to the particle’s radius:
| (2) |
B. Nanophotonic force microscopy
The NFM technique works by pulling nanoparticles towards a waveguide surface using an attractive optical-gradient force [20,21]. The attractive optical-gradient force is counterbalanced by surface forces (such as repulsive electrostatic forces, hydrophobic interactions, and steric hindrances), and the particle undergoes confined Brownian motion around a stable equilibrium height. Within the evanescent field of the waveguide, the optical intensity decays exponentially with height. As the particle fluctuates in height, it will scatter less light when farther from the surface and more light when nearer to the surface. Since the decay constant of the light intensity is known, the changes in intensity can be transformed into changes in height. If the light scattered by the particle is recorded over time, an equilibrium distribution of the heights can be found, and the potential well of the particle-surface interaction can be calculated using Boltzmann statistics. After the optical-gradient component to the potential well is subtracted, a force-distance curve resulting from the surface force alone can be found. A schematic overview of this experimental procedure is shown in Figs. 1(a) and 1(b). Readers interested in further details are referred to our previous publications [20,21].
FIG. 1.

Overview of the 3D nanophotonic force microscopy (3D NFM) technique. (a) Free-body diagram of the optical and nonoptical forces which act on the nanoparticle captured in the evanescent field of a 1D nanophotonic waveguide. As the particle moves within the exponentially decaying field, it scatters light which is detected by an industrial CMOS camera from above. The inset coordinate system is used for the rest of this work. (b) In the z direction (perpendicular to the waveguide surface), the particle fluctuates in a potential well created by attractive optical and repulsive surface forces. The magnitude of the surface forces can be found by tracking the height-dependent scattering intensity over time, finding the combined potential well, and subtracting the optical contribution. (c) Along the y direction, the particle fluctuates stochastically in a harmonic potential due to confined Brownian motion. The x-y position of the particle is found by localizing the centroid of the light-scattering pattern, and the y position is tracked over time. The motion over short time intervals is used to extract a diffusion coefficient and, eventually, the particle size.
II. 3D NFM THEORY
Here, we describe a hybrid technique which combines NFM with a modified single-particle sizing method that accounts for the applied optical forces and surface effects. For this method, a nanoparticle is trapped within the evanescent field of the optical waveguide [Fig. 1(a)]. The particle’s position is then tracked in 3D-space motion along the z axis by integrating the scattered intensity (as in NFM), and motion in the x-y plane is determined by subpixel localization (as in SPT). The z motion can be used to find the force-distance curve, and the x-y motion can be used to find the particle size using a modified single-particle-tracking analysis. This x-y motion is more complicated than the free-diffusion case owing to two major factors: (1) the influence of optical forces on the diffusive motion and (2) an anisotropic hindering of the diffusion coefficient near the surface. If these two effects can be accounted for, however, it is possible to use these complications to determine not only the particle size but also the refractive index. We will address the modifications necessary for both of these effects now.
A. Diffusion with optical forces
To combine the two measurement techniques, we must first consider the functional form of the optical forces resulting from the optical waveguide. A Rayleigh particle in the nonuniform evanescent field will experience four distinct forces: (a) an optical-scattering force, proportional to the intensity of the light field and the particle’s dielectric constant, (b) an optical-absorption force that results from momentum transfer by absorbing the incident light, (c) an attractive optical-gradient force proportional to the gradient in intensity, and (d) a size- and height-dependent hydrodynamic-drag force [23]. The magnitude of these forces is given by
| (3a) |
| (3b) |
| (3c) |
| (3d) |
where I0 is the optical intensity at the particle’s position and α is the optical polarizability, given by
| (4) |
where εp and εm are the permittivities of the particle and the medium, respectively [23].
A diagram of the relevant optical forces along all three dimensions, as well as the coordinate system used for the rest of the discussion, is shown in Fig. 1(a). Although the optical-force field is three dimensional, it is useful to consider the projections along dimension separately for the sake of clarity.
Along the x direction, the particle is propelled at terminal velocity by the balance of the optical-scattering force and the Stokes-drag force [24]. This motion is not used for sizing the particle, but it does rapidly push particles in a line through the field of view of the camera.
The optical gradient force along the z direction can be used to balance the repulsive surface forces, exactly the same as in 1D NFM. The histogram of sampled heights can then be used to find the force-distance curve of the particle-surface interaction [Fig. 1(b)].
In additional to the downward optical-gradient force used for the NFM measurement, however, there is also a component of the optical-gradient force in plane which points towards the center of the waveguide. Along the y axis, this gradient force acts as a harmonic optical restoring force which is counterbalanced by Brownian fluctuations. The probability density function of the nanoparticle position over time is governed by the Smoluchowski equation for a harmonic biasing force [25]:
| (5) |
where D is the diffusion coefficient and ktrap is the spring constant of the effective harmonic potential.
Following the results of Lindner et al. for tethered Brownian motion [25], the solution to this partial differential equation is a Gaussian function with a variance that grows over time and depends on both ktrap and D:
| (6) |
Both ktrap and D will vary with the size of the particle. ktrap also depends on additional parameters, such as the optical intensity and the refractive index of the nanoparticle material. Since these parameters are not always known a priori, it is desirable for sizing to decouple these effects and find only the diffusion coefficient. This result can be accomplished by observing the particle motion for very short time lags where the particle has not yet been significantly influenced by the restoring force. Taking a first-order Taylor approximation of Eq. (6), we find that
| (7) |
for short time lags. In this limit, the variance of the displacement is linearly proportional to the lag between measurements. With a sufficiently fast frame rate, therefore, it is possible to determine an effective diffusion coefficient by fitting a line through the first three frame lags and finding the slope [Fig. 1(c)].
B. Brownian-dynamics simulations
In a conventional single-particle-tracking analysis, the particle undergoes free Brownian motion in two dimensions [22]. Under these conditions, the accuracy of the reconstruction does not depend on the position sampling rate and an accurate diffusion coefficient can be found by tracking a single particle for relatively long times at a relatively low frame rate [e.g., recording for 60 s with a 30 frames/s CCD detector] [15]. As seen in Eq. (6), however, there is an explicit time dependence when the particle is held within the evanescent field. If the sampling rate is too low, the observed dynamics will be a combination of motion due to diffusion and motion due to the optical restoring force, which would be difficult to decouple. As a result, our modified 3D NFM technique must operate at significantly higher frame rates than the traditional configuration allows.
To evaluate the viability of SPT for nanoparticle sizing with optical forces, we perform a series of 1D Brownian-dynamics simulations at a sampling rate of 5000 frames/s. This frame rate is achievable with many industrial CMOS cameras, which is critical for a low-cost, high-throughput analysis method [26].
A representative Brownian-dynamics simulation of an R = 150 nm particle is shown in Fig. 2. Figure 2(a) shows a 1-s-generated Brownian trajectory of motion within the harmonic potential along the y axis, sampled at 5000 frames/s. Starting with each frame, the displacement of the particle after n = 1, 2, 3 frames is calculated. These displacements are normally distributed, and the variance of that distribution can be plotted as a function of time lag, as suggested by Eq. (6). As seen in Figs. 2(b) and 2(c), the chosen sampling rate of 5000 frames/s is fast enough that the variance grows linearly in time, corresponding to the diffusive regime. A line is then fit to the first three points of the variance curve, the slope of which is twice the effective diffusion coefficient.
FIG. 2.

Brownian-dynamics simulation demonstrating the hydrodynamic-diffusion-analysis technique. (a) The 1D Brownian trajectory of a nanoparticle with radius 150 nm in the harmonic potential 20 nm above the optical waveguide. To approximate a reasonable experimental implementation, the particle is sampled at 5000 frames/s for one second. (b) The variance of the particle motion as a function of time lags between frames. In the short-time-lag limit, the motion can be approximated as purely diffusive and the variance is linear in time. (c) A linear fit to the first three time lags (i.e., the displacement after one frame, two frames, and three frames) to determine an effective diffusion coefficient.
For this representative particle, we extract a diffusion coefficient of 0.69 μm2/s from a ground-truth value of 0.73 μm2/s for a 5.5% deviation. This error could be reduced by increasing the frame rate further or taking data for a longer interval, but 5000 frames/s for 1 s gives a conservative estimate of what is possible in a realistic experiment. Note that if the frame lag is too long (e.g., even 5–10 ms), a linear fit to the remaining data in Fig. 2(b) will greatly underestimate the diffusion coefficient and the analysis technique will not be reliable.
C. Diffusion near the surface
Because of the close proximity of the nanoparticle to the waveguide surface, the inverse relationship between R and D predicted by the Stokes-Einstein relation does not hold [27–29]. Instead, it is well known that the diffusion coefficient very near a wall is hindered by hydrodynamic effects, and the effective diffusion coefficient of the particle is both anisotropic and height dependent. Along the y direction, this hindered diffusion coefficient is given by Faxen’s law:
| (8) |
| (9) |
where z is the height of the bottom of the particle above the surface, R is the radius of the particle, and Dbulk is the ordinary Stokes-Einstein diffusion coefficient far from the wall [27]. This function is plotted as a function of height for three particle sizes in Fig. 3(a).
FIG. 3.

Particle size estimation incorporating hindered diffusion theory. (a) The hindered diffusion coefficient for nanoparticles of a given size above the surface, according to Faxen’s law. The degree of hindering depends on both the size of the particle and the height above the surface. (b) If the height above the surface is known, the particle radius can be uniquely determined from the measured diffusion coefficient. (c) Measured diffusion coefficients for N = 100 simulated particles at each size using the short-time-lag diffusion method outlined in Fig. 2. The equilibrium height is 20 nm above the waveguide surface. (d) The error in the measured radius for particles which are considered to be on the surface but are actually at a height h above the surface. As the height above the surface increases to 20 nm, the radius is systematically underestimated, but by less than 50 nm. N = 10 particles per size. Error bars represent one standard deviation. h = 0 is defined as direct contact between the waveguide surface and the bottom of the nanoparticle.
This relationship has been verified experimentally using a variety of measurement techniques [27–29]. In general, the hindered diffusion coefficient is a nonlinear function of the height of the particle above the waveguide surface, as well as the particle’s radius. For a particle of an unknown radius at an unknown height, therefore, it is not possible to uniquely determine the size directly from the diffusion coefficient. If the distance from the bottom of the particle to the waveguide is known, however, this expression can replace the Stokes-Einstein diffusion coefficient to relate the effective diffusion coefficient directly to the particle’s radius, achieving the same simplicity as the free-diffusion analysis used in SPT.
Figure 3(b) shows the diffusion coefficient as a function of size, as predicted by Faxen’s law. For a given height (defined as the distance between the bottom of the particle and the waveguide surface), the measured diffusion coefficient is sufficient for extracting the particle radius. If the height is completely unknown, however, there is not a one-to-one relationship; a 50-nm particle at the surface, for example, will diffuse similarly to a 150-nm one that is 100 nm away. In Fig. 3(c), Brownian-dynamics simulations are performed to confirm that nanoparticles with radii from 50 to 300 nm are distinguishable from their measured diffusion coefficients. For each size, 100 particles are simulated for 1 s each using the predicted diffusion coefficient at a fixed height of 20 nm, and the diffusion coefficients are extracted using the method outlined in Fig. 2. As seen from the simulation results, the stochastic nature of the Brownian-dynamics simulations adds some uncertainty to the measured diffusion coefficient; nevertheless, 1 s of data at 5000 frames/s is sufficient to recover the input diffusion coefficients and separate the particles by radius.
D. Manipulating the particle height
In the previous analysis, it was shown that the particle size can be determined from the measured diffusion coefficient as long as the height above the surface is known. While variations in height are relatively easy to determine, absolute height is more difficult to discern. Although the amount of light scattered by the particle varies exponentially with height, the absolute height above the surface cannot be calculated without knowing the optical intensity at the waveguide surface. In total-internal-reflection microscopy, determining the optical intensity is often accomplished by increasing the salt concentration irreversibly by sticking the particles to the surface at the end of an experiment [28]. This action is not compatible with high-throughput analysis, as it would contaminate the surface of the chip and prevent further particles from being analyzed.
For our waveguide-based light-scattering technique, however, the equilibrium height above the surface is not fixed but depends on the balance of optical and surface forces. The magnitude of the optical force can be tuned by varying the input optical power in the waveguide. By increasing the input power sufficiently, a nanoparticle in the evanescent field of the waveguide can be driven into contact or near contact with the waveguide surface. In the regime where h/R → 0, the hindered diffusion coefficient parallel to the waveguide converges towards a common value of 0.324 for all values of R. Incorporating Eq. (9) yields a simple inverse relationship between the measured diffusion coefficient from the linear fit and the particle’s radius,
| (10) |
For an appropriately tuned optical power, it is possible to estimate the size of each particle and to measure the particle-surface-interaction potential very close to the wall. The systematic error in the calculated radius will depend on how close the nanoparticle can be brought to the wall without sticking irreversibly. Figure 3(d) shows a size analysis of simulated particles of different nominal sizes. For each size, the approximation that the particle is very close to the surface is used, and the actual height above the surface is increased to test the error in the final value as a result of that assumption. As the height above the surface increases, the size of the particle is systematically underestimated, but it remains within 50 nm of the nominal radius for a gap height of 20 nm. The effect of this systematic bias is most significant for the smallest particles, but it can be diminished by increasing the optical power to shift the equilibrium height closer to the surface.
E. Refining the size estimate
For applications where only coarse binning by size is needed, the approximation in Eq. (10) may be sufficient. For higher precision, however, additional techniques may be employed. From the exponential decay of the evanescent field, we know that the ratio of the scattered intensity at any two points can be used to find the distance between them:
| (11) |
The small but measurable changes in height around an equilibrium position zeq form the basis of the NFM force-spectroscopy technique [21]. If the optical power is cycled into the waveguide periodically, however, the particle will jump between multiple equilibrium positions, zeq,1, zeq,2,…, zeq,n. Because of hindered diffusion, the effective diffusion coefficient for the particle at each height will depend nonlinearly on the height and the particle size. By sequentially recording the motion of a single particle around N equilibrium positions, therefore, it is possible to derive a nonlinear system of equations,
| (12) |
| (13) |
The difference between the equilibrium heights Δzij can be found from the ratio of the power-normalized intensities by
| (14) |
where Pi is the optical input power for the ith equilibrium height. Although this system of equations does not have a generalized analytic solution, the radius and the heights can still be found numerically with a nonlinear optimization scheme to improve the accuracy of the initial guess for an R based on the coarser model. Ideally, many heights could be used to maximize the fitting accuracy, but the accuracy of both the diffusion and the force information at each height decreases when the observation time is too low. Using the waveguide architecture from our previous work, we find that particles are observable for an average of 3–5 s each and require 3000 frames to produce accurate statistics [20]. Coupled with the sampling rate of 5000 frames/s, this result allows for at least five powers to be sampled with the minimum 3000 frames at each height. Figures 4(a) and 4(b) show the results of a simulation where single 150- and 300-nm particles are sampled at five different heights for 1 s each, respectively. For the 300-nm particle, the closest gap distance between the particle and the surface is set to 25 nm. A minimum gap height of 29 nm and a measured radius of 317 nm are obtained from a nonlinear least-squares fit to the five effective diffusion coefficients for a 5% error at the estimated size. If the camera frame rate were higher, more powers could be sampled that meet the 3000-frame threshold, and the accuracy of this size estimation could be further improved. NFM analysis of the multiple-power data would also yield a separate potential well centered around each height. The resulting potential wells could then be stitched together to give a fuller picture of the surface forces up to 150 nm above the waveguide surface.
FIG. 4.
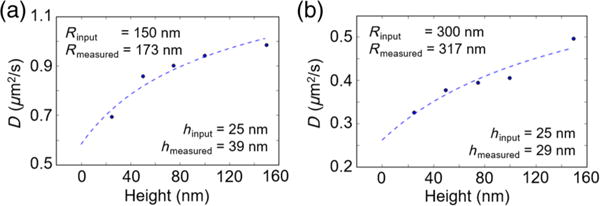
Refining the particle size estimate. Representative simulation of (a) an R = 150 nm particle and (b) an R = 300 nm particle measured at five different heights for 1 s each. Using the measured diffusion coefficients and the relative displacements between the heights, the radius and the absolute height are estimated through a nonlinear least-squares fit. The relative error in the size estimate decreases for larger particles, as the hindered diffusion coefficient is less sensitive to small fluctuations in height.
F. Optical and material characterization
Using the diffusive-analysis technique from the previous section, it is possible to determine the hydrodynamic size of individual nanoparticles because the dynamics of the particle at sufficiently short time lags do not depend on the magnitude of the optical forces. For unknown samples, the optical properties of the particles, e.g., the refractive index, do not need to be known a priori in order to determine the size. Nevertheless, the optical properties of the particles are often critically important and can, for instance, help to differentiate subpopulations which are similar in size but composed of different materials. Taking Eq. (6) and looking only during the long time limit, we find that the variance depends only on the trap stiffness:
| (15) |
matching the predictions of the equipartition theorem. This trap stiffness can then be compared with the analytic expression for the optical-gradient force along the y axis:
| (16) |
where α is the optical polarizability of the particle, as defined in Eq. (4). The polarizability of a single nanoparticle can then be found either by calculating the prefactor in Eq. (16) or by normalization between multiple particles [30]:
| (17) |
Since R can be found through the nonoptical diffusive characterization from the previous section, a direct comparison of the refractive indices of the particles is possible. This comparison is especially useful for distinguishing metallic and dielectric nanoparticles of similar sizes, as the difference in optical polarizability can be several orders of magnitude [31].
Figure 5 shows a representative simulation which demonstrates the decoupling of size and optical properties for particles with two different polarizabilities. For this demonstration, two particles are simulated at the same height, one with a polarizability α and one with a polarizability 4α. Figure 5(a) shows the histogram of particle positions in the long time limit after the particle has reached equilibrium due to the optical-gradient forces. In this regime, the measured variance in the particle position is inversely proportional to the polarizability and independent of the diffusion coefficient, as predicted by Eq. (17). In Fig. 5(b), the same two simulated particles are analyzed for only the short time lags, as in Fig. 2. In this limit, the extracted diffusion coefficients are comparable despite the stark difference in polarizability. By analyzing the same raw particle trajectory in the two regimes, it is possible to independently measure both ktrap and D. For a hetero geneous sample, this analysis can be used to distinguish subpopulations of particles that are similar in size, but not in refractive index. This method could be useful in screening out unwanted contaminants in the solution, such as dust particles or oil droplets, which could otherwise affect the size-distribution accuracy.
FIG. 5.

Separation of particles with different optical polarizabilities. (a) Determination of the trap stiffness through longtime equilibrium data for two simulated particles sampled at 5000 frames/s for 1 s. The optical-trap stiffness (proportional to the variance) is 4 times larger for the red particle than the blue one. (b) Hydrodynamic sizing analysis for the same two particles using short-time-lag diffusion. Although the difference in polarizability is clear from the longtime data, the short-time diffusion is independent of the magnitude of the optical force and the measured diffusion (and the radius) is similar for both particles.
III. EXPERIMENTAL VERIFICATION
To demonstrate that the proposed sizing method is indeed viable for high-throughput industrial use, we perform an experiment using a low-cost industrial CMOS camera (acA2000-165um, Basler AG) and a commercially available optofluidic waveguide chip (Optofluidics, Inc.). For this experiment, we optically trap an R = 150 nm National Institute of Standards and Technology (NIST) traceable polystyrene bead over the surface of an optical waveguide and record the scattered-light intensity using a 20× objective on an optical microscope at 3000 frames/s. The radius of 150 nm is selected to match as closely as possible the simulations in Fig. 2. The position of the trapped particle is then tracked in two dimensions using the MOSAIC ParticleTracker plug-in for ImageJ [32].
Figure 6(a) shows a still image of the light scattered by the particle during the experiment. The red circle shows the position of the particle as determined by the spot-tracking algorithm. Figure 6(b) shows the trajectory of the particle over 3 s (or, equivalently, 9000 frames). The motion of the particle along the two tracked dimensions agrees well with the predictions of both the analytic theory and the Brownian-dynamics simulations. Along the x direction, the particle is pushed at a terminal velocity by the balance of the optical scattering force [Eq. (3a)] and the Stokes drag [Eq. (3d)], as expected. Along the y direction, the particle fluctuates around the center of the waveguide, consistent with the Brownian-dynamics trajectory generated in Fig. 2(a). The variance of the displacement is then calculated as a function of the time lag between frames and a linear fit is performed to the first three frame lags (Δt = 1/3000, 2/3000, 3/3000). Using Eq. (7), we can then calculate an effective diffusion coefficient of 0.52 μm2/s [Fig. 6(c)].
FIG. 6.

Dynamic analysis of a trapped R = 150 nm polystyrene bead. (a) A still image of the scattered-light signal from the trapped particle. The red circle shows the particle location determined by the spot-tracking algorithm. (b) The 2D trajectory of the particle, captured at 3000 frames/s for 3 s. The x and y axes are as defined in Fig. 1. (c) The variance of the particle motion along the y axis as a function of the time lag, averaged over the full 3-s trajectory. The effective diffusion coefficient is calculated from a linear fit to the first three points, following the analysis of the simulations in Fig. 2.
If we assume that the optical power is sufficiently high that the particle is just above the waveguide surface, we can now apply the result of Eq. (10) to estimate the particle size. For this experiment, this approximation works very well and a more refined estimate is not necessary; a measured diffusion coefficient of 0.52 μm2/s corresponds to a particle with a radius of 151 nm, a less than 1% deviation from the value of 150 nm quoted by NIST.
For this particle, a full 3 s of data is used to determine the size. The Brownian diffusion along the y direction is inherently stochastic; as such, there will always be variation in the measured diffusion coefficient, and this variation will depend strongly on the number of frames captured. It is worth investigating, therefore, how well the analysis technique works for shorter trajectories. In Fig. 7, we calculate the effective diffusion and radius of the particle for subsets of the full 3-s video to see the influence of the video length on the final accuracy. For very short trajectories, we see a significant overestimation of the diffusion coefficient (or, equivalently, an underestimation of the radius). After 1 s of data, however, the measured radius is within 10% of the nominal value. For a coarser estimate of size, therefore, it may be possible to characterize a particle in just 1 s, or 3000 frames of video data. In our previous work, we demonstrated that 3000 frames of data are also sufficient to obtain accurate interaction-force measurements, meaning that simultaneous measurements of force and size could be achievable in 1 s with reasonable accuracy. In practice, most dielectric particles remain within the field of view for 3–5 s, allowing for better convergence and more accurate results [20]. For a concentrated particle solution under ideal conditions, this amount of viewing time allows for the potential single-particle analysis of approximately 1000 particles per hour.
FIG. 7.
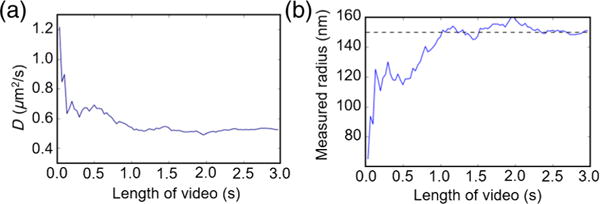
Convergence of the measured radius over time. (a) The diffusion coefficient is determined by analyzing a subsection of the tracked particle trajectory to determine the length of time required for an accurate value. For short trajectories, the diffusion coefficient is significantly overestimated, but it rapidly approaches a final constant value for tracks longer than 1 s. (b) The radius calculated from the measured diffusion coefficient using Eq. (10). The measured radius shows very good agreement with the nominal radius quoted by the manufacturer (R = 150 nm; shown with the dotted line) for times greater than 1 s.
For the experimental data here, we consider only the accuracy of measuring a single particle. For very polydisperse samples, however, the reality is slightly more complicated. As discussed previously, the optical-gradient force is size dependent (R3); at a given optical power, larger particles will be held more easily than smaller ones. This consequence would, in general, lead to a bias in the measured particle distribution, where large particles are overrepresented and small particles are underrepresented.
In the absence of surface forces, this bias can be quantified straightforwardly; a 400-nm particle, for instance, experiences an attractive optical force which is roughly 70% that of a 450-nm particle. The bias is more complicated near the waveguide surface, however, because both the optical-gradient forces and the repulsive surface forces increase as the height above the surface decreases. At a higher optical power, both larger and smaller particles can be stably held, but they will be held at different equilibrium heights. In a high-salt environment with a Debye length of 20 nm, for example, a 7-nm difference in equilibrium height is enough to compensate for the same 30% decrease in optical-force strength. Since this effect depends on the magnitude and height dependence of the surface forces (which are unknown a priori), the effect cannot be easily estimated from first principles. Because there is simultaneous analysis along multiple axes, however, it should be possible to combine force and size data after an experiment to estimate the degree of bias in the measurement and make appropriate corrections. It would also be possible to directly measure particles at different heights using the multiple-power analysis shown in Fig. 4. We hope to investigate this effect in the future by performing experiments with known polydisperse samples, but doing so here is outside the scope of the current work.
While techniques exist for measuring both the size and the particle-surface-interaction potentials of nanoscale particles, there are no existing techniques which can do both simultaneously at high throughput. In this work, we describe an extension to our previous force-spectroscopy method which uses the dynamics of a particle within an evanescent field to probe its size, forces, and optical properties. Using a combination of analytic theory and Brownian-dynamics simulations, we outline the procedure for applying this technique and investigate the particle sizing accuracy for single-particle trajectories. We also demonstrate the viability of the analysis technique using experimental data gathered under practically realizable conditions, finding very good agreement with the simulated results with only 3 s of video data. We believe that this technique could be used to process hundreds of particles per hour using a commercial CMOS camera, making it especially viable for rapid quality control of nanoparticle suspensions.
Acknowledgments
This work is supported by the U.S. National Institutes of Health under Grant No. 1R01GM106420-01. The authors would like to thank Dr. Christopher Earhart from Optofluidics, Inc., for the valuable discussions and the relevant experimental parameters for the numerical simulations.
Footnotes
The author declare the following competing financial interest: D. E. has an equity interest in Optofluidics, Inc., a company commercializing technologies related to this work.
References
- 1.Binshan Ju, Tailiang Fan, Mingxue Ma. Enhanced oil recovery by flooding with hydrophilic nanoparticles. China Particuol. 2006;4:41. [Google Scholar]
- 2.ShamsiJazeyi Hadi, Miller Clarence A, Wong Michael S, James M. Tour, and Rafael Verduzco, Polymer coated nanoparticles for enhanced oil recovery. J Appl Polym Sci. 2014;131:40576. [Google Scholar]
- 3.Kokura Satoshi, Handa Osamu, Takagi Tomohisa, Ishikawa Takeshi, Naito Yuji, Yoshikawa Toshikazu. Silver nanoparticles as a safe preservative for use in cosmetics. Nanomed Nanotechnol Biol Med. 2010;6:570. doi: 10.1016/j.nano.2009.12.002. [DOI] [PubMed] [Google Scholar]
- 4.Gallego-Urrea Julian A, Tuoriniemi Jani, Hassellv Martin. Applications of particle-tracking analysis to the determination of size distributions and concentrations of nanoparticles in environmental, biological and food samples, TrAC. Trends Anal Chem. 2011;30:473. [Google Scholar]
- 5.Echegoyen Yolanda, Nerin Cristina. Nanoparticle release from nano-silver antimicrobial food containers. Food Chem Toxicol. 2013;62:16. doi: 10.1016/j.fct.2013.08.014. [DOI] [PubMed] [Google Scholar]
- 6.Cushen M, Kerry J, Morris M, Cruz-Romero M, Cummins E. Nanotechnologies in the food industry— Recent developments, risks and regulation. Trends Food Sci Technol. 2012;24:30. [Google Scholar]
- 7.Park Margriet VDZ, Neigh Arianne M, Vermeulen Jolanda P, de la Fonteyne Liset JJ, Verharen Henny W, Bried Jacob J, van Loveren Henk, de Jong Wim H. The effect of particle size on the cytotoxicity, inflammation, developmental toxicity and genotoxicity of silver nanoparticles. Biomaterials. 2011;32:9810. doi: 10.1016/j.biomaterials.2011.08.085. [DOI] [PubMed] [Google Scholar]
- 8.Walkey Carl D, Olsen Jonathan B, Guo Hongbo, Emili Andrew, Chan Warren CW. Nanoparticle size and surface chemistry determine serum protein adsorption and macrophage uptake. J Am Chem Soc. 2012;134:2139. doi: 10.1021/ja2084338. [DOI] [PubMed] [Google Scholar]
- 9.Lundqvist Martin, Stigler Johannes, Elia Giuliano, Lynch Iseult, Cedervall Tommy, Dawson Kenneth A. Nanoparticle size and surface properties determine the protein corona with possible implications for biological impacts. Proc Natl Acad Sci U S A. 2008;105:14265. doi: 10.1073/pnas.0805135105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tenzer Stefan, Docter Dominic, Rosfa Susanne, Wlodarski Alexandra, Kuharev Jörg, Rekik Alexander, Knauer Shirley K, Bantz Christoph, Nawroth Thomas, Bier Carolin, Sirirattanapan Jarinratn, Mann Wolf, Treuel Lennart, Zellner Reinhard, Maskos Michael, Schild Hansjörg, Stauber Roland H. Nanoparticle size is a critical physico-chemical determinant of the human blood plasma corona: A comprehensive quantitative proteomic analysis. ACS Nano. 2011;5:7155. doi: 10.1021/nn201950e. [DOI] [PubMed] [Google Scholar]
- 11.Wissing SA, Mller RH. Solid lipid nanoparticles as carrier for sunscreens: In vitro release and in vivo skin penetration. J Control Release. 2002;81:225. doi: 10.1016/s0168-3659(02)00056-1. [DOI] [PubMed] [Google Scholar]
- 12.Win Khin Yin, Feng Si-Shen. Effects of particle size and surface coating on cellular uptake of polymeric nanoparticles for oral delivery of anticancer drugs. Biomaterials. 2005;26:2713. doi: 10.1016/j.biomaterials.2004.07.050. [DOI] [PubMed] [Google Scholar]
- 13.Filipe Vasco, Hawe Andrea, Jiskoot Wim. Critical evaluation of nanoparticle tracking analysis (NTA) by nanosight for the measurement of nanoparticles and protein aggregates. Pharm Res. 2010;27:796. doi: 10.1007/s11095-010-0073-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Malloy A, Carr B. Nanoparticle tracking analysis—The Halo™ system. Part Syst Charact. 2006;23:197. [Google Scholar]
- 15.Dragovic Rebecca A, Gardiner Christopher, Brooks Alexandra S, Tannetta Dionne S, Ferguson David JP, Hole Patrick, Carr Bob, Redman Christopher WG, Harris Adrian L, Dobson Peter J. Sizing and phenotyping of cellular vesicles using nanoparticle tracking analysis. Nanomed Nanotechnol Biol Med. 2011;7:780. doi: 10.1016/j.nano.2011.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Van Der Pol E, Hoekstra AG, Sturk A, Otto C, Van Leeuwen TG, Nieuwland R. Optical and nonoptical methods for detection and characterization of microparticles and exosomes. J Thromb Haemostasis. 2010;8:2596. doi: 10.1111/j.1538-7836.2010.04074.x. [DOI] [PubMed] [Google Scholar]
- 17.Gardiner Chris, Dragovic Rebecca. In: Extracellular Vesicles in Health and Disease. Harrison Paul, Gardiner Chris, Sargent Ian L., editors. Pan Stanford; Singapore: 2014. p. 261. [Google Scholar]
- 18.Boyd Robert D, Pichaimuthu Siva K, Cuenat Alexandre. New approach to inter-technique comparisons for nanoparticle size measurements; using atomic force microscopy, nanoparticle tracking analysis and dynamic light scattering. Colloids Surf A. 2011;387:35. [Google Scholar]
- 19.Bostrom M, Williams DRM, Ninham BW. Specific Ion Effects: Why DLVO Theory Fails for Biology and Colloid Systems. Phys Rev Lett. 2001;87:168103. doi: 10.1103/PhysRevLett.87.168103. [DOI] [PubMed] [Google Scholar]
- 20.Schein Perry, Ashcroft Colby K, O’Dell Dakota, Adam Ian S, DiPaolo Brian, Sabharwal Manit, Shi Ce, Hart Robert, Earhart Christopher, Erickson David. Near-field light scattering techniques for measuring nanoparticle-surface interaction energies and forces. J Lightwave Technol. 2015;33:3494. doi: 10.1109/JLT.2015.2440216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schein Perry, Kang Pilgyu, O’Dell Dakota, Erickson David. Nanophotonic force microscopy: Characterizing particle-surface interactions using near-field photonics. Nano Lett. 2015;15:1414. doi: 10.1021/nl504840b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Saveyn Hans, De Baets Bernard, Thas Olivier, Hole P, Smith J, Van Der Meeren Paul. Accurate particle size distribution determination by nanoparticle tracking analysis based on 2-D Brownian dynamics simulation. J Colloid Interface Sci. 2010;352:593. doi: 10.1016/j.jcis.2010.09.006. [DOI] [PubMed] [Google Scholar]
- 23.Erickson David, Serey Xavier, Chen Yih-Fan, Mandal Sudeep. Nanomanipulation using near field photonics. Lab Chip. 2011;11:995. doi: 10.1039/c0lc00482k. [DOI] [PubMed] [Google Scholar]
- 24.Schmidt Bradley S, Yang Allen HJ, Erickson David, Lipson Michal. Optofluidic trapping and transport on solid core waveguides within a microfluidic device. Opt Express. 2007;15:14322. doi: 10.1364/oe.15.014322. [DOI] [PubMed] [Google Scholar]
- 25.Lindner Moshe, Nir Guy, Vivante Anat, Young Ian T, Garini Yuval. Dynamic analysis of a diffusing particle in a trapping potential. Phys Rev E. 2013;87:022716. doi: 10.1103/PhysRevE.87.022716. [DOI] [PubMed] [Google Scholar]
- 26.El-Desouki Munir, Deen M Jamal, Fang Qiyin, Liu Louis, Tse Frances, Armstrong David. CMOS image sensors for high speed applications. Sensors. 2009;9:430. doi: 10.3390/s90100430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Banerjee Arindam, Kihm Kenneth D. Experimental verification of near-wall hindered diffusion for the Brownian motion of nanoparticles using evanescent wave microscopy. Phys Rev E. 2005;72:042101. doi: 10.1103/PhysRevE.72.042101. [DOI] [PubMed] [Google Scholar]
- 28.Bevan Michael A, Prieve Dennis C. Hindered diffusion of colloidal particles very near to a wall: Revisited. J Chem Phys. 2000;113:1228. [Google Scholar]
- 29.Sharma Prerna, Ghosh Shankar, Bhattacharya S. A high-precision study of hindered diffusion near a wall. Appl Phys Lett. 2010;97:104101. [Google Scholar]
- 30.Kang Pilgyu, Schein Perry, Serey Xavier, O’Dell Dakota, Erickson David. Nanophotonic detection of freely interacting molecules on a single influenza virus. Sci Rep. 2015;5:12087. doi: 10.1038/srep12087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kelly K Lance, Coronado Eduardo, Zhao Lin Lin, Schatz George C. The optical properties of metal nanoparticles: The influence of size, shape, and dielectric environment. J Phys Chem B. 2003;107:668. [Google Scholar]
- 32.Sbalzarini Ivo F, Koumoutsakos Petros. Feature point tracking and trajectory analysis for video imaging in cell biology. J Struct Biol. 2005;151:182. doi: 10.1016/j.jsb.2005.06.002. [DOI] [PubMed] [Google Scholar]


