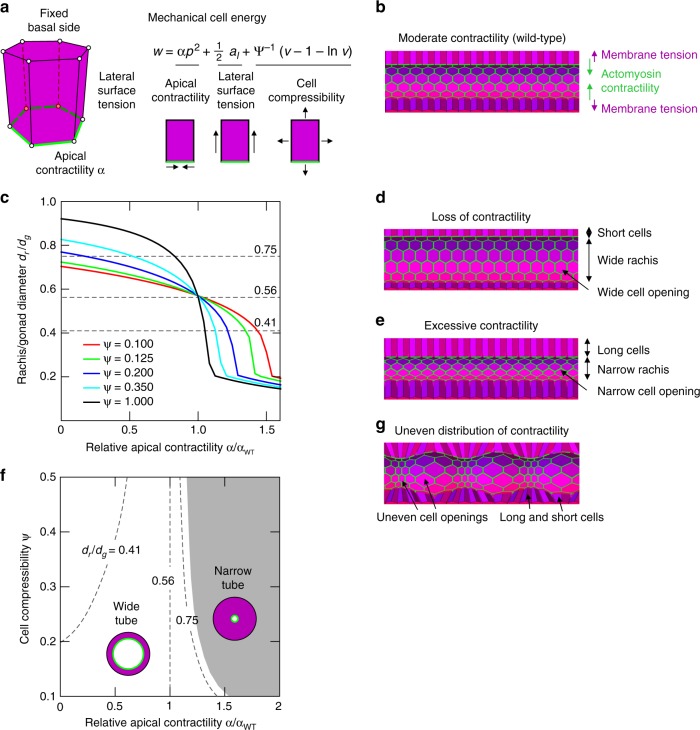
Fig. 7.

Mathematical model encapsulating the idea that syncytial germline architecture is regulated by contractile tension at the apical end of germ cells. a A three-dimensional computational model of the germline is based on 3D vertex model, where individual cells are modeled as polyhedral bodies with a polygonal base and apex. Forces were calculated from the prescribed potential energy w, which includes tension contributions from lateral cell surfaces, apical contractility, and cell compressibility. b Simulated germline tube morphologies at equilibrium for apical contractility α = 0.242 at fixed compressibility, ψ = 0.38. c Rachis diameter relative to the gonad diameter d_r/d_g at equilibrium as a function of the relative apical contractility α/α_WT (where α_WT is apical contractility for wild type) is shown for varying values of cell compressibility ψ. The dashed lines at d_r/d_g = 0.75, 0.56, and 0.41 correspond for the three distinct phenotypical morphologies. d Simulated germline tube morphologies at equilibrium for apical contractility α = 0.121 at fixed compressibility, ψ = 0.38. e Simulated germline tube morphologies at equilibrium for apical contractility α = 0.2701 at fixed compressibility, ψ = 0.38. f Morphological phase diagram of the model tubular epithelium exhibits two distinct regimes: wide-tube and narrow-tube morphologies. Isolines connect morphologies that correspond to the experimentally measured average rachis diameters from cyk-1/formin mutant (dr/dg = 0.75), wild-type (dr/dg = 0.56) and mel-11(RNAi) (dr/dg = 0.41) worms. g Equilibrium tube morphology observed for an imposed contractile modulation along the apical boundary along the tube’s axis for fixed compressibility, ψ = 0.38. The imposed modulation is 0.5α_WT sin (2πz/λ), where z is the longitudinal coordinate of the tube and λ is the tube’s length