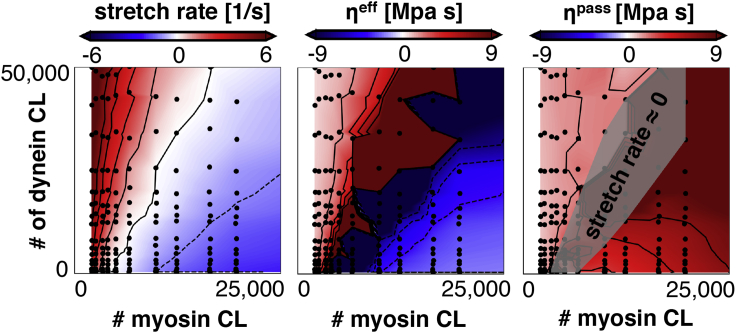
Figure 6.

Contour plots of stretch rate $\dot{\lambda }$, effective viscosity ${\eta }^{\text{eff}}$, and passive viscosity ${\eta }^{\text{pass}}$ as a function of the total number of myosin and dynein proteins in our computational model. The competition between dynein and myosin is apparent as the axon stretch rate increases with the number of dynein proteins and decreases with the number of myosin proteins. The effective viscosity, ${\eta }^{\text{eff}}=F^{\text{ext}}/\left[\dot{\lambda }A\right]$, approaches ${\eta }^{\text{eff}}\to \pm \infty$ when the axon stretch rate approaches zero, characteristic for active solids and fluids (5). Note that this phenomenon arises when internal forces balance external forces such that the axon does not extend or contract. This lack of motion results in an effective viscosity that approaches infinity. The passive viscosity, ${\eta }^{\text{pass}}$, increases with the total number of dynein and myosin, consistent with previous findings (5). We added a gray patch over the contour for passive viscosity where the stretch rate is approximately zero. In this region, the effective viscosity approaches $\pm \infty$ and, therefore, the computation for passive viscosity will be inaccurate. Each black dot in the contour plots represents one set of input parameters for the computational model. To account for the randomness in our computational model, we computed the average of n = 10 simulations to obtain each computational data point. To view this figure in color, go online.