Microtubules Provide a Viscoelastic Resistance to Myocyte Motion

Abstract

Background: Microtubules (MTs) buckle and bear load during myocyte contraction, a behavior enhanced by post-translational detyrosination. This buckling suggests a spring-like resistance against myocyte shortening, which could store energy and aid myocyte relaxation. Despite this visual suggestion of elastic behavior, the precise mechanical contribution of the cardiac MT network remains to be defined.

Methods: Here we experimentally and computationally probe the mechanical contribution of stable MTs and their influence on myocyte function. We use multiple approaches to interrogate viscoelasticity and cell shortening in primary murine myocytes in which either MTs are depolymerized or detyrosination is suppressed and use the results to inform a mathematical model of myocyte viscoelasticity.

Results: MT ablation by colchicine concurrently enhances both the degree of shortening and speed of relaxation, a finding inconsistent with simple spring-like MT behavior and suggestive of a viscoelastic mechanism. Axial stretch and transverse indentation confirm that MTs increase myocyte viscoelasticity. Specifically, increasing the rate of strain amplifies the MT contribution to myocyte stiffness. Suppressing MT detyrosination with parthenolide or via overexpression of tubulin tyrosine ligase has mechanical consequences that closely resemble colchicine, suggesting that the mechanical impact of MTs relies on a detyrosination-dependent linkage with the myocyte cytoskeleton. Mathematical modeling affirms that alterations in cell shortening conferred by either MT destabilization or tyrosination can be attributed to internal changes in myocyte viscoelasticity.

Conclusions: The results suggest that the cardiac MT network regulates contractile amplitudes and kinetics by acting as a cytoskeletal shock-absorber, whereby MTs provide breakable cross-links between the sarcomeric and nonsarcomeric cytoskeleton that resist rapid length changes during both shortening and stretch.

Introduction

The proliferation of microtubules (MT) and their post-translational detyrosination (dTyr) correlates with declining cardiac function (1, 2, 3, 4). Recently, we observed that MTs buckle in a sinusoidal fashion during myocyte contraction, suggesting a spring-like mechanism that could resist compression and possibly provide restoring force to facilitate cardiac relaxation. MT buckling relies on post-translational dTyr (for review of the tyrosination cycle, see (5)), which facilitates interaction between MTs and the cardiac sarcomere (2) and is associated with MT stability (6).

Although MT buckling provides visual evidence suggestive of an elastic resistance to contraction, previous efforts to pin down the mechanical contribution of MTs have produced inconsistent results. Magnetic twisting cytometry and single-cell shear measurements show that MTs provide both viscous and elastic rigidity to the cardiomyocyte (7, 8, 9). In contrast, measurements of steady-state elasticity by myocyte stretch have shown a small (10) or insignificant (7) role of the MT network in axial stiffness. Multiple groups have observed increased contractility with MT destabilization (11, 12, 13), which is most often attributed to decreased mechanical resistance, but this finding has not been supported by all (14).

Altered calcium handling must also be considered, as MTs mediate the mechanotransduction of calcium signals (15, 16) and the transport of proteins required for normal excitation-contraction (EC) coupling (17, 18). Pharmaceutical ablation of MTs was reported to increase the calcium transient during EC coupling (19), but this has been challenged by multiple groups whose work showed no effect of MT destabilization on EC coupling (16, 20). Recent work showed that reducing MT-dTyr similarly enhances myocyte contractility and reduces myocyte stiffness without grossly affecting EC coupling (2). In diseased myocytes, for which a proliferated MT network likely plays a more significant mechanical role, MT destabilization has been shown to enhance myocyte contractility independent of a change in the calcium transient (4, 21). Thus, despite apparent conflicting results, increased mechanical compliance remains a sensible explanation for the enhanced contractility observed upon MT destabilization, but it remains to be clearly demonstrated how an enhancement in contractility may arise from a reduction in MT-dependent stiffness.

This study aims to dissect the precise role that MTs and MT-dTyr play in cardiomyocyte viscoelasticity (VE) and to determine whether altered VE is sufficient to explain changes in myocyte contraction. To this end, we paired calcium and contractility measurements with high-sensitivity VE analysis using transverse nanoindentation and tensile stress-relaxation tests. We find that MT tyrosination or depolymerization similarly amplifies and accelerates contractility independent of a change in calcium handling. VE measurements that inform computational modeling suggest these changes can be completely accounted for by measured reductions in myocyte VE, whereas they cannot be explained by changes in passive stiffness or elasticity alone.

Methods

This study was conducted on freshly isolated adult ventricular myocytes from Sprague Dawley rats. All experiments were performed immediately after cell isolation with the exception of adenoviral (AdV)-treated myocytes.

Animal models

All animal care and experimental procedures were approved and performed in accordance with the ethical standards set forth by the Institutional Animal Care and Use Committee of the University of Pennsylvania and by the National Institutes of Health. Rats (Sprague Dawley) were purchased from Harlan Laboratories (Indianapolis, IN).

Myocyte isolation and culture

Primary adult ventricular myocytes were isolated from 8- to 12-week-old Sprague Dawley rats as previously described (15). In summary, rats anesthetized under isoflurane received an intramuscular injection of heparin (∼1000 units/kg) before the heart was excised and cannulated for retrograde perfusion with enzymatic digestion solution at 37°C on a Langendorff apparatus. Digested hearts were then minced and triturated with glass pipettes to isolate individual cardiomyocytes. Isolated myocytes were gently centrifuged (300 rotations per minute) to remove debris and gradually reintroduced into rat cardiomyocyte (RCM) medium (formulation below).

After isolation, cells in RCM medium with 25 μM cytochalasin D were plated at low density into 12 well plates and treated with viral constructs. Viral constructs were expressed for 48 h with multiplicity of infection = 100–200 of AdV-tubulin tyrosine ligase (TTL)-IRES-dsRed as previously described (2), and experiments were conducted on the second day after isolation. Freshly isolated myocytes were diluted 5× from RCM medium into normal Tyrode’s (NT) solution and treated with 10 μM of either colchicine or parthenolide (PTL). Experiments were conducted after 1.5 h drug treatment in the presence of 10 μM colchicine or PTL. All experiments and culture on RCMs were conducted in the presence of 1.8 mM Ca²⁺.

For RCM Medium, Medium 199 (11150-59; GIBCO, Waltham, MA) was supplemented with 1× insulin-transferrin-selenium-X (51500-56; GIBCO), 20 mM HEPES (pH 7.4), and 0.1 mg/mL Primocin.

NT solution was 140 mM NaCl, 0.5 mM MgCl2, 0.33 mM NaH2PO4, 5 mM HEPES (pH 7.4), 5.5 mM glucose, and 5 mM KCl titrated to a pH of 7.4 with 1 M NaOH.

Cell stretch

Experiments were performed in custom-fabricated glass-bottom petri dishes mounted on an LSM Zeiss 880 (Carl Zeiss AG, Oberkochen, Germany) inverted confocal microscope using a 40× oil 1.4 NA objective and transmitted light camera (MyoCam-S; IonOptix, Westwood, MA). Cell stretch experiments were carried out as previously described (2). Cells were attached to glass holders with a laser-etched cavity via MyoTak (Ionoptix) adhesive. One cell holder was connected to a piezoelectric length controller and the other to a high-sensitivity optical force transducer (OFT-100; IonOptix). Force and sarcomere length (SL) were continuously recorded at 1 kHz. Cells with a resting SL below 1.7 μm were considered hypercontracted and discarded from these studies. Force and SL traces were analyzed in IonWizard (IonOptix).

Calcium and contractility measurements

Myocytes were loaded by 15 min incubation at 1 μM Fluo-4-acetoxymethyl ester (Invitrogen, Carlsbad, CA). Imaging was conducted in confocal line scan mode with a 488-nm argon ion laser at 0.909 ms/line. Cells were electrically paced (MYP100, IonWizard; IonOptix) at 1 Hz for 20 s to achieve steady state; the final five traces of the pacing protocol were pooled and analyzed for calcium transient properties. The measured fluorescence (F) throughout the transient was normalized to the resting fluorescence before stimulation (F₀) to normalize for heterogeneity in dye loading. Simultaneously, SL was measured optically by Fourier transform analysis (IonWizard; IonOptix), and during 20 s of pacing, the final five traces were again recorded and averaged using IonWizard.

Nanoindentation

Mechanical properties at the microscopic scale were measured using nanoindentation (Piuma; Optics11, Amsterdam, The Netherlands). Freshly isolated human myocytes were attached to glass-bottom dishes coated with MyoTak (IonOptix) in NT solution at 1 mM Ca²⁺. A spherical indentation probe with a radius of 3.05 μm and a stiffness of 0.026 N/m was used. Myocytes were indented to a depth of 2.5–3.5 μm with velocities of 0.1, 0.25, 0.5, 1.0, 2.0, 5.0, 10.0, 20.0, 50.0, 100.0, and 150.0 μm/s. The tip was held in this indentation depth for 1 s and retracted over 2 s. The Young’s moduli were calculated automatically by the software by fitting the force versus indentation curve to the Hertz equation. The Young’s modulus E is derived from the fit of the initial 60% of the loading force-displacement curve (F(h)), the indenter tip radius (R), and indentation depth (h), according to the following formula, for which a Poisson’s ratio (ν) of 0.5 was assumed.

$$F\left(h\right)=\frac{4}{3}\frac{E}{\left(1-{\nu }^2\right)}{R}^{1/2}{h}^{3/2}$$ (1)

The average of E in each condition with standard error is plotted against different indentation speed. Low-velocity indentation measures elastic contributions (E_min) to stiffness, and high-velocity indentation measures elastic and viscous contributions (E_max). The change in modulus with rate represents myocyte viscoelasticity (ΔE). To fit Young’s modulus versus indentation-rate plots to the VE model, indentation velocity was converted to indentation frequency using the average indentation depth at each rate. The VE model could then be solved as a function in indentation frequency, allowing the VE constants E₁, E₂, η₁, and η₂ to be determined from the fit of the expression below, where the “frequency,” f, is the indentation velocity divided by the indentation depth (21).

$$E\left(f\right)=\frac{E_1{E}_2+\left(E_1+E_2\right){\eta }_{2}f+E_2{\eta }_{1}f+{\eta }_1{\eta }_2{f}^2}{E_2+{\eta }_{2}f}$$ (2)

Statistical analysis

Statistical analysis and graphing were performed with OriginLab 9.0. Values are presented as means ± standard error in bar and line graphs. Dot plots show SD as whiskers and mean line. When comparisons between sets were both repetitive and restricted, the Bonferroni multiple comparisons correction was used to adjust the significance threshold of two-sided t-tests accordingly. One-way analysis of variance (ANOVA) with post hoc Tukey test was used to correct for multiple comparisons sharing a single control condition.

Mathematical model for myocyte contractility

For stress exerted by the contractile unit during the contractile timescale, σ(t), the strain response, ε(t) = ΔSL/SL_o(t), can be analytically determined by solving the strain response of the VE model proposed in Fig. 2 D, which is a Kelvin-Voigt VE element in parallel configuration with a Maxwell element. The total stress exerted by the sarcomeric units is distributed equally over the parallel units in the model by their corresponding stress-strain relationship.

$$\sigma \left(t\right)={\eta }_1\dot{\mathit{ϵ}}\left(t\right)+E_1\mathit{ϵ}\left(t\right)+\frac{E_2{\eta }_2\mathit{ϵ}\left(t\right)\dot{\mathit{ϵ}}\left(t\right)}{E_2\mathit{ϵ}\left(t\right)+{\eta }_2\dot{\mathit{ϵ}}\left(t\right)}$$ (3)

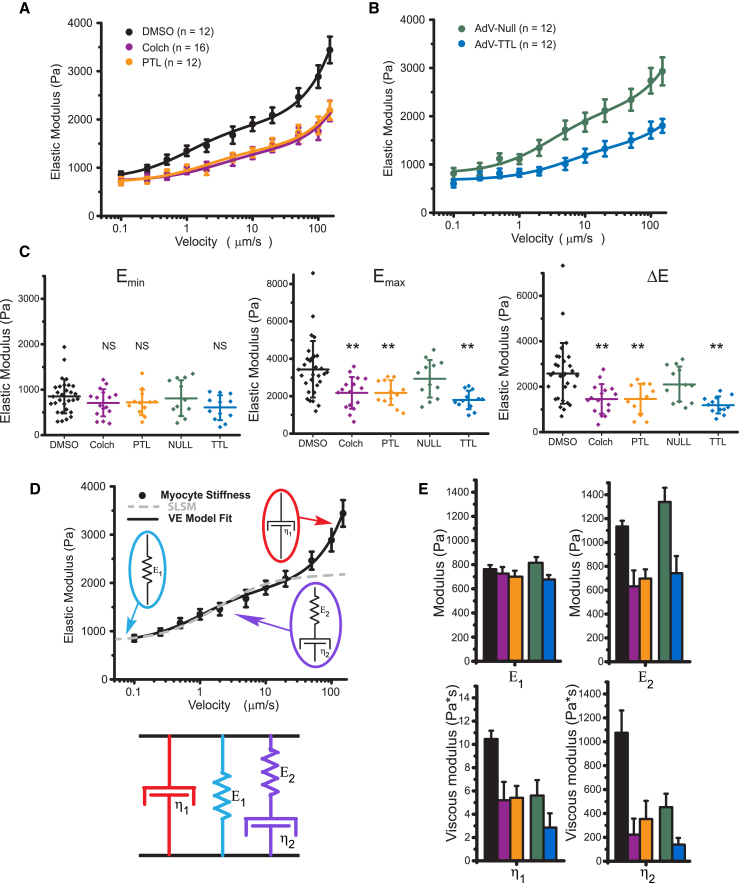
Figure 2.

Transverse indentation at variable rates to assess myocyte viscoelasticity. (A) Young’s modulus versus indentation velocity in freshly isolated RCMs treated with DMSO, colchicine, or PTL. Data points are means with standard error whiskers. (n = 12, 16, and 12 cells from three rats for DMSO, colchicine, and PTL, respectively). (B) Young’s modulus versus indentation velocity in RCMs 48 h post-transfection with AdV-Null, green, or AdV-TTL, blue. Data points are means with standard error whiskers. (n = 12 cells from three rats for both AdV-Null and AdV-TTL.) Solid lines in both (A) and (B) are best-fit curves to the VE model shown in (D). (C) The minimal Young’s modulus, E_min, is determined by the cell stiffness at the slowest (100 nm/s) indentation rate. The maximal Young’s modulus, E_max, is determined by the cell stiffness at the fastest (150 μm/s) indentation rate. The change in Young’s modulus over the velocity range measured, ΔE, is determined by E_max − E_min for each cell. Statistical significance was determined by one-way ANOVA with post hoc Tukey as ^∗p < 0.05, ^∗∗p <0.01, or ^∗∗∗p < 0.001 compared to DMSO or AdV-Null. Dot plots show mean line and whiskers as SD. (D) The VE model (a Maxwell element in parallel configuration with a Voigt element; below) for which the velocity-dependence of Young’s modulus can be fitted to extract the stiffness of each element (black trace). The dashed trace illustrates the velocity dependence of the Young’s modulus for a standard linear solid model fitted to the data and provides justification for the inclusion of the additional viscous element (η₁). (E) VE parameters extracted from model fitted to data in (A) and (B). Bar plots show the estimated fitted value with whiskers showing the fit certainty. To see this figure in color, go online.

Simplifying the expression for stress and strain yields the second-order ordinary differential equation (ODE) below.

$${\eta }_1{\eta }_2\ddot{\mathit{ϵ}}\left(t\right)+\left(E_2{\eta }_2+E_1{\eta }_1+E_2{\eta }_1\right)\dot{\mathit{ϵ}}\left(t\right)+E_1{E}_2\mathit{ϵ}\left(t\right)=E_2\sigma \left(t\right)+{\eta }_2\dot{\sigma }\left(t\right)$$ (4)

This is a second-order ODE of the form

$$a{y}^{″}\left(t\right)+b{y}^{\prime }\left(t\right)+cy\left(t\right)=G\left(t\right),$$ (5)

where

$$G\left(t\right)=E_2\sigma \left(t\right)+{\eta }_2\dot{\sigma }\left(t\right).$$ (6)

Thus, for an arbitrary input stress, G(t) can be determined. The solution for $\mathit{ϵ}\left(t\right)$ to the ODE (Eq. 5) is written explicitly in terms of elastic elements as follows:

$$\epsilon \left(t\right):=\left[\frac{\left[{\int }_0^t{e}^{\left[\left[\frac{\text{b}}{2\text{a}}-\left(\frac{\sqrt{{\text{b}}^2-4\text{a}\times \text{c}}}{2\text{a}}\right)\right]\text{t}\right]}\times \text{G}\left(\text{t}\right)\text{dt}\right]\times e^{\left[\left(\frac{-\text{b}}{2\text{a}}-\frac{\sqrt{{\text{b}}^2-4\text{a}\times \text{c}}}{2\text{a}}\right)\text{t}\right]}-\left[{\int }_o^t{e}^{\left[\left(\frac{\text{b}}{2\text{a}}-\frac{\sqrt{{\text{b}}^2-4\text{a}\times \text{c}}}{2\text{a}}\right)\text{t}\right]}\times \text{G}\left(\text{t}\right)\text{dt}\right]\times e^{\left[\left[\frac{-\text{b}}{2\text{a}}-\left(\frac{\sqrt{{\text{b}}^2-4\text{a}\times \text{c}}}{2\text{a}}\right)\right]\text{t}\right]}}{\sqrt{{\text{b}}^2-4\text{a}\times \text{c}}}\right],$$ (7)

where

$$a={\eta }_1{\eta }_2,$$

$$b=E_2{\eta }_2+E_1{\eta }_1+E_2{\eta }_1,$$

and

$$c=E_1{E}_2.$$

The limitations of the model require that the solution be real, i.e., b² > 4ac, and solvable, i.e., a > 0. Consequently, the solution is valid only when each element has a finite positive value. This is reasonable, considering we are interested in modeling the case in which all of the elements have a contribution to the mechanics. Further, to estimate the timescale of the force relative to the calcium transient, we chose the function (Fig. 5 A) that has a shape (rise and decay parameters) that we felt was consistent with the force that would be generated by the measured calcium transients.

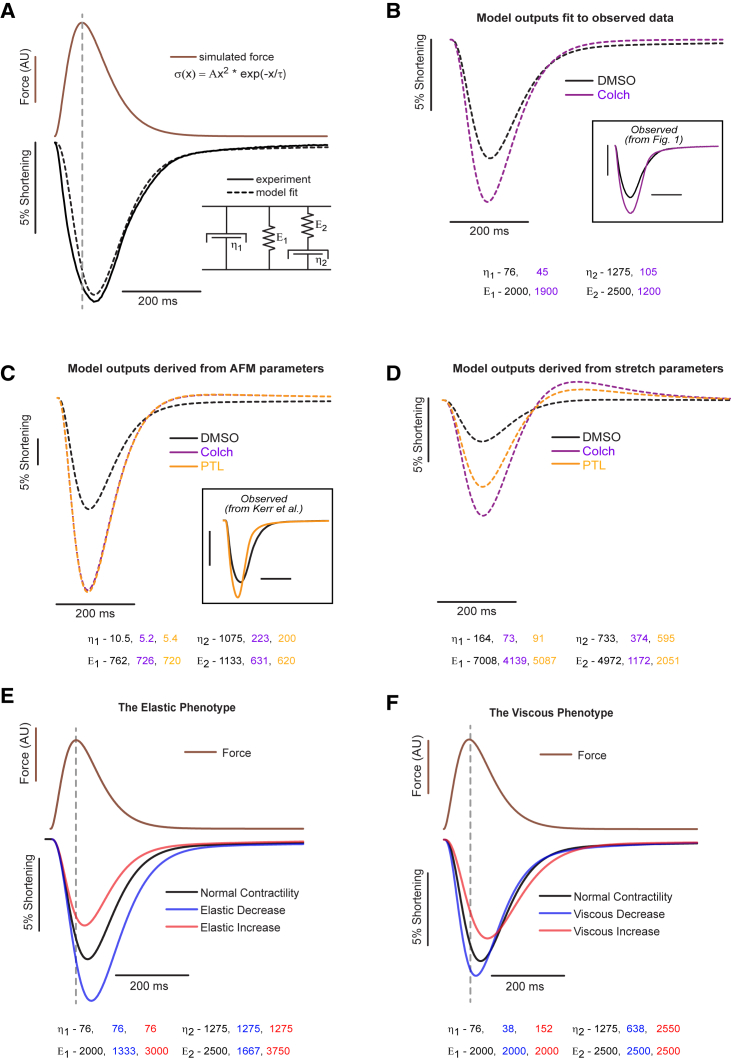
Figure 5.

VE model of cardiomyocyte contractility. (A) The stress-strain relationship defined by the VE model (bottom right inset) converts myofilament force (brown) to shortening (black dotted trace). By changing the stiffness of individual VE elements (values are shown in (B), bottom), experimentally observed shortening (black solid trace) can be modeled (black dashed trace) by cytoskeletal viscoelasticity. (B) Model fits (dashed traces) to observed DMSO and colchicine contractility data (boxed inset). Best-fit parameters are shown below the plot. (C) Modeled contractility from VE parameters derived from transverse indentation studies (Fig. 2). Previously observed data for PTL treatment are provided for comparison (inset). (D) Modeled contractility from parameters derived from tensile tests (Fig. 3). (E) Simulated changes in contractility for myocyte for which there is an isolated reduction (blue) or increase (red) in myocyte elasticity. (F) Simulated changes in contractility for which myocyte viscosity has been decreased (blue) or increased (red). To see this figure in color, go online.

Wolfram Alpha was used to determine the solution for the ODE, and Mathcad 14.0 (PTC, Needham, MA) was used to generate the analytical model relating the VE parameters to contractility (strain, ε(t)).

Results

Depolymerizing MTs enhances contractile and relaxation velocity

We collected paired calcium and contractility transients on RCMs treated with colchicine (Fig. 1) immediately after cell isolation. As shown in Fig. 1 A, the calcium transient is largely unaffected by treatment with colchicine (purple). Peak calcium, rise times, and decay times are not significantly different in colchicine-treated cells (Fig. 1 B). In contrast, myocyte contractility is enhanced by colchicine (Fig. 1 C). Resting SL is unchanged (∼1.83 μm, Table S1), but fractional shortening is significantly increased. The increased fractional shortening occurs over a similar timescale (Fig. 1 D), leading to higher peak contractile and relaxation velocities for colchicine-treated cells (Fig. 1 F). Thus, colchicine can increase the contractility of RCMs independent of an increase in [Ca²⁺]_i, suggesting that MT depolymerization affects the rate at which myocytes can change their length under a similar level of activating [Ca²⁺]_i.

Figure 1.

MT depolymerization enhances myocyte contractility. (A) Normalized calcium transient (F/F_o) for control (black) and colchicine-treated (purple) cells. (B) Peak calcium, time to peak, and decay time determined from individual traces (N = 6 hearts, n = 43 dimethylsiloxane vehicle (DMSO) cells, n = 48 colchicine-treated cells). (C) Relative shortening (change in SL divided by resting SL) with time. (D) Peak shortening, shortening, and relaxation times from individual traces from identical cells analyzed in (B). (E) The average shortening velocity for DMSO- and colchicine-treated RCMs from (A) and (C). (F) Peak shortening and relaxation velocity determined for individual data points. Statistical significance was determined as *p<0.05, ^∗∗p < 0.01 or ***p <0.001 compared to DMSO, Student’s t-test. (G) A comparison of changes in contractile velocities and fractional shortening upon various manipulations to depolymerize MTs or alter MT-dTyr. Each treatment condition is displayed normalized to its relative control (for example, DMSO treated for PTL or a null-encoding adenovirus (AdV-Null) for AdV-TTL). Colchicine data are from the current study. PTL and taxol data are replotted from (16). TTL overexpression and knock-down data are replotted from (2). Data in (Β), (D), (F), and (G) are means with standard error bars. To see this figure in color, go online.

A quantitatively similar calcium-independent enhancement of contractility has been observed when post-translational dTyr of the MT network is suppressed (Fig. 1 G) (2, 16). This system can be pushed in both directions because myocyte contraction is reduced and prolonged when MT density or dTyr is increased (Fig. 1 G). If mechanical in origin, the concurrent increase in contractile and relaxation velocity associated with a reduction in MTs or MT-dTyr points toward a viscous or VE role for dTyr MTs. This is in contrast to a purely elastic mechanical role, in which an increased fractional shortening would accompany a prolonged contractile timescale. Thus, our data here and in recent work predict a viscous role for dTyr MTs in resisting myocyte length change.

Depolymerizing or tyrosinating MTs similarly reduces myocyte viscoelasticity

To determine the contribution of stable MTs to cardiomyocyte mechanical properties, transverse indentation was performed at variable speeds to obtain a VE profile of the cell and to extract generalized VE parameters (22). Fig. 2, A and B show Young’s modulus as a function of indentation velocity. The increase in myocyte stiffness with indentation velocity confirms that cardiomyocytes are VE. Further, the data can be used to derive a generalized viscoelastic model (fitted by solid lines), for which the simplest model that fits the data is depicted in Fig. 2 D, consisting of a spring, dashpot, and Maxwell element in parallel. The spring E₁ describes the steady-state stiffness, the spring E₂ becomes engaged at timescales faster than η₂/E₂ but dissipates stored energy if compressed for longer, and the viscous element η₁ approximates cytoplasmic viscosity, which accounts for the upward trend of modulus at rates >50 μm/s.

Colchicine-treated cardiomyocytes are still VE and exhibit a similar steady-state stiffness (E_min, Fig. 2 C) as untreated cells. The stiffness of colchicine-treated cells increases less with indentation rate, indicating a reduction in viscoelasticity (ΔE, Fig. 2 C). The difference in stiffness becomes significant at indentation rates >500 nm/s, and the total change in modulus over the velocity range tested (ΔE) is significantly less for colchicine-treated cells (Fig. 2 E). Using the VE model to derive the stiffness of individual elements, the steady-state elasticity, E₁, is not different for colchicine-treated cells, whereas VE parameters, E₂, η₁, and η₂ are all significantly reduced (Fig. 2 E). This is consistent with the MT network engaging with the surrounding structure in the myocyte through cross-links (2) that slip (and thus do not contribute to mechanical properties) on a timescale approximated by η₂/E₂, or ∼1 s.

Previous work suggested a decrease in VE upon MT tyrosination by TTL overexpression, but restricted indentation depth (<500 nm) limited measurement sensitivity to submembrane cortical stiffness (2). Thus, indentation of RCMs treated with PTL or overexpressing TTL are here performed at a greater indentation depth (3 μm). A decrease in VE nearly identical to that of colchicine treatment is observed when MTs are tyrosinated, whereby E_min is not different compared to the respective control, whereas E_max and ΔE are significantly decreased (Fig. 2, C and E). No significant differences in stiffness between colchicine- and PTL-treated myocytes are observed, which is consistent with a dTyr-dependent engagement of MTs with the sarcomeric cytoskeleton forming the basis of their contribution to myocyte viscoelasticity.

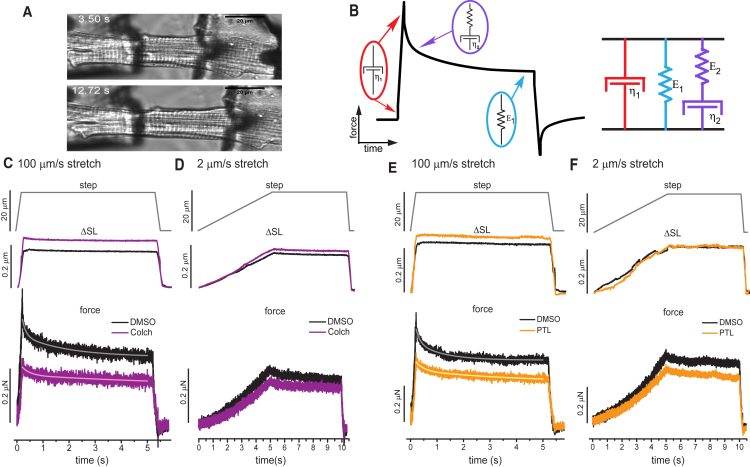
Recognizing that myocytes are anisotropic and nanoindentation probes only the transverse axis, single-cell tensile tests (axial stretch) were conducted to determine the mechanical contribution of the MT cytoskeleton along the contractile axis. Immediately after isolation, we stretched myocytes at different rates to determine the contribution of strain rate to stiffness, and VE was determined by a 5 s isometric hold to evaluate stress relaxation. Fig. 3, C–F show the position of the length controller (top row), the corresponding change in SL applied to the cell (ΔSL, second row), and the measured force recorded (third row) as a function of time. In the 100 μm/s stretch, the force transient exhibits a peak followed by a rapid decay (τ = 200 ms) and then a slow relaxation toward a steady-state value (Fig. 3 C). The peak force and the magnitude of the relaxation (Fig. 3, C and E) are reduced by both colchicine and PTL treatment, indicating a reduction in viscoelasticity. In contrast, in 2 μm/s stretches, significant stress relaxation is not observed irrespective of treatment group, and the relaxation during the isometric hold is not significant or affected by colchicine or PTL (Fig. 3, D and F).

Figure 3.

For a Figure360 author presentation of Fig. 3, see the figure legend at https://doi.org/10.1016/j.bpj.2018.9.019#mmc3

Axial stretch at variable rates after colchicine and PTL treatment of RCMs. (A) A transmitted light image of isolated adult RCM before and during tensile test. (B) The VE model (a Maxwell element in parallel configuration with a Voigt element) for which the time dependence of the stress-strain curve can be used to extract values for each parameter. The top row shows the imposed length change—a 20 μm length controller step over either a 200 ms (C and E) or 5 s (D and F) stretch, followed by a 5 s hold and 200 ms return. The middle row shows the average change in SL in response to stretch. The bottom row shows the average change in force in response to stretch. (A and B) 100 μm/s stretch and 2 μm/s stretch for DMSO and colchicine (N = 5 hearts, n = 17 cells DMSO, n = 18 cells colchicine). (C and D) 100 μm/s stretch and 2 μm/s stretch for DMSO and PTL. (N = 5 hearts, n = 14 cells DMSO, n = 17 cells colchicine). Solid traces overlaid on force-relaxation curves are best fits to double exponential decay function. To see this figure in color, go online.

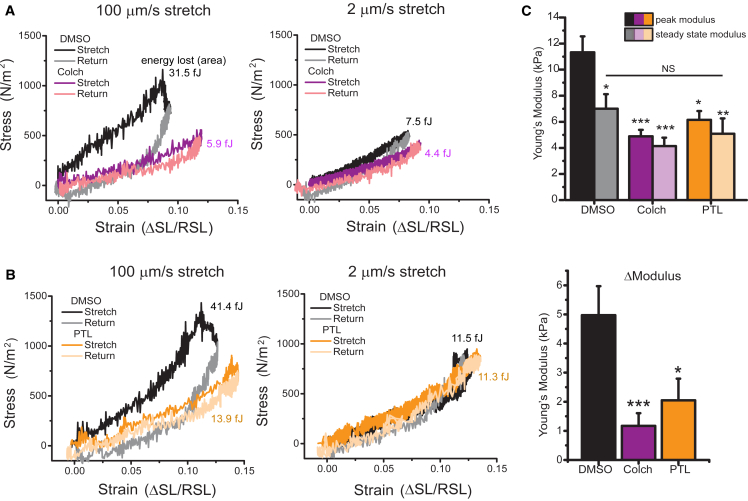
Cardiomyocyte Young’s modulus at each strain rate was determined from the slope of the stress (force divided by myocyte cross-sectional area) versus strain (ΔSL/resting SL) curve (Fig. 4). The area between the stretch (dark traces) and return (light traces) is an approximation of the amount of energy (work) lost to viscosity during each stretch. The average Young’s modulus of each condition is indicated by the slope of the stress-strain curves, and peak and steady-state moduli for individual myocytes are presented in Fig. 4 C. The peak modulus is reduced by colchicine and PTL for the fast (100 μm/s) but not the slow (2 μm/s) stretch rate (Fig. 4, A and B). The energy lost to viscosity is significantly reduced by colchicine and PTL treatment under rapid stretch, whereas the slow stretch (which shows minimal energy dissipation and almost purely elastic behavior) is not significantly altered by colchicine or PTL. Thus, both tensile tests and transverse indentation indicate that colchicine and PTL treatment reduce myocyte VE, causing stiffness differences to be most pronounced at high strain rates. These findings are consistent with the contractility data in Fig. 1, which suggest a VE change in the cardiomyocyte due to concurrent increases in contractile amplitude and velocity that cannot be explained by differences in the calcium transient.

Figure 4.

Stress-strain curves calculated from axial stretch. (A) Stress-strain loops for DMSO- and colchicine-treated cells at 100 and 2 μm/s. (B) Stress-strain loops for DMSO- and PTL-treated cells at 100 and 2 μm/s. (C) Peak and steady-state modulus (top) and relaxation modulus (peak − steady state) (bottom) for individual cells treated with DMSO, PTL, or colchicine. Statistical significance was determined by one-way ANOVA with post hoc Tukey as ^∗p < 0.05, ^∗∗p < 0.01, or ^∗∗∗p < 0.001 compared to DMSO. To see this figure in color, go online.

The VE model derived from transverse indentation data (Fig. 2) can also be fitted to the axial stretch data (Figs. 3 and 4) to extract VE parameters along the contractile axis (Methods). Tables 1 and 2 show a comparison of VE parameters derived from the two orthogonal approaches; transverse indentation (Table 1) and passive length tension (Table 2). Generally, there are stiffer elastic components, a higher viscosity, and a faster relaxation time (τ = η₂/E₂) in the longitudinal versus transverse axis of the cell. This is consistent with an elastic spring element such as titin and a VE element such as the passive resistance of the myofilaments contributing more to the mechanical properties of the myocyte during axial stretch but not upon transverse indentation.

Table 1.

VE Parameters Derived from Transverse Indentation

Parameter	DMSO	Colchicine	PTL	AdV-Null	TTL
η1	10.5 ± 0.7	5.2 ± 1.6	5.4 ± 1	5.6 ± 1.3	2.9 ± 1.2
η2	1075 ± 187	223 ± 134	353 ± 152	452 ± 113	139 ± 56
E1	762 ± 34	726 ± 54	700 ± 49	815 ± 47	677 ± 37
E2	1133 ± 49	632 ± 134	697 ± 77	1339 ± 119	742 ± 144

Values are expressed as mean ± fit error.

Table 2.

VE Parameters Derived from Passive Length Tension

Parameter	DMSO	Colchicine	PTL	AdV-Null	TTL
η1	164 ± 15	73 ± 4	91 ± 12	–	–
η2	827 ± 193	434 ± 155	736 ± 232	–	–
E1	7108 ± 1111	4139 ± 644	5087 ± 1177	–	–
E2	4972 ± 998	1172 ± 434	2051 ± 743	–	–

Elasticities are expressed as mean ± standard error, and viscosities are expressed as mean ± fit error.

A VE model for contractility

We next generated a computational model to test if the observed changes in viscoelasticity can account for enhanced myocyte contractility upon MT destabilization (Fig. 1). Myocyte shortening (strain) was derived from the VE model (Fig. 2 D) to generate an analytical model that relates myofilament force production (internal stress) to myocyte length change (Fig. 5). Force production was approximated by the function shown in Fig. 5 A, for which the amplitude and decay constant, τ, determine the size and decay rate of the force. The force function is consistent with the shape and time course of developed tension in cardiac muscle (23). An identical force (amplitude and τ) was used throughout Fig. 5, based on the observation of similar Ca²⁺ transients (Fig. 1) and assumption of similar myofilament Ca²⁺ sensitivity. Adjusting the stiffness of the VE elements in the model to fit (dashed line) the contractility trace (black solid line) indicates that the VE model can accurately capture the contractile transient.

Fitting the VE model to the measured colchicine contractile transient provides a modeled estimate of the VE changes that occur in response to MT depolymerization (Fig. 5 B). The best fit values of the VE model to the contractility transients in Fig. 1 are shown below Fig. 5 B. Under identical force, the changes in cell shortening observed with colchicine treatment can be tightly reproduced by reducing the VE properties of the myocyte (η₁, η₂, and E₂). Simply changing the elastic properties (E₁) of the myocyte cannot recapitulate the change in both shortening amplitude and velocity (Fig. 5 E). Thus, the model agrees with experimental observations that increased contractile amplitude and velocity can be imparted by a decrease in myocyte viscoelasticity but not by elasticity alone.

Using the measured VE parameters obtained by transverse indentation or axial stretch (Fig. 5, C and D, bottom), the VE model qualitatively reproduces the alterations in myocyte shortening observed upon PTL or colchicine treatment. Quantitatively, indentation underestimates whereas axial stretch overestimates the myocyte stiffness felt during shortening, leading to a respective overestimate and underestimate of the degree of shortening predicted by the model. This disparity suggests that transverse indentation is more sensitive to probing viscoelasticity imparted by the nonsarcomeric cytoskeleton and underestimates the contribution of longitudinal components of the sarcomere such as titin and the myofilaments. This is consistent with fluorescent observation of the MT network deforming extensively during transverse indentation in the absence of sarcomere stretch (Video S1). Conversely, stiffness measured during axial stretch may be augmented by resting myofilament tension that is not anticipated to impact myocyte shortening.

Video S1. Nanoindentation of Rat Cardiomyocyte

AdV-EMTB 3x GFP transfected in culture for 48 h enabled MT imaging during nanoindentation. During indentation MTs deform significantly, while sarcomeres are not stretched. Two color overlay shows initial frame (pre-indentation) in blue and subsequent frames (during indentation) in orange. Colocalization appears white.

The model also predicts that viscous energy dissipation (damping) is important for regulating the contractile timescale of the myocyte. If the VE terms are outweighed by elasticity, the contractile timescale closely follows the time course of myofilament force generation, whereas the reduced contractile timescale imparted by VE reduction indicates that myocyte viscosity is sufficient to impact the contractile timescale of the unloaded myocyte. Consequently, there is likely a balance between elastic restoring forces and viscous damping in regulating myocyte contractility.

The model distinguishes between two contractile phenotypes that can arise from different mechanical underpinnings (Fig. 5, E and F). An elastic phenotype, as shown in Fig. 5 E, is characterized by changes in contractile amplitude proportional to changes in timescale. These changes would be signature of changes in myocyte restoring force (perhaps due to a change in titin/myofilament compliance), whereby an increase in restoring force reduces contractility but accelerates relaxation. Conversely, reducing the stiffness of series elastic elements increases contractility but extends the contractile timescale. On the other hand, viscous changes, as shown in Fig. 5 F, are characterized by changes in contractile amplitude that are inversely proportional to changes in the contractile timescale. Reducing myocyte viscosity, as is accomplished above by reducing MT-dTyr, enhances myocyte contractility while accelerating the contractile timescale, whereas increased viscosity reduces contractility but lengthens the contractile timescale. This is consistent with the idea that internal viscosity in the myocyte resists motion in both directions.

Discussion

Here, we find that VE resistance imparted by MTs is sufficient to impede cardiomyocyte motion. Myocytes have various mechanisms to regulate elastic and viscous characteristics—for example, changes in the stiffness of spring elements can occur by changes in titin isoform expression or post-translational modification (24, 25, 26). Our work, in conjunction with others, suggests that the MT network contributes viscosity to the myocyte (7, 8, 9). This contribution can be regulated by the density of the MT network or by certain post-translational modifications that can alter MT stiffness (acetylation) (27) or cross-linking with other cytoskeletal binding partners (dTyr) (2, 28). Herein, we show that post-translational dTyr of the MT network increases myocyte viscosity and that the pool of detyrosinated MTs largely accounts for the MT contribution to myocyte mechanics.

The mechanical role of MTs has been reported to be viscous (9), elastic (10), VE (8), and not significant (29) in cardiomyocytes. Our results help to reconcile these measurements, whereby the strain direction and rate determine how and whether MTs contribute significantly to myocyte stiffness. At slow strain rates, we find a small or insignificant change in MT-dependent mechanical properties, which is consistent with modest changes observed during previous measurements of resting stiffness (7, 10). At higher strain rates, we observe a significant contribution of the MT network that is consistent with a role in myocyte viscoelasticity. Our high-speed deformations are consistent with the strain rates experienced by the myocyte during the contractile cycle, specifically during diastolic filling. We complement our mechanical measurements and unloaded shortening measurements with computational modeling that quantitatively supports the idea that alterations in viscosity and viscoelasticity underlie the observed changes in myocyte mechanics.

Although previous studies have reported nonsignificant effects of colchicine on the contractility of healthy rat myocytes, the basal contractile velocity reported was less than half of what we obtained (20). A slower rate of contraction would diminish the viscous resistance of MTs and reduce the effect that MT depolymerization has on contractility. By the same standard, the slower contractile velocities in larger animal models may render MT resistance largely undetectable unless the MT network is significantly proliferated and detyrosinated, as it is in the case of disease (2, 3, 30), which is in agreement with the findings of Cooper et al. (11). Thus, although previous reports on MT mechanics at first appear contradictory, many of these findings are quite reconcilable when rate dependence is considered.

The potential physiological and pathophysiological consequences of MT-dependent viscosity warrant discussion. Our work shows that viscosity plays a significant role modulating the contractility of unloaded myocytes, but it is worth noting that internal viscosity will have its largest impact under low external loads. Regarding loaded muscle, although Fenn’s original studies suggested that striated muscle is highly elastic (31), even healthy cardiac muscle is far from 100% efficient and exhibits increased energetic cost to shorten at higher velocities (32, 33). This may be attributable to a combination of viscous energy dissipation and a velocity-dependent reduction of cross-bridge efficiency, as documented in skeletal muscle (33, 34). More recent observations that peak shortening consistently lags peak force production in cardiac tissue demonstrate a significant impact of viscosity (35). Although we tend to view MT-dependent viscosity as a negative regulator of myocardial energetics, it is worth considering that MT-dependent viscosity could dampen shortening velocity to actually improve cross-bridge efficiency, thus optimizing energy consumption under physiologic conditions.

The pathophysiological consequences of MT-dependent viscosity are perhaps more straightforward. Highly proliferated and detyrosinated MTs are frequently observed in failing hearts (4) and would reduce the work done during a contractile cycle by dissipating energy during phases of rapid volume change (36). Viscosity should exert its largest effect during periods of rapid length change and low load (35), which, during the cardiac cycle, best corresponds to myocyte relaxation and relengthening in diastole. The finding that the MT-polymerizing chemotherapeutic agent taxol impairs myocardial mechanics in patients by prolonging relaxation times and slowing filling velocities and strain rates (37) is consistent with this idea, but further in vivo studies and examination of the MT role in systolic and diastolic dysfunction are needed.

There are caveats to consider when interpreting our results. The experimental measurements and modeling are derived under the assumption of linearity. Muscle tissue exhibits clear nonlinear mechanical properties; thus, consideration was taken that both transverse indentation and tensile tests were performed under strains consistent with shortening and largely in the linear regime of myocyte mechanical properties, i.e., a myocyte in the SL range of 1.8–2.1μm. When derived from data acquired via myocyte tensile tests, the computational model (Fig. 5 D) exhibits an overshoot of relaxation that is not observed in any experiments of myocyte shortening. This is likely an artifact that may arise from nonlinear effects or the incorporation of myofilament resting tension as a series elastic element that does not provide restoring force in a relaxing cell. Overall, we feel the main finding of this work—that MT-dependent viscosity impedes the motion of RCMs—is strongly supported by the results; however, caution should be taken in extending this finding to different mechanical conditions such as significant preload or afterload or at different shortening rates and amplitudes.

Although this study aimed to characterize the MT contribution to mechanics at the single-myocyte level, myocyte behavior is likely to be significantly influenced by the complex interconnected environment of myocytes, nonmyocytes, and extracellular matrix that must all deform in a functioning myocardium. Thus, tissue-level examinations, although likely more complicated, are a clear next step. Further, the cell stretch technique used here relies heavily upon adhesion to the cell membrane of an aligned myocyte and may sense both shear resistance and axial tension. Tissue studies using papillary muscle or trabecula could preferably isolate axial tension in a context in which myocytes are in their native orientation. Previous myocardial strip experiments demonstrate a VE contribution of MTs at the tissue level (38), but these results must be expanded to determine the role of MT-dTyr.

In summary, depolymerization or tyrosination of MTs enhances myocyte contractility and contractile kinetics independent of changes in calcium handling. Transverse indentation and axial stretch independently show that MTs contribute to myocyte viscoelasticity by a mechanism that is dependent on post-translational dTyr. At slow strain rates, the steady-state stiffness of isolated rat myocytes is not significantly dependent on the MT network, but a progressive contribution to stiffness emerges as the strain rate of the mechanical test is increased. At deformation rates consistent with cardiomyocyte contractility, myocytes treated with colchicine or PTL are significantly softer, providing a mechanical basis for the increased contractility. Computational dissection of the VE influence on contractility indicates that the contractile phenotype observed with MT depolymerization or tyrosination can be explained by changes in myocyte viscoelasticity. In sum, the findings indicate that MTs act as cytoskeletal shock absorbers that mechanically regulate the amplitude and timescale of myocyte contraction by resisting rapid length changes during both systole and diastole.

Author Contributions

M.A.C. contributed to the design of the study, acquisition and analysis of the data, and preparation of the manuscript. C.Y.C and A.K.S. contributed to the acquisition and analysis of the data and preparation of the manuscript. K.B.M. contributed to the experimental design and preparation of the manuscript. B.L.P contributed to the experimental design, analysis of the data, and preparation of the manuscript.

Editor: Cynthia Reinhart-King.