Conformational entropy of a single peptide controlled under force governs protease recognition and catalysis

Significance

In the cell, enzymes such as proteases target peptides with specific amino acid sequences. The mechanism of specificity is typically examined by looking at the peptide structure in complex with the enzyme. However, a question remains: How do enzymes recognize a free peptide that can adopt a large number of geometries before the association? Here, we propose a method to control the peptide flexibility by stretching it under force. In our assay, we can follow the substrate elongation and its catalytic cleavage by a single protease. Finally, we designed a computational model to describe all possible geometries of a free peptide that acts as an elastic under force and assessed the impact of peptide flexibility upon the specific recognition.

Abstract

An immense repertoire of protein chemical modifications catalyzed by enzymes is available as proteomics data. Quantifying the impact of the conformational dynamics of the modified peptide remains challenging to understand the decisive kinetics and amino acid sequence specificity of these enzymatic reactions in vivo, because the target peptide must be disordered to accommodate the specific enzyme-binding site. Here, we were able to control the conformation of a single-molecule peptide chain by applying mechanical force to activate and monitor its specific cleavage by a model protease. We found that the conformational entropy impacts the reaction in two distinct ways. First, the flexibility and accessibility of the substrate peptide greatly increase upon mechanical unfolding. Second, the conformational sampling of the disordered peptide drives the specific recognition, revealing force-dependent reaction kinetics. These results support a mechanism of peptide recognition based on conformational selection from an ensemble that we were able to quantify with a torsional free-energy model. Our approach can be used to predict how entropy affects site-specific modifications of proteins and prompts conformational and mechanical selectivity.

Chemical modifications affect the majority of proteins after translation, modulating their functions and fate in the cell (1). These reactions are predominantly catalyzed by specific enzymes that recognize target sequences in proteins. Efforts in the field of proteomics and system biology to map these modifications, to characterize the enzyme specificity, and to assess the reaction rates are critical for a comprehensive understanding of cellular functions.

For the chemical modification to occur, it is critical that the enzyme can access the targeted substrate (2). In this regard, sequence specificity is key and is typically deduced from the static structure of an enzyme:substrate complex, which shows how the peptide substrate occupies the binding site where residues adopt a precise orientation (3, 4). In contrast, countless studies provide more sophisticated insights into conformational changes ranging from local reorganization of loops and side-chain residues to large domain rearrangements (5–9). Whereas most of these studies deal with the flexibility of the enzyme, computational approaches suggest a central contribution of the substrate flexibility (10). The experimental evaluation of substrate dynamics raises indeed the challenge of detecting kinetically distinct conformations in a large ensemble of short-lived states. In exceptional circumstances, binding to disordered peptide involves detectable conformational states (11). Even given its likely prominence across enzymatic reactions, the impact of the substrate dynamics, and, more precisely, the reduction of conformational entropy due to the binding remain vague.

If the peptide chain must be flexible to enter the binding site, two fundamental questions arise: What is the entropic penalty for attaining the bound conformation from the ensemble of free conformations and how can we monitor this substrate dynamic along the recognition event? We decided to manipulate the conformation of a single-molecule peptide substrate, modulated by stretching forces, in the context of a proteolytic reaction. Proteolysis is an irreversible posttranslational modification that causes either the maturation or degradation of proteins, playing a central role in cellular signaling and proteostasis (12, 13). Sequence specificity has been determined for a wide range of endoproteases that typically recognize proteolytic sites formed by consecutive residues flanking the scissile peptide bond (3). It is critical that proteases have a limited range of potential substrates to restrict promiscuous and deleterious off-target cleavage in the crowded cellular environment.

We developed an enzymatic assay, based on protein engineering and force spectroscopy, to stimulate and scrutinize rapid reaction kinetics from single events of peptide cleavage. Our findings unravel a fundamental contribution of conformational entropy implying that sequence specificity is responsible for conformational and mechanical selectivity that may govern the enzymatic modification of a myriad of proteins.

Results

Design of a Single-Molecule Enzymatic Assay.

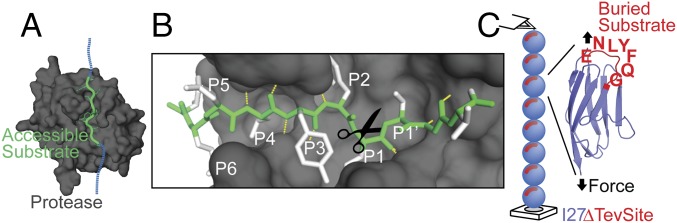
We engineered a substrate consisting of a polyprotein (I27∆TevSite)₈ that contains eight repeated I27 Ig domains from human titin (14–16). The known mechanical properties and stability of I27 are adequate for single-molecule manipulation (14). In each I27 domain, the engineered proteolytic site, TevSite, is recognized specifically by the cysteine protease Tev, from the Tobacco etch virus. The Tev protease, an enzyme extensively used to cleave tags in recombinant proteins, was selected for its high stability and solubility (17) and for its ability to recognize precisely the seven-residue-long amino acid sequence ENLYFQ↕G (Fig. 1A). The high specificity is essential to prevent promiscuous cleavage that may lead to intricate kinetics (18). In this optimal sequence, conventionally annotated P6-P5-P4-P3-P2-P1↕P1′, the scissile peptide is located between the residues P1 and P1′ (3), while P6–P1′ adopts a precise backbone curvature that dictates the orientation and accommodation of the residues in their specific pockets [Protein Data Bank (PDB) ID code 1LVB] (Fig. 1B) (19). For the success of our assay, the substrate engineering required the introduction of a P6–P1′ segment protected from degradation in the folded I27 without compromising the stability of the mutated substrate I27. With this concern, we replaced the unstructured loop S₂₆EPDVH₃₁ connecting β-strands B and C in the I27 domain (PDB ID code 1TIT) by the P6–P1 peptide ENLYFQ. Crucially, the native residue G₃₂ in position P1′ is engaged in β-strand C, suggesting restricted flexibility and accessibility to the enzyme (Fig. 1C). To verify the stability of (I27∆TevSite)₈ and its protection from cleavage, we first monitored in bulk the enzymatic efficiency in the absence of mechanical perturbation. A large excess of enzyme (1:5) indicated an exceptionally slow cleavage of I27∆TevSite (more than 1 h for completion), whereas the reaction was considerably faster for an accessible site (SI Appendix, Fig. S1). The limited proteolysis of I27∆TevSite in this stringent degradative condition suggests that the site is predominantly inaccessible, while the conformational dynamics of I27 leads to transient exposure to the TevSite. This observation implies that destabilization of I27 domain can favor the reaction. Thus, we proposed placing (I27∆TevSite)₈ under mechanical perturbation to accelerate and control the unfolding transition of the substrate stretched from its termini and to prompt the exposure of the TevSites (20).

Fig. 1.

Experimental framework. (A) Structure of the Tev protease (gray surface) bound to its substrate (green tube). The additional blue tube represents the contiguous extended chain. For clarity, residues F172 and K2201 are not shown on the surface. (B) P6–P1′ (green) accommodates in the binding-site cleft with a curved backbone geometry stabilized by hydrogen bonds (yellow dashes) orienting the side chains (white) toward the specific pocket. (C) With an atomic force microscope, we applied a stretching force (black arrows) to a single octamer of the Ig domain I27ΔTevSite. Each I27 folded domain (blue) contains a Tev cleavage site ENLYFQG (red). The structure of I27 (PDB ID code 1TIT) shows that the last residue of ENLYFQG corresponds to the native glycine G32 and participates in the β-strand C arrow colored in blue and red. It suggests that the Tev site is not accessible in the folded I27ΔTevSite domain.

Force Activates the Proteolytic Reaction.

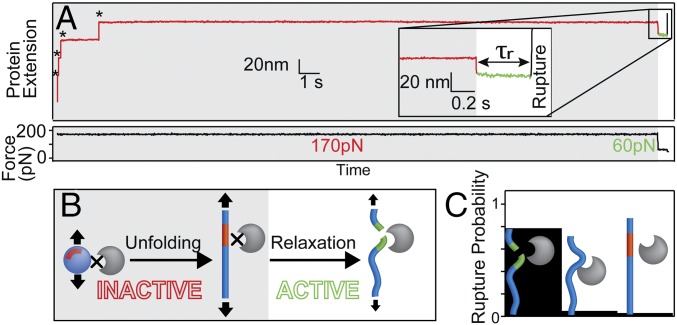
We used an atomic force microscope in a force-clamp mode to apply constant force pulses to single (I27∆TevSite)₈ molecules (21). At 170 pN, (I27∆TevSite)₈ stretches and produces experimental traces with a typical staircase in which steps mark the unfolding and stretching of individual I27∆TevSite domains. The expected length of the steps (25.2 ± 1.2 nm, n = 160) is used as a reference to select the recordings and to evaluate the number of unfolding domains in each trace (22). The time course of the unfolding events (unfolding rate of 4.42 ± 0.69 s⁻¹) confirms that the S₂₆EPDVH₃₁ mutation moderately impacts the mechanical stability of I27∆TevSite (SI Appendix, Fig. S2) (22, 23). With the addition of Tev (9 μM), we obtained similar traces, although the exposure and the extension of the scissile bond by force was expected to induce the proteolytic reaction immediately after the first unfolding events, as deduced for an accessible TevSite at zero force (SI Appendix, Fig. S1). Instead, the rupture probability of the tethered protein, marked by a loss of the applied force, was extremely low during a 30-s pulse, occurring in only 20% of traces (n = 69). Mechanical rupture of the protein backbone is unlikely at this range of force, suggesting that this occasional rupture occurs upon the detachment of the stretched polyprotein from the tip of the cantilever (24). We hypothesized that the mechanical strain at high force prevents the reaction from occurring; to test this, we inserted a second pulse to probe the reaction with a force three times lower (60 pN) after the inhibitory high force. The 170–60 pN transition induced a quick relaxation of the chain that reached a less-extended conformation. At 170 pN, the chain is stretched to 87% of maximum extension, while the chain relaxed to 78% at 60 pN (SI Appendix, Fig. S3). Remarkably, all traces display a quick rupture of the tethered protein after relaxation (Fig. 2A), contrasting with the slow detachment at high force. This two-pulse experiment strongly suggests that the cleavage is activated by the unfolding and subsequent relaxation of the extended protein at low force (Fig. 2B). We probed the reaction kinetics at millisecond resolution in the recordings by measuring the dwell time τ_r in the relaxed state delimited by two sharp events, the quick relaxation at 60 pN and the abrupt rupture of the signal. The average dwell time collected from several recordings is short (average τ_r = 1.70 s, n = 35), and 78% of traces displays a τ_r shorter than 1 s during the probe pulse (Fig. 2C). In contrast, this percentage drops to less than 5% for traces obtained at high force (170 pN) or in the absence of the cleavage site when unmutated I27 is stretched (SI Appendix, Fig. S4). This last control rules out artifactual short τ_r due to a noncatalytic effect of the enzyme or the existence of alternative cleavage sites in the unmutated I27. Finally, we optimized the force pulse protocol by reducing the first pulse to 3 s, a time sufficient for the complete unfolding of the poly I27∆TevSite substrate.

Fig. 2.

Mechanical activation of the proteolytic cleavage. (A) This experimental trace shows the protein extension marked by mechanical unfolding events of I27ΔTevSite domains (*) in presence of 9 μM Tev. The zoomed Inset shows the protein extension during the 170 pN–60 pN transition. Dwell time τ_r (in green) is defined by the abrupt events of chain relaxation and rupture at 60 pN. (B) Schematic of the enzymatic activation mechanism. The proteolytic site remains protected (gray background) from digestion in I27ΔTevSite folded or overstretched at 170 pN. The gain of flexibility acquired during the 170 pN–60 pN transition activates the catalysis. (C) The probability of rupture before 1 s for various experimental conditions [60 pN in the presence of Tev (Left), 60 pN in the absence of TevSite (Center), and 170 pN in the presence of Tev (Right)].

Reaction Kinetics Examined at the Single-Molecule Level.

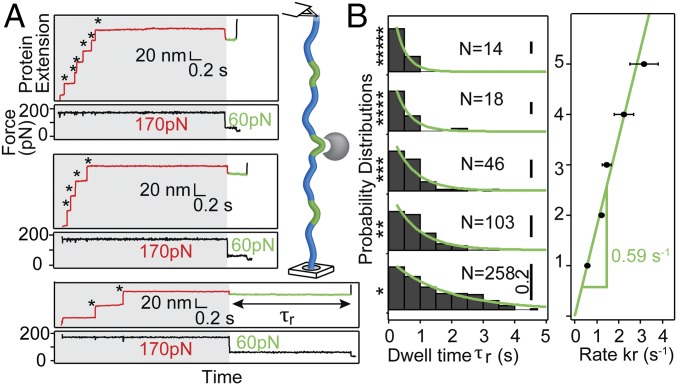
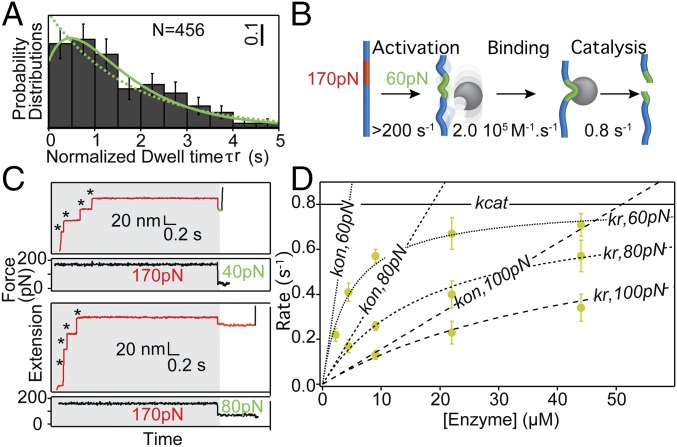
The (I27∆TevSite)₈ octamer contains one engineered scissile bond per domain so that the total number of unfolding events captured in the first pulse, which can vary from one to eight in our recordings, determines the extent of cleavable sites in the stretched protein. Indeed, a higher number of unfolding events correlates with shorter dwell times (Fig. 3A). To compare the rupture kinetics as a factor of accessible sites, we computed dwell-time histograms for different sets of traces classified by the number of unfolding events. The quasi-single exponential decay of dwell-time probability distribution at a first approximation implies a two-state transition (Fig. 3B). Strikingly, the overall reaction rate displays a strong linear dependence (Pearson’s coefficient = 0.98) with the number of sites (slope = 0.59 ± 0.02 s⁻¹, r² = 0.9) similar to the rate observed for traces with a single unfolding domain (0.57 ± 0.04 s⁻¹) (Fig. 3B). In a sharp contrast, the number of unfolding events does not influence the occasional detachment detected in the control experiments (SI Appendix, Fig. S5). The product of dwell times by the number of accessible site provides a normalized value of τ_r reporting the rupture time per site (Fig. 4A). Exponential fit to the normalized τ_r distribution (χ² = 13.2, P_0.05 = 0.83) (Fig. 4A, dashed green line) gives the foreseen reaction rate per site, k_r = 0.56 ± 0.06 s⁻¹. However, the normalization led to a larger dataset of dwell times (n = 456) with a distribution that fits best with a sigmoidal curve, inferring a kinetic intermediate in the reaction mechanism. This model of pre–steady-state kinetics conveys the reaction series (E+S → E S → E+P) where the intermediate complex E S, formed by the substrate S and enzyme E, is governed by the second-order rate k_on and the first-order catalytic rate k_cat (Fig. 4B). The modeled distribution, derived by Lu et al. (25) (SI Appendix, Eq. 2) improved the goodness of the fit to the experimental data (χ² = 7.9, P_0.05 = 0.99) (Fig. 4A, solid green line) with associated constants k_on (2.04 ± 0.75 × 10⁵ M⁻¹⋅s⁻¹) and k_cat (0.79 ± 0.05 s⁻¹). Monte Carlo bootstrapping methods confirmed the robustness in capturing these parameters from the dwell-time distribution (SI Appendix, Supplementary Materials and Methods). Nevertheless, this analytical solution from a single distribution requires a large dataset and can suffer from imprecision (26).

Fig. 3.

Cleavage kinetics measured at the single-molecule level. (A) Stretching (I27ΔTevSite)₈ in presence of enzyme (9 μM). Shown are examples of traces with six (******), four (****), and two (**) unfolding events. As represented in the schematic, the attaching points for each recording determine the number of unfolding domains and accessible cleavage sites. (B, Left) Distribution of dwell times, τ_r, for traces classified by the number of unfolding events. N indicates the number of traces. (Right) The rupture rate k_r is proportional to the number of unfolding events (correlation = 0.59 s⁻¹, r² = 0.9).

Fig. 4.

Kinetics of the formation of the protease:substrate complex depends on the applied force and enzyme concentration. (A) Fits to the distribution of normalized τ_r (60 pN, [Tev] = 9 μM) are based on a two-state model (k_S→P = 0.56 s⁻¹, solid green line or a three-state model (k_E+S→ES = k_on = 2.04 × 10⁵ M⁻¹·s⁻¹ and k_E:S→E+P = k_cat = 0.79 s⁻¹, dashed green line. Error bars are based on a bootstrap. (B) Schematic of the overall reaction kinetics suggested by the fit in A. (C) Recordings obtained with a probing force of 40 pN and 80 pN ([Tev] = 9 μM). (D) Reaction rates measured for different enzyme concentrations and forces.

To further verify this potential kinetic model, we repeated the experiments varying the concentration of enzymes present in solution and calculated the resultant rate k_r. In the low range of micromolar concentrations an increase in concentration shows a clear acceleration of the reaction, marked by shorter τ_r. This concentration dependence, presented in Fig. 4D, displays a hyperbolic curve where k_r reaches a plateau at a higher concentration, marking the rate-determining step, k_cat. Data were fitted to the single-molecule Michaelis–Menten equation (SI Appendix, Eq. 3) (27). The resulting k_cat (0.80 s⁻¹) coincides with the constant measured from a single distribution (Fig. 4A) and from bulk Michaelis–Menten assay at 0 force (28). We also confirmed the association rate (k_on = 1.78 × 10⁵ M⁻¹⋅s⁻¹) for a substrate extended at 60 pN. Moreover, it is worth noting that the binding of the ES complex also relies on its dissociation constant k_off, that we ignored here. Introduction of this additional term in our kinetic model showed that k_cat is significantly faster than k_off, probably because of the numerous hydrogen bonds and hydrophobic contacts stabilizing the ES interface (SI Appendix, Supplementary Materials and Methods and Fig. S6).

Remarkably, the rupture reaction modulated by the concentration of enzymes is also affected by the applied force, as revealed by the activation of the reaction upon the 170 pN-to-60 pN transition. We measured the reaction kinetics with adequate protocols based on a range of enzyme concentration and probing forces that permit measurable fast reactions. The observed dwell times, τ_r, increase when the probe force rises toward the inhibitory condition at 170 pN (Fig. 4C). Fits to the data reveal that the catalytic constant k_r is moderately affected by the force (k_{cat, 80 pN} = 0.75 s⁻¹, k_{cat, 100 pN} = 0.57 s⁻¹), while the on-rate displays a major contribution to the rupture rate (k_{on, 80 pN} = 4.31 × 10⁴ M⁻¹⋅s⁻¹ or k_{on, 100 pN} = 1.57 × 10⁴ M⁻¹⋅s⁻¹, for a fixed k_cat = 0.80 s⁻¹). In conclusion, from our single-molecule assay we can distinguish the contribution of the catalysis and the force-dependent binding of the enzyme to stretched conformations of the substrate.

Backbone Conformational Dynamics of Stretched Proteins.

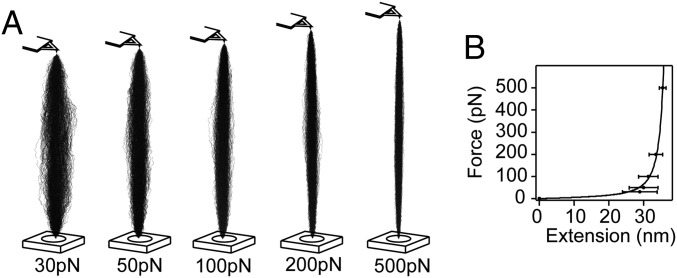
To clarify how the mechanical perturbation tunes the binding, we investigated the conformation of a stretched protein in response to force. In the last decades, polymer physics emerged to describe the elastic properties of semi-flexible chains under end-to-end pulling forces. In particular, the worm-like chain (WLC) model (29) is effective to fit stress–strain curves of stretched proteins (16, 30, 31) but remains inadequate to understand intricate enzymatic kinetics implicating a stretched substrate. In particular, we show that the moderate change of the end-to-end distance (11% of the contour length) observed when the force drops from 170 pN to 60 pN triggers a sharp transition, accelerating the association constant by several orders of magnitude. The atomistic details of the local deformation of the stretched chain, absent in the WLC model, provide alternative insights to elucidate force-dependent reactions (20). Therefore, we simulated a protein model consisting of a polyalanine made of 100 residues elongated upon force with steered molecular dynamics (SMD) (SI Appendix, SI Materials and Methods) (32). In the trajectories (Fig. 5A), the conformational space of the protein backbone is examined in relation to the two consecutive backbone dihedral angles, φ and ψ (33). Correlations between φ and ψ are visualized with 2D Ramachandran plots, revealing the favorable geometries. We retrieved typical WLC parameters modeling the force–extension relationship and observed a loss of backbone fluctuations upon stretching that we can estimate from the trajectory (Fig. 5B and SI Appendix, Fig. S7) (33). Interestingly, the propensity to bend along the pulled chain is independent of the distance to the attachment points. All (φ,ψ) are equivalent, confirming that the torsional strain is in equilibrium in the stretched chain (SI Appendix, Fig. S8). This observation correlates with the experimental evidence that k_r is not affected by the number of the unraveling sites or the length of the pulled substrate. This suggests that the mechanical perturbation modulates the ability to visit a competent conformation of the backbone for the binding to occur. However, the verification of this hypothesis with SMD requires longer simulations to mimic our experimental observations that are captured in a millisecond timescale. Indeed, the description of the conformational dynamics from nanoseconds simulations remains incomplete because of the high barriers separating basins in the Ramachandran space.

Fig. 5.

Flexibility and extension of a protein probed with SMD. (A) Ensembles of 100-alanine conformations along the SMD trajectories. Backbones are represented as thin back lines, and the terminal ends are superimposed. (B) Extension of the alanine chain during the simulation. The fitting curve corresponds to the WLC model (p = 0.36 nm).

Estimation of the Conformational Entropy for a Protein Under Mechanical Perturbation.

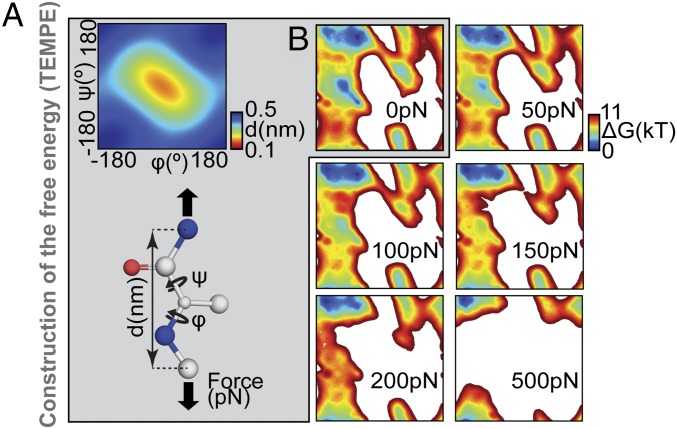
We propose an alternative approach to estimate more accurately how the backbone torsional free energy evolves under mechanical perturbation (Fig. 6). First, we computed the free energy, ΔG_0pN(φ,ψ), along the two dihedral coordinates of a model alanine peptide in explicit solvent using an enhanced sampling approach (34). In parallel, we calculated the extension d(φ,ψ) (in nanometers) of one amino acid for each (φ,ψ) couple (Fig. 6A). With the free-energy map and distance maps, we were in position to estimate the effect of force on the local curvature through a torsional free-energy model of protein elasticity, that we named “TEMPE.” At a given force, the free energy, ΔG(φ,ψ,F), was then obtained as: ΔG(φ,ψ,F) = ΔG_0pN(φ,ψ) − F⋅d(φ,ψ). The resulting maps obtained with TEMPE (Fig. 6B) are comparable to the ones obtained with SMD simulations but provide a more accurate description of the energy landscape, particularly for unstable or hardly accessible states (SI Appendix, Fig. S9). The TEMPE approach adequately estimates the complex convergence of the torsion angles to a confined region of the Ramachandran plot which corresponds to a straight geometry under force (Movie S1).

Fig. 6.

Torsional free-energy model of protein elasticity (TEMPE). (A) Description of the method (gray box). (Inset) This map displays the measured distance d for all (φ,ψ) couples. (B) We obtained the free-energy map of the Ace-Ala-Nme molecule at 0 pN (Upper Left) from ABF calculations. From these two maps (distance and free-energy at 0 pN), we produced new maps representing the energy surface of proteins stretched at various forces. Here, we show examples for 50 pN, 100 pN, 150 pN, 200 pN, and 500 pN. Movie S1 depicts all maps in the 0–500 pN range.

Conformational Selection Explains the Force-Dependent Proteolytic Reaction.

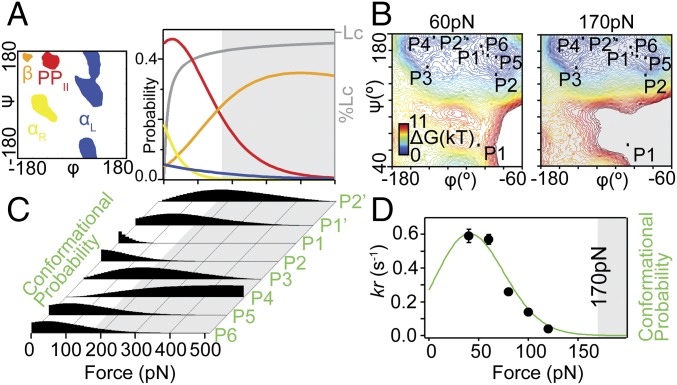
At any given force, we aimed to evaluate the propensity for the free substrate to visit the bound conformation observed in the holo structure of Tev (19). The substrate geometry was defined by eight (φ,ψ) couples corresponding to the substrate segment stabilized from P6 to P2′ by a total of nine backbone−backbone hydrogen bonds with the enzyme (SI Appendix, Table S2). It is noteworthy that the P2′ residue does not contribute to the specificity but its backbone forms a hydrogen bond with the enzyme. The resulting backbone geometry appears mostly straight in the binding cleft except for the curved scissile bond P1–P1′ that shows a distorted geometry of high energy that was not observed in the SMD trajectories. In Fig. 7A, the basins in the Ramachandran space show large rearrangements of their contour and depth in a narrow range of piconewton forces. For instance, the straightest geometry (β-strand basin) is more favorable than the α_R basin at forces higher than 41 pN and is more favorable than the PP_II basin at forces higher than 159 pN. The probabilities of visiting the PP_II and β basins are maximum at 24 pN (P_PPII = 0.47) and 399 pN (P_β = 0.35), respectively. Similarly, the eight (φ,ψ) coordinates of P6–P2′ display distinctive force dependencies. We considered a binding model based on a conformer selection model and thereby estimated the probability of visiting the full P6–P2′ conformation with 1°-resolution as the product of the eight uncoupled residue probabilities (Fig. 7 B and C and SI Appendix, Fig. S10A). The resulting probability is nonmonotonous and marks an optimal peak at 41 pN, illustrating the intricate influence of force on the substrate flexibility. This curve describes the ability of the substrate P6–P2′ to attain the competent conformation for binding and shows a very high correlation (Pearson coefficient r = 0.99) with the force-dependent kinetics measured experimentally (Fig. 7D and SI Appendix, Table S3). Our results emphasize the need to consider all states of the shallow energy surface describing extended proteins to explain the reaction kinetics (SI Appendix, Fig. S10B).

Fig. 7.

Force-dependent conformational entropy of the substrate affects its probability of visiting the bound conformation. (A) The probability of visiting the energetically favorable regions (α_R, PP_II, β, and α_L) of the backbone dihedral angles (φ,ψ) under mechanical perturbation (0–500 pN). These probabilities obtained from the TEMPE approach show large interchanges upon variations in the percentage of contour length Lc (p = 0.36 nm, WLC). (B) The backbone conformation of each amino acid in the bound substrate P6–P2′ is reported on the free-energy surface. In particular, the residue P1 displays a kinked backbone geometry (Fig. 1A) associated with a large increase in energy from 60 pN to 170 pN. (C) Normalized conformational probabilities for each P6–P2′ amino acid. (D) Correlation between the measured rupture rate k_r (black circles show data at 60, 80, and 100 pN reproduced from Fig. 4D) and the probability that P6–P2′ will visit its bound conformation calculated from TEMPE (green line).

Conclusion

In our single-molecule enzymatic assay, we induce conformations of a specific substrate with force to monitor the fast kinetics of its digestion by proteases present in solution. Force emerges as an adequate approach to initiate the reaction upon the unfolding and the quick relaxation of the substrate. The rapid transition from a rigid extended state to a relaxed cleavable state is essential to mark the beginning of the reaction. Dwell times are also defined by the final decrease in the tension that we expect to occur quickly after the reaction. Indeed, the C-terminal product P1′–P2′ shares only a weak interface with the enzyme that is probably short-lived under the applied force. Finally, the reaction must be fast so that the detachment rate is neglected compared with k_r, limiting the ambiguity between the two competitive mechanisms. The rapid rupture kinetics was enhanced and regulated by three factors: a high concentration of enzymes, the presence of multiple sites in the stretched substrate, and adequate forces that trigger compatible substrate conformations. The abrupt mechanical activation also allows pre–steady-state kinetics and prevents the saturation of the convolved enzyme by the substrate or the product, which often contributes to the overall kinetics measured in bulk. Our results unravel the contribution of the substrate dynamics upon binding (11, 35) and allow the direct determination of the catalytic rate. In addition, the force governs the internal conformational flexibility of the substrate while the enzyme is unaffected, a circumstance that permits new experiments in conditions that affect only the enzyme dynamics (e.g., denaturating agents in solution).

Our data support the notion that conformation selection rather than an induced-fit mechanism governs the substrate recognition. We quantified the entropic contribution upon substrate binding due to the shift from a large ensemble of preexisting conformations to a higher-energy conformation. Similar conclusions have been reached by NMR studies (36) and simulations (9, 37). The force-dependency profile in Fig. 7D suggests a maximum efficiency at a particular force (∼40 pN). Below this force, the large spectrum of accessible states slows the association, and above the optimal force the probability of visiting a compatible conformation drops abruptly. At higher forces, the loss of substrate flexibility slows the association via an entropic penalty. For instance, with the TEMPE approach we predicted that the penalty due to conformational entropy for visiting the bound conformation drops from 2.43 kT (1.44 kcal⋅mol⁻¹) to 0.07 kT (0.04 kcal⋅mol⁻¹) upon the 170 pN–60 pN transition (SI Appendix, Fig. S10C). The optimal force is therefore protein dependent and can be predicted for other posttranslational modifications from the ES structure using our TEMPE approach. Nevertheless, our force-dependent model of association does not exclude the possibility that the substrate first binds partially with a suboptimal conformation and then through a multistep mechanism.

The magnitude of the mechanical strain on a polymer is commonly expressed as a single coordinate, the end-to-end distance. Simple energetic models also provide insights into polymer elasticity, describing the internal friction with transitions between interconverting states (33, 38). Our statistical approach of protein elasticity, TEMPE, elaborates on the torsional strain represented by an ensemble of (φ,ψ) dihedral angles linked to the global conformational entropy of the cleavage site. Mechanical perturbation gradually turns the multiple shallow-basin energy landscape, which allows quick transitions, into a single deep funnel corresponding to an overstretched conformation. This energetic model correlates the entropic springwise elasticity of proteins showing good agreement with the SMD simulations and experimental kinetics. Therefore, TEMPE offers a generic model for better understanding the mechanics and mechanochemistry of proteins. However, its validity is probably limited to the piconewton range of force (∼40–500 pN) in which the elasticity is governed by the entropy of the chain. Indeed, this approach disregards the side-chain interactions at lower force, the integrity of bond distances and valence angles at higher force, and the impact of residues with unusual backbone geometries (i.e., proline and glycine) (33).

Our findings also suggest a physiological relevance in protein–protein association and biomechanics. Enzyme kinetics change with factors such as temperature or substrate sequence, but the elusive impact of mechanical perturbations remains intriguing. For instance, the well-documented catch bond illustrates how pulling forces can disfavor the dissociation of molecules under load. Here, we depict another mechanical regulation whereby the protein association is controlled by an end-to-end pulling force, a physiological perturbation common to a large variety of tensile proteins. Remarkably, the elasticity of the giant sarcomeric titin operates through large stretches of peptides prone to enzymatic mechano-dependent posttranslational modifications (20, 39, 40). Moreover, studies report that proteases cleave stretched proteins sensing a mechanical load (41, 42). In particular, hemostasis relies on the mechanically induced digestion of von Willebrand factor by the ADAM protease A2. Force-dependent proteolysis under the blood stream can be regulated by the mechanism presented in this study (43). It is also tempting to expand this phenomenon to the large catalog of mechanically stressed proteins, in particular protease activated receptors, adhesive proteins, or, in a force-independent manner, unstructured peptide in folded or intrinsically disordered proteins.

From an evolutionary perspective it is possible that enzymes responsible for posttranslational modifications diverging from the perfect enzyme evolved to recognize their substrate with adequate kinetics and substrate promiscuity in response to the dynamic nature of targeted proteins. Similarly, the conformational entropy of the substrate, which can be either transiently or intrinsically disordered in vivo, may affect the recognition by cold- or heat-adapted enzymes.

Materials and Methods

Force Spectroscopy Experiments.

We obtained the (I27ΔTevSite)₈ octamer protein following a standard protocol to produce the recombinant cDNA of tandem-repeat constructs engineered from the synthetic gene I27ΔTevSite (14). Details of protein sample preparation are presented in SI Appendix.

All experiments were performed with EB buffer [150 mM Hepes (pH 7.2), 150 mM NaCl, 10 mM EDTA]. We deposed ∼2–5 μL of newly filtered (I27ΔTevSite)₈ sample on a gold-coated coverslip mounted on a piezoelectric positioner. We mounted a triangular silicon nitride cantilever (MLCT; Bruker) on a fluid cell and covered it with ∼30 μL diluted and filtered Tev solution with the addition of 0.1 mM Tris(2-carboxyethyl)phosphine (TCEP) (from fresh-frozen aliquots packaged in argon to avoid oxidation) to ensure a full enzymatic activity. We positioned the fluid cell on the coverslip after partial evaporation (1–3 min) of the (I27ΔTevSite)₈ sample. All single-molecule experiments were carried out with an atomic force spectroscope (Luigs–Neumann) that uses a proportional integral derivative (PID) feedback system to set the applied force. We evaluated the spring constant of each cantilever (∼14–17 pN⋅nm⁻¹) using the equipartition theorem (44). All details about the data analysis, fits, and kinetics are presented in SI Appendix.

Implementation of the TEMPE Approach.

To compute the free-energy landscape along the backbone dihedral angles (φ, ψ), we used a simple model consisting of the Ace-Ala-Nme molecule (often incorrectly referred to as “di-alanine”) solvated in a cubic water box (2.4 nm³) using the simulation protocol and force fields described in SI Appendix. The zero-force potential of mean force along the (φ, ψ) angles of the central residue was determined using the adaptive biasing force (ABF) method (45) to obtain a map of the discrete torsional free-energy space of the backbone ΔG_0pN(φ,ψ) with a resolution of 1°, which was observed to be similar to previous calculations (46). We implemented a PyMOL script to generate the distance-angle map d(φ, ψ) with the same 360 × 360 dimensions by measuring for an amino acid i the distance C_i−1 − N_i+1 for each possible (φ, ψ) with 1° increments. In this calculation, bond lengths and valence angles were kept constant, and (φ, ψ) combinations forbidden because of steric hindrances were not considered. Tilted Ramachandran maps of the free energy for various forces, F, were computed with Python2.7 (Numpy1.11 Library) by subtracting from the zero-force potential mean force (PMF) the term −F*d(φ, ψ), with the constant F in piconewtons and d in nanometers. Implementation of SMD simulations is presented in SI Appendix, Supplementary Materials and Methods.