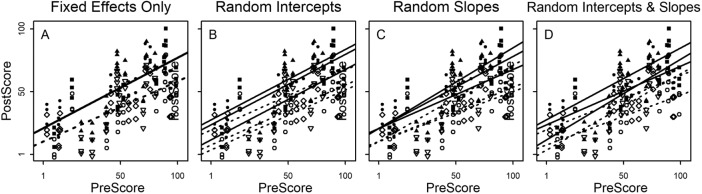
FIGURE 5.

Depending on the structure of the data, a fixed effects–only model (A) may not be the best model. There are three main ways to specify random effects in multilevel models: (B) as random intercepts, in which the slope is the same for all groups, but the intercepts vary for each group; (C) as random slopes, in which the intercept is the same for all groups, but the slopes vary for each group; and (D) as random intercepts and random slopes, in which all groups are allowed to have different slopes and different intercepts. Illustrated here, students (points) are nested in six sections (illustrated by the six combinations of filled/unfilled symbols in different shapes). There are two treatments, illustrated by filled and unfilled symbols. The lines show how each approach models the relationship between PreScore and PostScore. In a fixed effects–only model (A), a single regression line is fit for the treatment (filled) and control (unfilled symbol), ignoring sections; in a random effects model (B–D), separate regression lines are fit for each section. In the random intercepts model (B), the intercepts are allowed to vary by section but not the slopes (thus, the lines are parallel); in the random slopes model (C), the slopes are allowed to vary for each section, but not the intercepts (thus, all the lines start at the same place); and in the random intercepts and random slopes model (D), both the intercepts and the slopes are allowed to vary for each section. The overall model fit in B–D is essentially the weighted average of the regression lines for each group and is not shown.