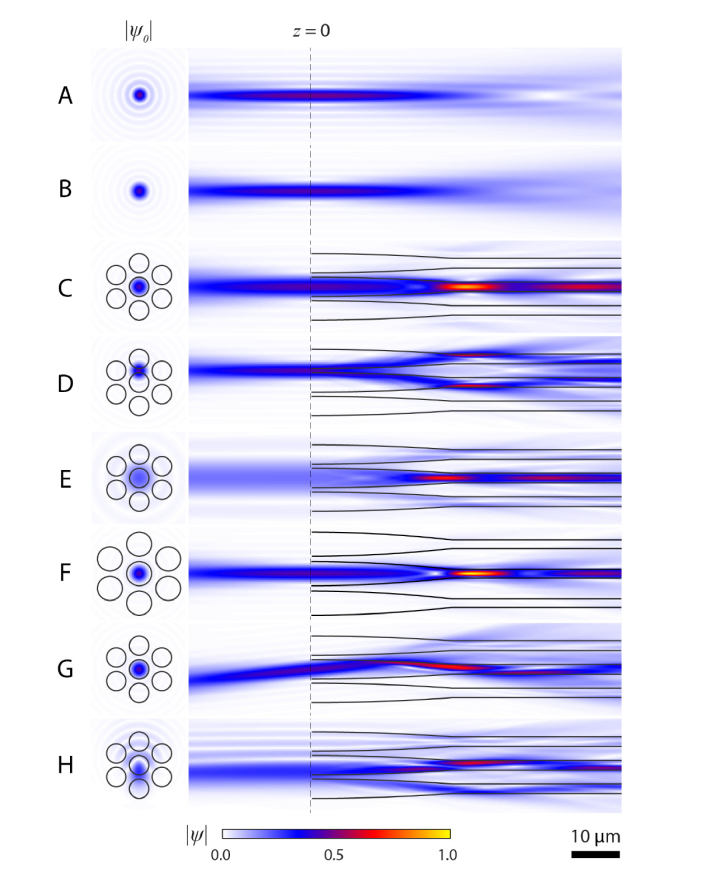
Fig. 3.

Examples of light propagation in cone photoreceptors. Propagation in water (n = 1.33) using a uniform field at the pupil (A) or with a truncated Gaussian (B). When light is incident centrally on a photoreceptor (C) beating of the field is evident in the outer segment. (D) Propagation when beam lands between photoreceptors (shifted 0.61d₀). (E) Diminished light intensity occurs when the beam size is set to 2.0 mm. (F) Propagation down larger photoreceptors (d₀ = 5 μm) leads to the largest peak intensity in these examples. (G) Propagation with light entering at an angle of 7.5°. (H) Example with a Zernike coefficient corresponding to coma of 0.1 μm. Modulus of the electric field for the initial fields (right) and the fields in the x-z plane for x-polarized light (left) are normalized to the peak electric field, which occurred in panel F. Light in the negative z direction was calculated by propagating the complex conjugate of ψ₀ through a refractive index of 1.33. For all examples, unless stated, beam diameter = 5.85 mm, 1/e width of Gaussian = 4.75 mm, λ = 543 nm, d₀ = 4 μm, d_os = 1.75 μm, dx = dy = 0.1 μm, dz = 0.2 μm. Values for refractive index and lengths of segments are given in the Methods.