Biophysical investigation of living monocytes in flow by collaborative coherent imaging techniques

Abstract

We implemented a completely label-free biophysical (morphometric and optical) property characterization of living monocytes in flow, using measurements obtained from two coherent imaging techniques: a pure light scattering approach to obtain an optical signature (OS) of cells, and a digital holography (DH) approach to achieve optical cell reconstructions in flow. A precise 3D cell alignment platform, taking advantage of viscoelastic fluid properties and microfluidic channel geometry, was used to investigate the OS of cells to achieve their refractive index, ratio of the nucleus over cytoplasm, and overall cell dimension. Further quantitative phase-contrast reconstructions by DH were employed to calculate surface area, dry mass, and biovolume of monocytes by using the OS outcomes as input parameters. The results show significantly different biophysical cell properties, confirming the possibility to differentiate monocytes from other cell classes in flow, thus avoiding chemical cell staining or labeling, which are nowadays used.

1. Introduction

The human blood cell pool is divided into two main classes, the so-called erythrocytes (or red blood cells) and the white blood cells (WBC). Erythrocytes represent 99.9% of blood stream cells and can be assumed to be biconcave shaped and deformable cells with no nucleus, fulfilling the task of carrying vital gases in and out from every tissue of the body [1]. On the other hand, WBCs are a complex, heterogeneous and widespread group of cells, which are responsible for the maintenance of the body health [2]. Moreover, WBCs can be distinguished in cells with or without granules. Neutrophils, basophils and eosinophils belong to the cells with granules, while lymphocytes and monocytes are composed without [3].

The screening of morphometric cell properties (shape and inner structure) has recently shown to give important information to distinguish fractions of cell classes and/or states, especially when dealing with sparsely present cells [4–8]. Additionally, in case of disease, a significant change of cell morphology can occur, which require a fast and complete morphometric single cell screening with the final goal to identify pathologic from physiological cells [9]. For instance, the changes of the relative monocyte amount in the peripheral human blood, lower or higher than physiologic one, as well as anomalous cell shapes or cytoplasm complexity can be indicative for dysregulated responses to inflammation stimuli [10,11]. This is evident when dealing with chronic inflammations, which can be related to serious systemic pathology [12,13]. Moreover, it is well known that in the case of tumoral monocyte diseases (such as leukemia), significant morphometric and optical cell modifications occur [14]. However, physiological monocytes are sparsely present in peripheral blood, and noticeably favor to adhere and aggregate compared to other WBCs, making their single cell investigation challenging [15]. Therefore, a great number of biophysical monocyte properties -using more than one coherent imaging tool- would substantially enhance the identification of specific cell states.

Over the past two decades, a lot of research groups provided novel and accurate strategies to investigate cells, considering either camera-based flow cytometry system [4–8] or technologies using 3D label-free quantitative phase imaging (QPI) [16–21]. In general, such approaches have both in common a high-throughput modality [19–23] and the possibility to analyze cells in their physiological conditions using microfluidic systems [4–7,24–26]. Recently, an innovative microfluidic device, able to provide a viscoelastic 3D particle alignment and coherent imaging, has been demonstrated for polystyrene microspheres [27] and blood samples [28–31]. In particular, as shown in Ref. 28, a simple and fast method to obtain biophysical properties of individual living peripheral blood mononuclear cells (PBMC, i.e. lymphocytes and monocytes) in a microfluidic based measurement system has been demonstrated. In these experiments, the amount of some cells showing a dimensional range fitting with monocytes were observed. However, the throughput of investigations guaranteed the analysis of few hundreds of PBMC, making a statistical monocyte characterization challenging. Therefore, a robust investigation of monocytes is still needed, considering their low amount in (potentially) a million blood cells.

In this paper, we report a straightforward label-free way to characterize monocytes in flow, using the joint action of optical signature (OS) recognition by pure light scattering [27–32] and digital holography (DH) in microscopy [25,26,33–35]. In particular, OS of 3D viscoelastic aligned individual cells were acquired by scattering measurements, and QPI reconstructions by DH were used to track cells in flow and further investigate them along a microfluidic channel, allowing the full morphometric characterization of monocytes. The OS of living cells were investigated using an adequate simulation model, based on a coated-sphere with different biophysical cell properties such as cell dimension (d_c), refractive index (n) and ratio of nucleus over cytoplasm (n/c-ratio). Direct matching of experimental results with simulation data were used to obtain an efficient detection of individual living cells and further used as input parameters for DH investigations. In fact, the holographic 3D tracking framework [36,37] was used to investigate the precise axial position of a single cell in the viscoelastic microfluidic flow and to calculate further biophysical cell properties such as the surface area (S), ellipticity (E), biovolume (V) and dry mass (DM). The joint combination of both coherent imaging techniques allowed to label-free investigate single living monocytes in flow at high accuracy.

2. Materials and methods

2.1 Samples preparation

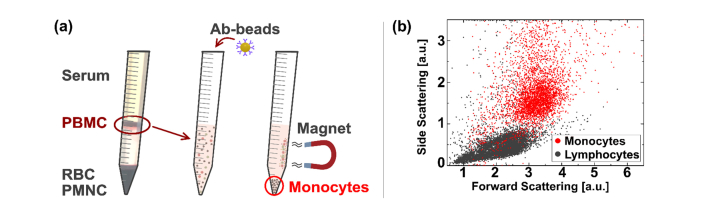
For monocyte measurements in their native conditions, 30mL of peripheral human blood were taken from a healthy male donor by standard venipuncture procedure and stored in K₂EDTA tubes (BD, VACUTAINER) to avoid possible physiological coagulation phenomena. The sample was taken after obtaining informed consent from the donor in accordance with the relevant guidelines and regulations. Within 30 min after the donation, the blood volume was treated for cell extraction with a density gradient polymer separation approach. Afterwards, the blood volume was diluted 1:1 with phosphate-buffered saline (PBS, EUROCOLNE) and laid on an equal volume of a certain density medium (Ficoll, SIGMA-ALDRICH) in standard 50mL plastic tubes. Afterwards, the sample was centrifuged at 250 $\overrightarrow{g}$ for 30 min without using the machine brake. Subsequently, the resulting PBMC ring was collected using a standard pasteur pipette and washed twice with RBC lysis solution to eliminate possible erythrocyte contaminations of the sample. As a next step, monocytes were isolated by a negative selection procedure with specific Ab-coupled magnetic beads (Dynabeads Untouched kit, INVITROGEN) and suspended in a viscoelastic 3-D alignment solution, consisting of polyethylene oxide (PEO − M_w = 4 MDa, SIGMA-ALDRICH) diluted in PBS. Figure 1(a) illustrate the cell class separation procedure.

Fig. 1.

Monocyte isolation procedure and flow cytometer measurement. (a) The three-step isolation procedure of monocytes from whole blood is illustrated. At the first step a gradient separation with ‘Ficoll’ was performed. The obtained PBMC ring is taken and suspended in PBS. Magnetic Ab-beads are added in the second step. Afterwards in the third step a magnet retains the bound content to the falcon tube surface, while monocytes remain free in the suspension to analyze. (b) Flow cytometer control of isolated monocytes (red) and added lymphocytes (gray), where two distinct zones are noticed. Monocytes show significant bigger forward and side scattering intensity values compared to lymphocytes.

We analyzed the isolation accuracy of monocytes (CD14-PE) versus lymphocytes (CD3-FITC & CD19-FITC) using a commercial flow cytometer (CyFlow SPACE, SYSMEX-PARTEC), where more than 94% of monocytes were positively detected by Ab-labeling (data not shown). Also, it can be seen from the scattering plot in Fig. 1(b), that monocytes (red) show significantly bigger forward and side scattering intensity values compared to lymphocytes (gray).

Before the experiment, cells were observed with a standard bright-field microscope (100× oil immersion objective, X81, OLYMPUS) to ensure the vitality and the maintaining of the physiological state of the cells in the viscoelastic measurement solution, see Fig. 2(a). Moreover, cell vitality was tested before (Fig. 2(b)) and after each measurement (Fig. 2(c)), using a standard ‘Trypan blue test’ approach (20 × objective, BX53, OLYMPUS), showing satisfying results. Furthermore, a portion of monocytes has been fixed in 4% paraformaldehyde and subsequently the nucleus was stained with ‘Sytox Green’ (THERMOFISHER), while the cytoplasm membrane was stained with ‘Wheat Germ Agglutinin’ (THERMO SCIENTIFIC, alexa fluor 488 conjugated). A z-stack of such a monocyte was acquired with a standard confocal microscope (LSM 710, ZEISS) and reconstructed in ImageJ to generate a 3D (Fig. 2(d)) and a single section (Fig. 2(e)) image, showing the typical monocyte shape and height of the nucleus as well as cytoplasm.

Fig. 2.

Monocyte observations. (a) Bright-field observation with 100× oil immersion objective of monocytes in 0.2g dL⁻¹ PEO-PBS. Trypan blue investigations with a 20x objective in color before (b) and after (c) cell measurements. (d) 3D reconstruction of confocal fluorescent z-stack images (ImageJ: plugin/Stacks - Z-functions/360- 3D project... Macro). (e) Confocal image of one slide of the fluorescent z-stack. (Green color shows the ‘Wheat germ Agglutinin’, while red color indicates the ‘Sytox Green’)

2.2 Experimental setups and methods

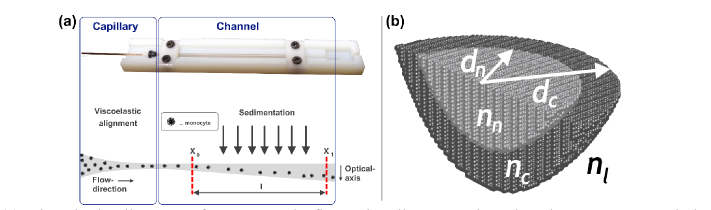
We designed a microfluidic device, where precise 3D-cell alignment takes place in a round shaped capillary (radius r_c = 25µm), mainly induced by a pressure driven viscoelastic polymer (PEO) and the capillary geometry, before cells are forced to pass into a highly transparent squared shaped measurement channel having a wider cross section of 500x500 µm. The measurement channel is fully sealed by a soft ferrule, through which the alignment capillary can simply pass into the squared channel. The other end of the alignment capillary is immersed in the cell sample. In fact, by applying a certain pressure on the sample, cells are constantly pushed through the whole microfluidic system, changing the viscoelastic forces of the medium and cell velocities according to the different cross sections of capillary and measurement channel. Notice that the centerlines of capillary and channel are collinearly placed, and no cell deformation was observed in the measurement channel.

However, we took advantage of viscoelastic cell migration effects in a capillary to align cells before investigating them in a subsequent square shaped channel. The alignment probability to the centerline of the capillary can be expressed by an adimensional parameter θ, which can be written as [38]

$$\theta =\widehat{\dot{\text{γ}}}{\text{λ}}_{\mathrm{t}}+{\text{β}}^2\left(L/r_c\right),$$ (1)

with a relaxation time λ_t = 0.123ms of the viscoelastic polymer (PEO of 0.2g dL⁻¹) and geometric parameters such as the confinement ratio β

$$\text{β}=d_c/2r_c.$$ (2)

Moreover, the capillary length L = 0.3m as much as the average shear rate $\hat{\dot{\gamma }}$ of the solution, ranging from 1154 to 2308s⁻¹ is relevant for the alignment probability, where $\hat{\dot{\gamma }}$ is defined as

$$\widehat{\dot{\text{γ}}}=\left(\text{Δ}{\text{Pr}}_c\right)/\left(4{\text{η}}_{0}L\right),$$ (3)

with ∆P (1500–3000 mbar) defining the applied pressure (generated by a P-pump, DOLOMITE) to push the sample through the capillary and ${\eta }_0$ = 0.0054Pa·s the zero-shear viscosity of the solution. In conclusion, a sufficient alignment condition exceeding θ≥1 can be simply achieved by an appropriate setting of all the previously mentioned parameters. At the end of the round shaped capillary a θ ranging from 16.7 until 33.4 was achieved for the mentioned ∆P range.

By contrast, for the much wider cross-section in the successive measurement channel, the β-ratio is not anymore fulfilled, by exceeding the defined maximal β value [38] of 10 and strongly reduced cell velocity from 0.18ms⁻¹ in the capillary to 0.000058ms⁻¹ at the channel (for ∆P = 1500mbar). In such a way, cells are less forced to stay on their track in flow and sedimentation gravity force can act on them, as shown in Fig. 3(a). This implies a stronger sedimentation influence for monocytes compared to other cell types, such as erythrocytes, according to their different biophysical properties.

Fig. 3.

(a) Viscoelastic alignment of monocytes in flow. The alignment takes place in a narrow round shaped capillary, before sedimentation forces can act in the aligned cells in wide squared shaped microfluidic channel. The entrance of the channel where scattering measurement have been performed is indicated by x₀, while 15 mm (l) downstream a second measurement position x₁ indicates the position, where DH observation have been performed. (b) Simulation model is illustrated; the indices n, c and l are used for nucleus, cytosol, and extracellular liquid, respectively. The nucleus is assumed to be in the center of the cell.

The scattering measurements has been investigated directly at the entrance of the measurement channel (x₀), where monocytes are assumed to be perfectly 3D-aligned and sedimentation effect is not relevant. On the contrary, DH observations have been performed after a distance l = 15mm in flow-direction (x₁), to investigate the axial position (z-direction) of investigated monocytes.

For OS investigations cell were simulated with a free available discrete dipole approximation (DDA v1.3b4) approach. Such a cell model approximates the scatterer by a lattice of dipoles, where the dipole number strongly depend on d_c, n and the numerical accuracy of the simulation itself. Hereby each individual dipole has an oscillating polarization in response to both the incident plane wave and the electric field [39]. However, the used cell model is based on a coated sphere, where the inner sphere is representing the nucleus of a cell and is assumed to be in the center of the overall model (see Fig. 3(b)). We used n-values of 1.33169 for the cell surrounding medium (n_l) and alternating values spanning from 1.36 to 1.48 for the nucleus (n_n) as well as the cytoplasm (n_c) of the cell, using a step size of 0.01. Only the real parts of the n-values were used for simulations, by considering that light absorption of the cell can be neglected. The n/c-ratio (nucleus dimension over full cell dimension) was alternated from 0.5 to 1.0 with a step size of 0.025 for best possible matching accuracy, while a wide range of d_c-values with a step size of 0.1µm was considered for un-polarized incident light.

We used a wide-angle (2-30°) static light scattering apparatus (λ = 633 nm), to obtain precise OS of monocytes in flow (Fig. 4(a)). The small angular resolution of 0.1022° allows us to distinguish morphometric cell characteristics within the sub-micrometric range, in a non-destructive and label-free way, at throughput rates up to 50 cells per second. In general, the incident light passes the microfluidic device from below, striking, one by one, target cells aligned in the centerline of the measurement channel. The OS of each individual cell is collected and mapped on the camera sensor by two lenses in series, while the incident light is blocked by a beam stop.

Fig. 4.

Schematic illustration of the OS- and DH-setup for monocyte investigations. (a) Illustration of the light scattering setup, where the incident light passes the microfluidic device from below, striking, one by one, monocytes aligned in the centerline of the measurement channel. The OS of each individual cell is collected and mapped on the camera sensor by two lenses in series, while the incident light is blocked by a beam stop. Moreover, the round shaped capillary for the cell alignment, the square shaped measurement channel as well as the ferrule which connect both microfluidic parts are indicated. The inset of LSP of a single monocyte is reported. (b) A sketch of the holographic setup is shown, where the incident light source is split into an object- and reference-beam by a beam-splitter. The object-beam strikes passing monocytes before both beams are simultaneously collected by the camera sensor. (c) Microfluidic device combined with the coherent imaging approach of OS (position x₀) and DH (position x₁) is shown.

DH measurements were performed with a classical off-axis arrangement in transmission mode (λ = 532 nm), with a 50 × long distance objective (Fig. 4(b)), such as reported elsewhere [25,26]. The light source is divided into an object beam and a reference-beam. The object-beam impinges on the sample before being collected by an objective and combined with the reference beam. QPI reconstructions can be used to measure biophysical properties of monocytes, thus, each optical axis position (see top-right inset in Fig. 4(b)), recovered for the cell tracking, is used to reconstruct the corresponding DH in the image plane. Then, we calculate the corresponding phase-contrast image. An example of such reconstructions is reported as the bottom-right inset in Fig. 4(b). Notice that, it would be possible to obtain numerically light scattering maps from QPI images. This approach is known as Fourier transform light scattering [40–42]. In order to do that, it is necessary, as first step to measure the scalar electric field at the image plane. Thus, as second step, it would be necessary to numerically propagate it to the far field using the Fourier transform, as demonstrated by in-line holographic measurements in a previous research [41,42]. However, we cannot employ efficiently this approach in our holographic measurements, since the flowing monocytes are located in different axial positions each other, thus hindering the recording in the image plane, as specified above. Moreover, the signal sampling, phase reconstruction, and unwrapping process are not robustly performed far from the image plane, where high-frequency interference patterns and phase discontinuities may occur [40]. For all experiments, bright-field microscope observations of the measured cells were taken before and after each experiment, showing a good preservation of the physiological monocyte state during the measurements without structural anomalies. As also reported in previous works [28–31], we can assume that during our short measurement times, the physiological cell state is not affected by the viscoelastic alignment solution, allowing non-invasive investigations of living cells.

3. Results and discussion

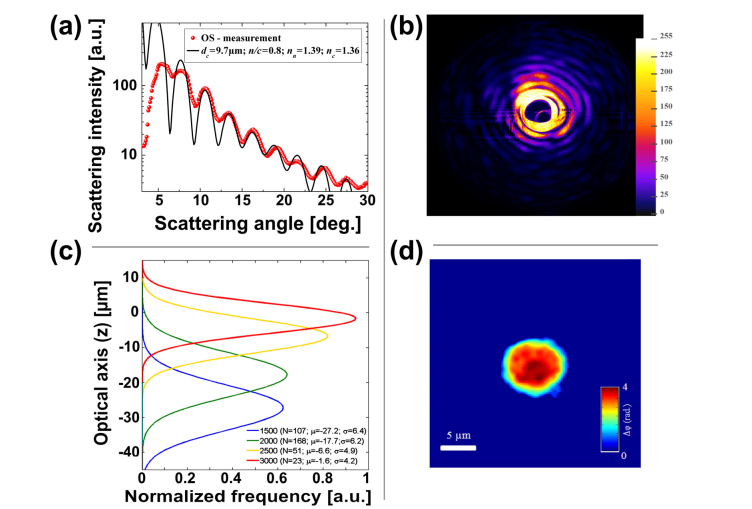
We tested our platform for 349 monocytes applying different flow rates. Cells were diluted in 0.2g dL⁻¹ of PEO-PBS to reach a final concentration of approximately 50 cells µl⁻¹. OS and DH measurements were jointly performed with sample volumes of about 100µL and an applied ∆P value of 2000 mbar for OS measurements and varying ∆P values for DH measurements (1500, 2000, 2500 and 3000 mbar). To investigate cells in flow via pure light scattering, we obtained OS of each investigated cell over the available scattering range to a continuous light scattering profile (LSP). Afterwards, we matched LSP outcomes with the best-fitting pre-calculated cell simulations to obtain individual biophysical cell properties. All obtained results were measured at a fixed channel position x₀, where stable 3D cell alignment was ensured. In Fig. 5(a) we report a typical monocyte outcome with the best matching simulation curve overlaid in black. Such LSP curve was calculated out of the OS image represented in Fig. 5(b). Hereby each concentric ring of high intensity values corresponds to an oscillation peak in the LSP of Fig. 5(a). More detailed information about the LSP calculation can be found elsewhere [27]. In Fig. 5(a), a reduced scattering intensity in the middle of the image can be noticed, due to the presence of the beam stop in the OS setup. Moreover, from 5° to 8° saturation effects are present, caused by the camera sensor, resulting in a significant matching discrepancy of experimental and simulated data. On the other hand, the discrepancies of the LSP minima between experimental and simulation data are due to physiological variances of the cell morphology, which the simulation model does not predict. Nevertheless, a good LSP matching using a coated-sphere simulation model was observed.

Fig. 5.

(a) LSP of monocyte measurement and overlaid simulation curve is shown. (b) The corresponding OS image recorded by the camera sensor is illustrated. (c) Optical axis results of monocytes investigated in measurement position x₁. An increased cell displacement from the initial optical axis position (z = 0) is observed for decreasing ∆P values and vice-versa. (d) Phase-contrast image of a typical monocyte investigated in flow is shown. The inset shows detected nucleus content.

From DH measurements we first investigated, cell positions in the optical axis direction at measurement point x₁, using the Tamura’s metric as holographic refocusing criterion [36]. Second, the quantitative phase map reconstruction of each focused monocyte (see Fig. 5(d)) was performed. Caused by the different cell velocities (∆P from 1500 to 3000mbar) and forces acting on monocytes in the alignment capillary and measurement channel, a selective cell displacement differentiation in flow was observed in x₁, as summarized in Fig. 5(c). Results indicated for decreasing cell velocity, higher optical axis shifts and vice-versa. Such results confirm previous PBMC investigations of our working group [28].

The proposed collaborative coherent imaging techniques permit to achieve the direct measurement of several biophysical properties of monocytes in flow. In particular, OS measures open up the possibility to directly achieve the cell dimension and the n/c-ratio of a passing cell assuming along with their total refractive index. Thereby all outcomes are retrieved from the unique simulation parameters used for the best matching simulation. Notice that the simulation curve database is made of more than 50 000 items. Cell matching results are reported in Table1. Beyond, the DH images measure the phase shift data Δφ, defined as [34]:

$$\text{Δφ}\left(x,y\right)=\frac{2\pi }{\text{λ}}\left[n\left(x,y\right)-n_l\right]t$$ (4)

where (x,y) are the pixel coordinates, λ the laser wavelength, n(x,y) is the cellular, n_l of the surrounding medium refractive index and t is the cell thickness. Notice that to evaluate features of a cell, such as for example its biovolume or its n_n, a decoupling method, able to discard between n-value information from the thickness in Eq. (4) is needed. Different methods have been proposed to simultaneously measure n-values and the sample thickness by adopting a sequential perfusion of two isotonic solutions with different n-values [40], or employing optical manipulations stages with optical tweezers [18].

Table 1. Biophysical monocyte properties from collaborative OS and DH imaging technique for ΔP of 2000 mbar and 0.2 g dL⁻¹ PEO-PBS as well as literature values.

Technique:	dc (µm)	nOS	n/c-ratio	S (µm2)	E	V (µm3)	DM (pg)
OS	9.57 ± 1.02	1.383 ± 0.006	0.784 ± 0.03	—	—	—	—
DH	—	—	—	71.96 ± 12.54	0.917 ± 0.036	482.42 ± 57.94	87.99 ± 19.09
Doowney et al. [43]	8.13
Inglis et al. [44]	10.40
Loiko et al. [45]	9.87	1.370

However, in our experiment we cannot optically manipulate cells or change the culture medium, thus we cannot directly measure such parameters. In this case, we use the results obtained from OS measurements, i.e. the average measure of the cell n-value n_OS, as input for the calculation of cell volume (V). In our case, a n_c of 1.360 and n_n of 1.389 were obtained. Definitively, V can be measured from QPI by using the following equation:

$$V=\frac{\text{λ}}{2\pi \left(n_{OS}-n_l\right)}\widehat{\text{φ}}S$$ (5)

where surface area (S) and the average phase value $\hat{\phi }$ are defined as:

$$S=K{\rho }^2$$ (6)

$$\widehat{\text{φ}}=\frac{1}{K}{\displaystyle {\sum }_{j=1}^K\text{Δ}{\text{φ}}_j}$$ (7)

in which K is the total number of pixels within a cell, ρ denotes the pixel size in the reconstruction image plane and Δφ_j is the phase value of each pixel within the monocyte. Notice that S, as well as V, cannot be measured directly from the OS data. In addition, QPI can be used to measure other two biophysical characteristics of monocytes, i.e. the ellipticity (E) and the dry mass (DM), defined as:

$$E=a_{\text{min}}/a_{\text{max}}$$ (8)

$$DM=\frac{10\text{λ}}{2\text{λα}}\widehat{\text{φ}}\mathrm{S}$$ (9)

where a_min and a_max are the minor and the major axis length of the monocyte, respectively, and α = 0.2mL g⁻¹ is known as the specific refractive index increment [40].

By using OS outcomes and Eqs. (5)-(9) from DH data, we were able to fully characterize monocytes in flow in terms of their biophysical properties. Table 1 reports measured biophysical monocyte parameters for DH and OS as well as literature values. Our outcomes of cell dimension are in good agreement with literature values, even if a profound comparison of all the other biophysical cell properties is challenging due to the lack of data. Compared to lymphocytes [28] a significantly bigger d_c value and smaller n_n as well as n/c-ratio has been detected, allowing an accurate label-free cell identification in flow.

4. Conclusion

We investigated individual monocytes in a microfluidic-based measurement system with the aim to fully characterize their morphometric and optical properties, and to track their position in flow in a label-free modality. For this purpose, we employed two coherent imaging techniques, i.e. OS and DH. All results were obtained at two fixed measurement positions, the first one selected close to the exit of the capillary (x₀) to ensure the stability of 3D cell alignment without any effect of cell deformation, a necessary condition for the accuracy of OS measurements; the second one placed far from capillary (x₁) to study the cell position variations as a function of flow pressure, through holographic tracking [36]. Both imaging modalities were able to provide a label-free investigation of monocytes, thus allowing a comparison among them. The possibility of investigating monocyte shape with high resolution offers interesting opportunities for their characterization and quantification. Consequently, a clear identification of the monocyte state can be assured, as a hint for better comprehension of possible pathologic conditions. The proposed microfluidic approach confirms the precise 3D alignment for different applied cell velocities, as observed in our previous study [28,31] In addition, by comparing the current results with those reported in ref [28,31], a label-free way to differentiate and fully characterize lymphocytes, monocytes and erythrocytes in vertical downstream flow may be realistic and it will be investigated in future works.

Disclosures

The authors declare that there are no conflicts of interest related to this article.