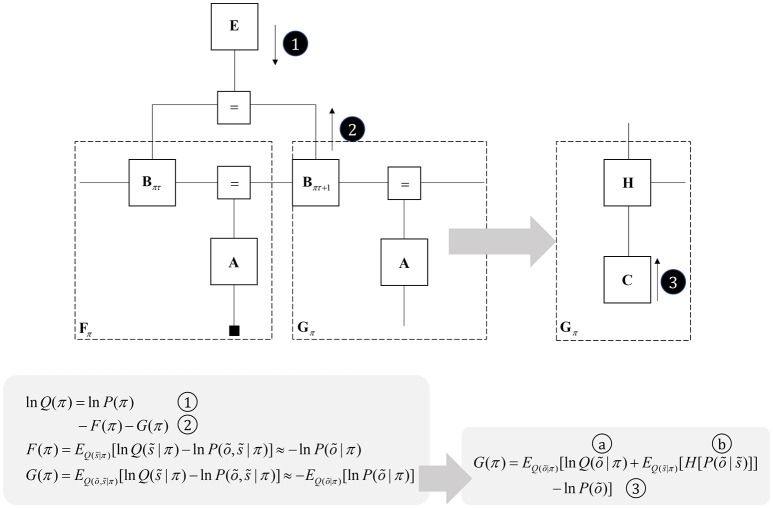
Figure 5.

Planning as inference. This figure illustrates the use of partition functions to evaluate regions of the graph (see also Figure 2). Crucially, while we can approximate a partition functions based upon past data using a free energy functional, we do not yet have data from the future. This means we instead need an expected free energy, to approximate the partition function under posterior predictive beliefs. The panel below the graph illustrates how we can re-express the expected free energy such that we can represent this portion of the graph in terms of two new factors: a marginal belief about future outcomes and a likelihood that becomes an expected entropy after taking the expectation. As G depends upon beliefs about outcomes, but not upon the outcomes themselves, we can compute this prior to observing data. In some accounts of active inference, this is made explicit by treating C as a prior that connects to a factor G (that acts as if it were a likelihood generating policies from outcomes). The circled numbers and letters here are consistent with those in Figure 6. For technical accounts of these equations, please see Friston et al. (2017d), Parr and Friston (2018c).