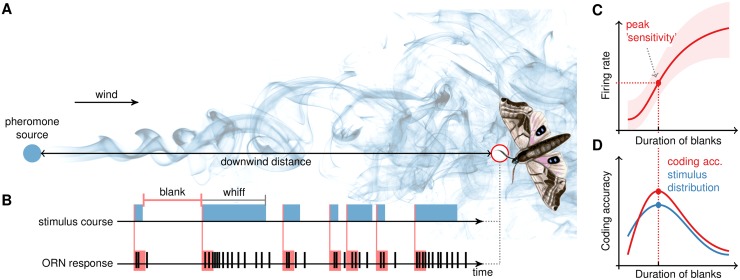
Fig 1. Graphical abstract.

(A) Atmospheric turbulence governs the complicated non-homogeneous dispersion of a pheromone, which is detected by specialized olfactory receptor neurons (ORNs) located on the moth antennae (red circle). (B) A typical time course of the pheromone stimulation at a given distance from the source is intermittent. The signal consists of blanks, intervals of zero local concentration due to the passage of clean-air pockets, and of whiffs, intervals of pheromone presence. The statistics of blanks and whiffs describes the spatio-temporal structure of the turbulent plume. (C) A simple encoding model of a whiff encounter is given by the dependence of the firing rate (measured within a period after the whiff onset) on the preceding blank duration, the duration-rate relationship. The coding sensitivity of the whiff encounter is determined from the slope of the mean response and the response variability. In order to detect the pheromone optimally, the efficient coding hypothesis predicts the ORN to adjust its encoding sensitivity to the local stimulus conditions by adjusting the duration-rate relationship. (D) We observe that encoding properties of ORNs are adjusted to match the local distribution of blank durations. Particularly, i) the maximal sensitivity corresponds to the most frequent blank duration (stimulus timescale), cf. Figs 4 and 5; ii) the average decoding accuracy is largest for the matching stimulus-timescale distribution (Fig 6); and iii) the profile of the coding accuracy matches the stimulus-timescale distribution optimally from an information-theoretic point of view (Figs 7 and 8). (The figure is meant only as an illustration of the studied problem and does not represent the measured data.)