Irving-Williams Order in the Framework of Connectivity Index ³χ^v Enables Simultaneous Prediction of Stability Constants of Bivalent Transition Metal Complexes

Abstract

Logarithms of stability constants, log K₁ and log β₂, of the first transition series metal mono- and bis-complexes with any of four aliphatic amino acids (glycine, alanine, valine and leucine) decrease monotonously with third order valence connectivity index, ³χ^v, from Cu²⁺ to Mn²⁺. While stability of the complexes with the same metal is linearly dependent on ³χ^v, stability constants of Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺complexes with the same ligand show a quadratic dependence on ³χ^v. As Cu²⁺ complexes deviate significantly from quadratic functions, models for the simultaneous estimation of the stability constants, yielding r = 0.999 (S.E. = 0.05) and r = 0.998 (S.E. = 0.11), for log K₁ and log β₂, respectively, were developed only for Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ complexes with amino acids.

1. Introduction

The Irving-Williams order of stability of bivalent transition metal complexes (Mn²⁺<Fe²⁺<Co²⁺ <Ni²⁺<<Cu²⁺>Zn²⁺) [1,2] is an empirical rule well known to every chemist, but it was rarely used for the quantitative prediction of stability constants. Cannon developed an interpolation formula [3] to predict stability constants of chromium(II) complexes from the constants of copper(II), manganese(II), and zinc(II), but it was later found to be in no way better than similar formulas based on one variable, namely stability constants of copper(II), or merely protonation constant of the ligand [4].

In our systematic attempt to develop regression models based on the third order valence connectivity index (³χ^v) for the prediction of stability constants of coordination compounds [5,6], we were concerned mostly with the copper(II) and nickel(II) chelates. We developed models not only for the complexes of the same metal, but also the simultaneous prediction of stability constants of copper(II) and nickel(II). This was done by introducing an indicator variable, i.e. assuming that the regression lines for the two metals have the same slope [7,8].

Connectivity, as well as other topological indices [9,10], have found wide range of application in all fields of chemisty [11,12,13,14], but they were not used for the prediction of stability constants of coordination compounds before the appearance of our pioneering work in 1999 [15]. Even now, many chemists are reluctant to use such a simple method, as models based on topological indices really are, to solve such a complex problem as prediction of stability of coordination compounds.

However, regression models based on valence connectivity index of the third order are capable of predicting stability constants with an error usually less than 0.3 log K units, and were even successfully used for the evaluation of experimental data obtained by two different electrochemical methods, potentiometry and voltammetry [16]. The regression models were successfully checked on complexes of α-amino acids and their N-alkylated derivatives [16,17], amines [17,18,19] and smaller peptides from dipeptides to pentapeptides [7,20]. Also, we recently applied our model to cadmium(II) complexes with amino acids [21].

The aim of this paper is to make our regression models based on ³χ^v index more general, i.e. to develop models that would discriminate not only ligands, but metals as well. As complexes of the metals from Irving-Williams order seems ideal for this purpose, we choose stability constants of their mono-

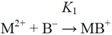(1)

and bis-complexes

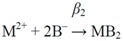(2)

with aliphatic α-amino acids (M stays for metal and B for ligand).

2. Methods

2.1. Calculation of topological indices

We calculated topological indices using a program system E-DRAGON, developed by Todeschini and coworkers [22,23], which is capable of yielding 119 topological indices in a single run, along with many other molecular descriptors [24,25]. Connectivity matrices were constructed with the aid of the Online SMILES Translator and Structure File Generator [26]. All models were developed by using ³χ^v index (the valence molecular connectivity index of the 3^rd order), which was defined as [27,28,29]:

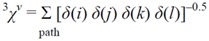(3)

where δ(i), δ(j), δ(k), and δ(l) are weights (valence values) of vertices (atoms) i, j, k, and l making up the path of length 3 (three consecutive chemical bonds) in a vertex-weighted molecular graph.Valence value, δ(i), of a vertex i is defined by:

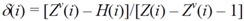(4)

where Z^v(i) is the number of valence electrons belonging to the atom corresponding to vertex i, Z(i) is its atomic number, and H(i) is the number of hydrogen atoms attached to it. For instance, δ values for primary, secondary, tertiary and quaternary carbon atoms are 1, 2, 3, and 4, respectively; for oxygen in the OH group it equals 5, and for NH₂ group δ(N) = 3. It has to be pointed out that ³χ^v is only a member of the family of valence connectivity indices ⁿχ^v, which differ between each other by the path length, i.e. the number of δ´ sin the summation term, Equation (3).

The ³χ^v indices for all mono- and bis-complexes were calculated from the graph representations of the aqua complexes with two water molecules (Figure 1), assuming that metal in mono-complexes is tetracoordinated, and in bis-complexes hexacoordinated [17,30].

Figure 1.

The graph representations for metal(II) mono- (MB) and bis-complex (MB₂) with glycine. Heteroatoms are marked with (M), (N), and (O).

2.2. Regression calculations

Regression calculations, including the leave-one-out procedure of cross validation, cv, were done using the CROMRsel program [31]. The standard error of cross validation estimate is defined as:

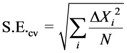(5)

where ΔX and N denotes cv residuals and the number of reference points, respectively.

2.3. Stability constants selection

Because of huge variations between experimental stability constants it was important that selected constants were measured under the same conditions (ionic strength, temperature), and preferably in the same laboratory. It was a bit surprising to find out that the most consistent constants were also the oldest, determined in 1950s. They were measured at t = 25 °C, and I = 0.01 or I → 0 mol L⁻¹. If more than one experimental value was referred for a complex, we used mean value in further calculations. Moreover, lack of constants measured at these conditions forced us to include three constants, for Fe(Glycine), Fe(Glycine)₂ and Fe(Valine), measured at t = 20 °C, I = 0.01 mol L⁻¹. Unfortunately, appropriate log K₁ andlog β₂ values for Ni²⁺ complexes with valine were not found in the literature.

3. Results and Discussion

In this paper we tried to reproduce stability constants of chelates with bivalent metals constituting Irving-Williams order, whose stability grows monotonously (from Mn²⁺ to Cu²⁺), by means of valence connectivity index of the 3^rd order, ³χ^v. Therefore, experimental values of stability constants of the metal complexes with four aliphatic α-amino acids (glycine, alanine, valine and leucine) were taken from the literature, Table 1.

Table 1.

Experimental stability constants for metal(II) chelates with α-amino acids.

Metal/Ligand	log K1	log β2	References
Cu/Glycine	8.57	15.63	[32,33,34,35]
Ni/Glycine	6.15	11.15	[32,33]
Co/Glycine	5.09	9.10	[32,33]
Fe/Glycine	4.30	7.80	[36]
Mn/Glycine	3.55	6.63	[32,33]
Cu/Alanine	8.41	15.21	[32,33,37,38]
Ni/Alanine	5.96	10.66	[33]
Co/Alanine	4.83	8.55	[32,33,39]
Fe/Alanine		7.30	[39]
Mn/Alanine	3.13	6.05	[32,33]
Cu/Valine	7.93	14.45	[32]
Co/Valine	4.57	8.24	[32]
Fe/Valine		6.80	[39]
Mn/Valine	2.84	5.56	[32]
Cu/Leucine	7.89	14.34	[32]
Ni/Leucine	5.62	10.18	[40]
Co/Leucine	4.52	8.16	[32,40]
Mn/Leucine	2.78	5.45	[32]

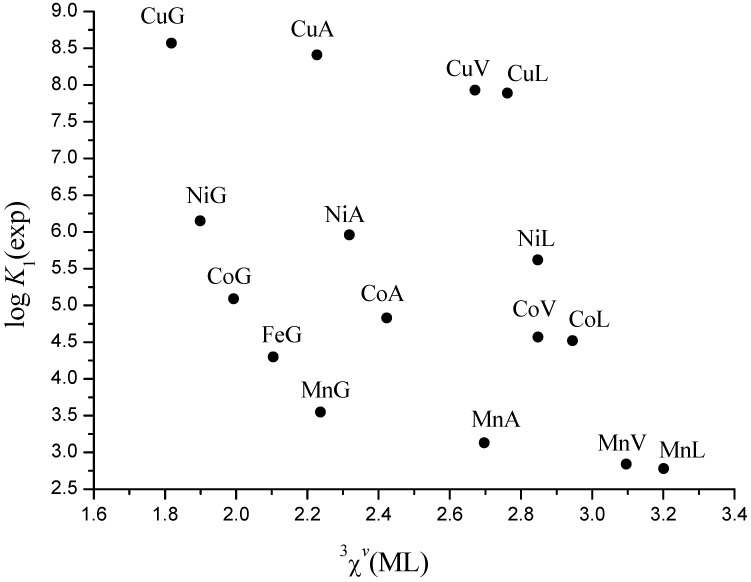
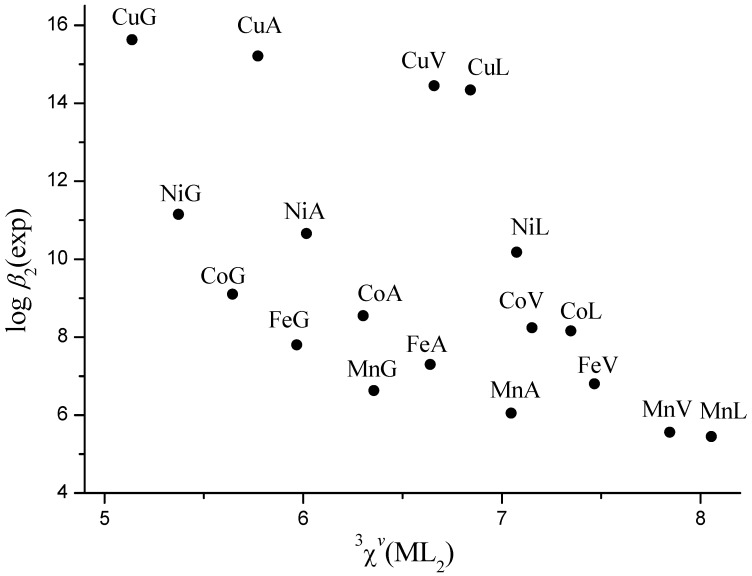
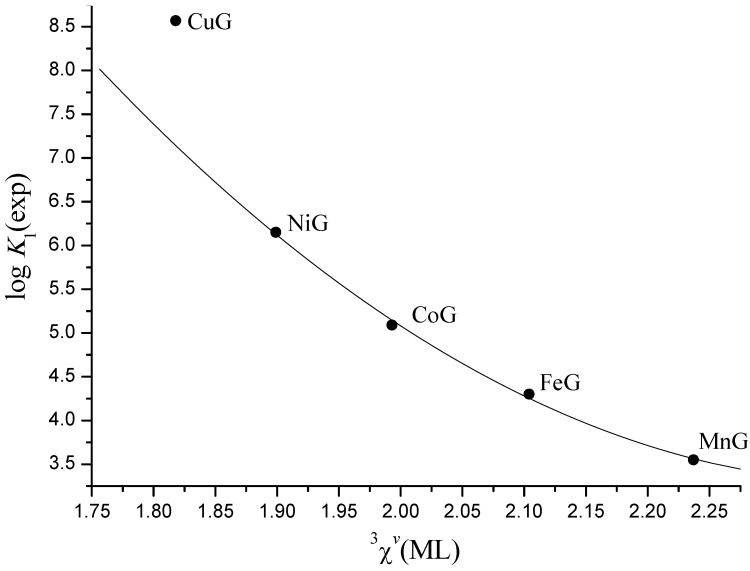
It is evident (Figure 2 and Figure 3), that stability constants of the complexes with the same metal decrease linearly with ³χ^v from glycine to leucine, as we have previously shown [17,30]. Figure 2 and Figure 3 also show that stability of mono- and bis-complexes decreases monotonously from Cu²⁺ to Mn²⁺ for complexes with the same ligand. However, the decrease is much more pronounced between Cu²⁺ and Ni²⁺ because Cu(II) is the strongest Lewis acid in Irwing-Williams order, and its complexes are therefore unusually stable [2]. Consequently, stability constants of Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ complexes show quadratic dependence on ³χ^v, but Cu(II) complexes considerably deviate from it (Figure 4).

Figure 2.

Experimental values of log K₁ vs. connectivity ³χ^v index for Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺, and Cu²⁺ complexes with glycine (G), alanine (A), valine (V) and leucine (L).

Figure 3.

Experimental values of log β₂ vs. connectivity ³χ^v index for Mn²⁺, Fe²⁺, Co²⁺, Ni²⁺, and Cu²⁺ complexes with glycine (G), alanine (A), valine (V) and leucine (L).

Figure 4.

Quadratic dependence of log K₁ of Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ complexes with glycine (G) on connectivity index ³χ^v.

Bearing this in mind we developed models for the simultaneous estimation of stability constants of Mn²⁺, Fe²⁺, Co²⁺ and Ni²⁺ complexes:

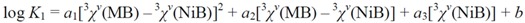(6)

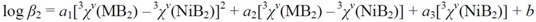(7)

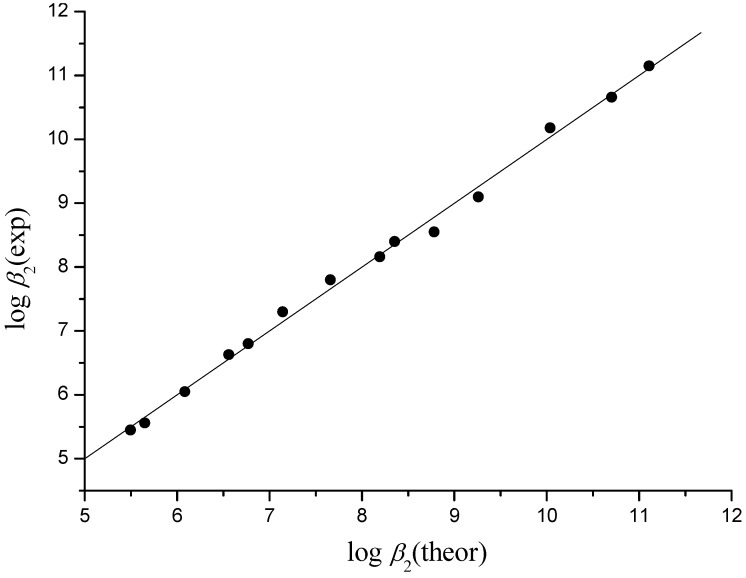
where ³χ^v(NiB) and ³χ^v(NiB₂), stand for normalization along x axis in the first two terms, and for normalization along y axis in the third terms. Models gave standard error of cross validation S.E._cv = 0.08 and 0.15, and maximal cv error of 0.13 and 0.29 for log K₁ and log β₂, respectively (Table 1, Table 2 and Table 3, Figure 5 and Figure 6).

Table 2.

Regression models for the estimation of the stability constants of mono- and bis-complexes.

Eq.	N	Dependentvariable	Regression coefficients			Intercept (S.E.)	r	S.E.	S.E.cv
			a1(S.E.)	a2(S.E.)	a3(S.E.)
(6)	12	log K1	12.2(14)	−12.10(55)	−0.676(46)	7.49(12)	0.999	0.05	0.08
(7)	14	log β 2	3.10(33)	−7.66(36)	−0.646(52)	14.58(33)	0.998	0.11	0.15

Table 3.

Theoretical (cross validated) stability constants for metal(II) chelates with α-amino acids, and their ³χ^v indices.

Metal/Ligand	log K1 (cv)	log β2 (cv)	3χv(MB)	3χv(MB2)
Ni/Glycine	6.21	11.11	1.90	5.37
Co/Glycine	5.18	9.25	1.99	5.65
Fe/Glycine	4.24	7.65	2.10	5.97
Mn/Glycine	3.51	6.58	2.24	6.36
Ni/Alanine	5.93	10.69	2.32	6.02
Co/Alanine	4.79	8.76	2.42	6.30
Fe/Alanine		7.13	2.55	6.64
Mn/Alanine	3.09	6.10	2.70	7.05
Ni/Valine			2.75	6.89
Co/Valine	4.59	8.32	2.85	7.15
Fe/Valine		6.74	2.96	7.47
Mn/Valine	2.91	5.64	3.10	7.85
Ni/Leucine	5.57	10.01	2.85	7.08
Co/Leucine	4.50	8.16	2.95	7.35
Mn/Leucine	2.81	5.48	3.20	8.06

Figure 5.

Experimental vs. theoretical (fit) log K₁ for Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ complexes with glycine, alanine, valine and leucine; r = 0.999, S.E._cv = 0.08.

Figure 6.

Experimental vs. theoretical (fit) log β₂ for Mn²⁺, Fe²⁺, Co²⁺, and Ni²⁺ complexes with glycine, alanine, valine and leucine; r = 0.998, S.E._cv = 0.15.

4. Conclusions

Our regression models, Equations (6) and (7), clearly show that by using the connectivity index ³χ^v it is possible to predict stability constants with an error 0.03–0.13 and 0.00–0.29 for log K₁ and log β₂, respectively, i.e. virtually within the limits of experimental error. Besides, maximal range of experimental values, 0.28 for log K₁ of Co(Glycine) and 0.38 for log β₂ of Co(Alanine)₂, speaks strongly in favor of our model. All this leads to the conclusion that models for the prediction of stability constants based on connectivity index ³χ^v could provide a chemist the simple and efficient tool for planning his experiments and discussing his results.