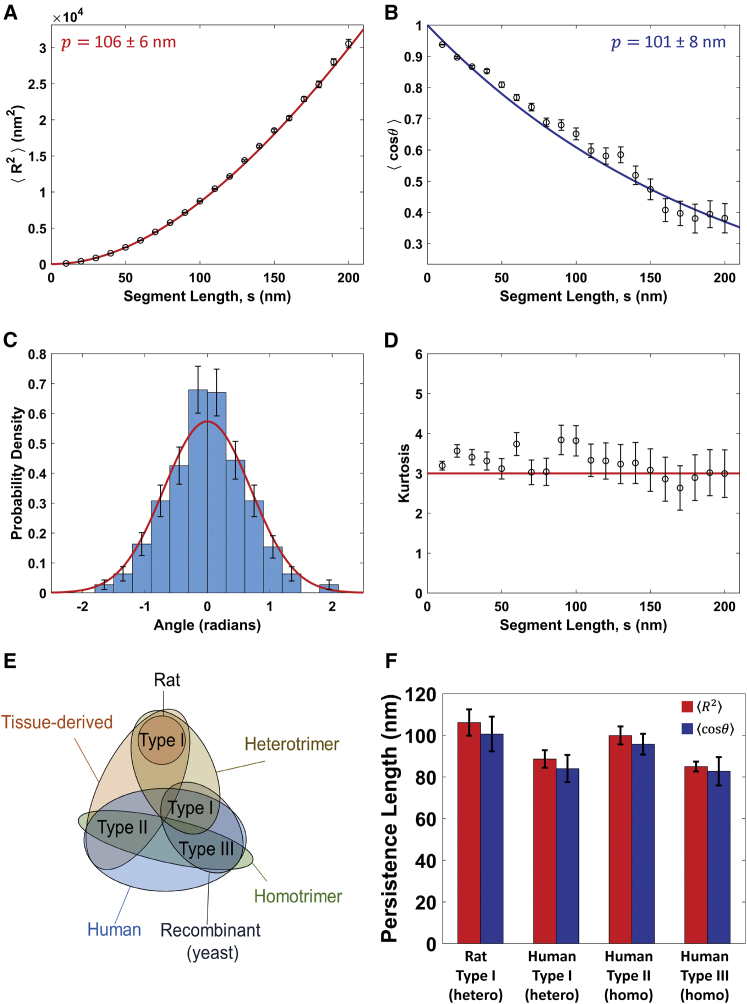
Figure 2.

Determination of collagen’s persistence length using the standard worm-like chain (WLC) model. (A–D) Analysis for rat type I collagen deposited from a solution of 100 mM KCl + 1 mM HCl. (A) Mean-square end-to-end distance as a function of segment length, $\langle R^2\left(s\right)\rangle$. Points represent mean values determined at 10 nm segment-length intervals, with error bars representing standard errors of the mean. The red line is a fit with Eq. 1, yielding a persistence length of p = 106 ± 6 nm (error represents 95% confidence interval of the fit). (B) Tangent vector correlation as a function of segment length, $\langle \cos \theta \left(s\right)\rangle$. Points and errors are similarly represented as in (A). The blue line is a fit with Eq. 2, yielding p = 101 ± 8 nm. Fits to the WLC model in (A) and (B) capture the trends in the data and yield comparable persistence lengths. (C) An angular histogram for s = 50 nm segment lengths (blue bars). Error bars represent $\sqrt{N}$ counting error. This distribution agrees well with that expected for a WLC of persistence length p = 103 nm (the average of the results from (A) to (B)), which is a normal distribution with a mean of zero and a variance of s/p (red line). (D) Kurtosis of the angular distributions extracted from the traced collagens at different segment lengths is shown. Error bars represent the standard error in the kurtosis (Eq. S19). The kurtosis of the angular distributions is close to three (red line) for all segment lengths, indicating that the collagens behave as equilibrated Gaussian chains on the mica surface. (E) A Venn diagram illustrating the similarities and differences between the different collagen samples tested, including trimeric identity and source. (F) Persistence length for each collagen sample deposited from a solution of 100 mM KCl + 1 mM HCl, obtained using $\langle R^2\left(s\right)\rangle$ and $\langle \cos \theta \left(s\right)\rangle$ analyses. The similarity among these samples suggests that collagen type and source have little impact on the mechanical properties of collagen at the molecular level. To view this figure in color, go online.