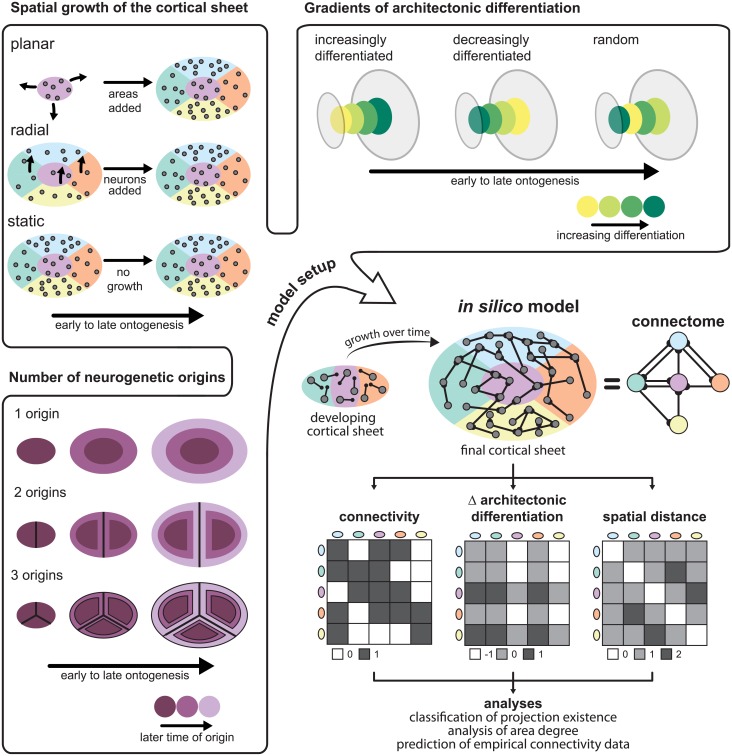
Fig 1. Neurodevelopmental assumptions and overview of the in silico model.

The figure illustrates the assumptions regarding neurogenesis that were varied in the in silico model. The spatial growth of the cortical sheet of a single hemisphere was modelled in three possible ways: First, planar growth, in which the neurons comprising a cortical area develop at the same time and the cortical sheet expands as more areas materialize. Second, radial growth, in which neurons across the entire extent of the final cortical sheet develop at the same time, and the final complement of neurons is reached by gradual growth of neurons at a constant rate. Third, no growth, that is, a static cortical sheet on which the final complement of neurons is already present from the onset. Regarding the gradients of architectonic differentiation, we considered three possible relationships between the time at which an area was formed (time of neurogenesis) and its architectonic differentiation, approximated by neuron density. First, areas could be more differentiated the later in ontogenesis they were formed (increasingly differentiated). This scenario corresponds to the realistically oriented density gradient we incorporated in the in silico model. Second, areas could be less differentiated the later their time of origin was (decreasingly differentiated). This scenario corresponds to the inversely oriented density gradient in the in silico model. Third, there could be no gradient of differentiation aligned with neurogenetic timing, that is, the neuron density of newly formed areas varied randomly throughout ontogenesis. As a third factor that determined the spatiotemporal growth trajectory of the cortical sheet, we considered the number of neurogenetic origins. There could either be a single origin, such that more recently formed areas occupied the fringes of the cortical sheet, or there could be two or three origins. In this case, recently formed areas would be interleaved with areas that were formed earlier, as the neurogenetic origins were moved apart by addition of areas around them. From these assumptions on neurogenetic processes shaping the cortical sheet, we set up different variants of an in silico model in which axons grew randomly across the developing cortical sheet and stochastically formed connections. We translated the resulting neuron-level connectivity to area-level connectivity and extracted structural measurements from the simulated cortical sheet. As in previous studies of mammalian connectomes, we considered the difference in architectonic differentiation between areas and their spatial distance. Thus, we simulated sets of measures which we could then analyse in the same way as the empirical data, and compared the results to empirical findings. Specifically, we used simulated architectonic differentiation and spatial distance to classify whether a connection existed in the final simulated network; we probed whether there was an association between simulated architectonic differentiation and the number of connections maintained by an area; and we used a classifier trained on the simulated data to predict connection existence in two sets of empirical connectivity data, from the cat and the macaque cortex.