New framework reveals global warming’s impact on risk that multiple regions experience hot and dry conditions simultaneously.
Abstract
We present a framework for quantifying the spatial and temporal co-occurrence of climate stresses in a nonstationary climate. We find that, globally, anthropogenic climate forcing has doubled the joint probability of years that are both warm and dry in the same location (relative to the 1961–1990 baseline). In addition, the joint probability that key crop and pasture regions simultaneously experience severely warm conditions in conjunction with dry years has also increased, including high statistical confidence that human influence has increased the probability of previously unprecedented co-occurring combinations. Further, we find that ambitious emissions mitigation, such as that in the United Nations Paris Agreement, substantially curbs increases in the probability that extremely hot years co-occur with low precipitation simultaneously in multiple regions. Our methodology can be applied to other climate variables, providing critical insight for a number of sectors that are accustomed to deploying resources based on historical probabilities.
INTRODUCTION
It is now clear that global-scale warming has led to changes in regional climate, including temperature, precipitation intensity, sea level, sea ice, snowpack, drought risk, and extreme events (1, 2). Given this regional-scale climate change, a key question for building resilience in the current climate, as well as preparing for future climate change, is the extent to which global warming has caused changes in the spatial and temporal co-occurrence of climate stresses. This co-occurrence is critical for a broad suite of climate-sensitive concerns, including agricultural markets (3), food security (4, 5), poverty vulnerability (6), supply chains (7), weather-related insurance and reinsurance (8), and disaster preparedness and recovery.
Accounting for nonstationarity in multiple dimensions presents a key challenge for quantifying changes in the joint probability of climate stresses across space and time (9). In the past decade, considerable progress has been made in quantifying the risk of hydroclimatic extremes using univariate metrics under nonstationary conditions [e.g., (10)]. In addition, multivariate statistical methods have been used to model the probability of multiattribute climatic and hydrologic phenomena [e.g., (11–14)], including the co-occurrence of climate extremes [e.g., (15, 16)]. Although much has been learned, accounting for temporal nonstationarity in a multidimensional context that captures changes in the dependence structure between multiple variables across different locations has remained a persistent challenge (17–19).
In the current study, we present a multidimensional risk framework for addressing this challenge. We focus on quantifying changes in the joint probability of warm and dry conditions, both in an individual location and simultaneously in multiple locations. The sensitivity of natural and human systems to warm and dry conditions [e.g., (20, 21)] provides compelling motivation for exploring whether anthropogenic forcing has altered the probability that those conditions occur simultaneously in different parts of the world. In addition, our framework could be readily applied to other climatic or nonclimatic variables.
In light of international efforts to curb global warming, it is important to quantify changes in the joint probability of climate stresses at different levels of climate forcing. Quantifying how the probability of co-occurring stresses has changed during the historical period is critical both for managing risks in a nonstationary climate and for understanding the impacts of historical global warming. Similarly, quantifying the likelihood of changes in future emissions scenarios is critical for both evaluating the benefits of achieving mitigation targets such as those in the United Nations (UN) Paris Agreement and managing the resulting risks should those targets ultimately be achieved.
Our framework uses the vine copula to quantify the time-varying joint probability of co-occurring climate stresses across multiple dimensions under nonstationary conditions (see Materials and Methods). We use this framework to quantify changes in the probability that warm and dry years co-occur in an individual location and simultaneously in different locations. We analyze these changes in joint probability in historical observations, the Coupled Model Intercomparison Project, Phase 5 (CMIP5) Historical and Natural climate model simulations, and the CMIP5 future climate projections (see Materials and Methods).
RESULTS
The pattern of observed trends in the probability of warm years (Fig. 1A) largely resembles that of long-term warming (2). Aggregated over all areas for which observational data are available for the full 1931–2015 period, the probability of a warm year (relative to a given area’s 1961–1990 mean) has increased from ~50% during the mid-20th century to >80% in the 21st century (Fig. 1D). The time evolution of warm year probability in the Historical climate model ensemble closely matches that of the observations, increasing from ~40% in the mid-20th century to ~80% in the early 21st century (Fig. 1G). In contrast, the warm year probability remains centered around 20% (relative to a given area’s 1961–1990 mean) throughout the Natural ensemble, with the 2.5th to 97.5th percentile confidence intervals of the Historical and Natural ensembles remaining completely separated after ~1970. There is thus high statistical confidence that the observed increase in warm year probability would not have occurred without anthropogenic forcing.
Fig. 1. Historical changes in warm year probability, dry year probability and joint probability.
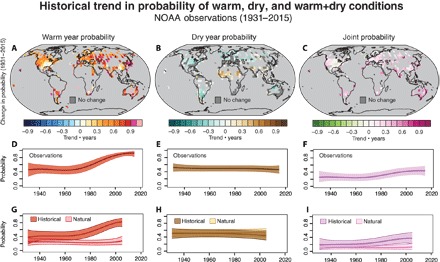
(A to C) Change in warm year probability, dry year probability, and joint probability, calculated as the trend over the period (1931–2015) using Sen’s slope estimator times the length of the period. Maps show results for the 50th percentile of the Bayesian sampling. Dark gray indicates no change in the location parameter through time (see Materials and Methods). (D to F) Global average of the warm year probability, dry year probability, and joint probability aggregated across the grid points in the National Oceanic and Atmospheric Administration (NOAA) observations. The bold line shows the posterior mean, and the color envelope shows the 2.5th to 97.5th percentile range (see Materials and Methods). (G to I) Global average of the warm year probability, dry year probability, and joint probability aggregated across the grid points in the Historical and Natural forcing experiments of the CMIP5 global climate model ensemble. The bold line shows the ensemble-mean posterior mean, and the color envelope shows the ensemble-mean 2.5th to 97.5th percentile range (see Materials and Methods).
In contrast, the probability of dry years has remained ~50% at the global scale throughout the observational period (relative to the 1961–1990 baseline; Fig. 1E), with areas of the tropics and subtropics exhibiting increases and much of the extratropics exhibiting decreases or no change (Fig. 1B). Although both the observations and the Historical climate model ensemble exhibit slight indications of a decrease in dry year probability in the late 20th and early 21st centuries, the 2.5th to 97.5th percentile confidence intervals of the Historical and Natural ensembles overlap substantially throughout the historical period (Fig. 1H).
Despite the spatial heterogeneity of trends in dry year probability (Fig. 1B), the increasing trends in warm year probability (Fig. 1A) lead to broad increases in the probability of years that are both warm and dry (“warm+dry”; Fig. 1C). At the global scale, the aggregated warm+dry probabilities are similar to what would be expected from the product of the two univariate probabilities (Fig. 1, D and E), with global warm+dry probability equaling ~20% in the mid-20th century and ~40% in the early 21st century (relative to the 1961–1990 baseline; Fig. 1F). At the regional scale, the largest increases in warm+dry probabilities are generally associated with the largest increases in warm year probabilities, although the lack of data in the tropics likely limits the number of grid points that exhibit increases in both univariate probabilities. The most prominent exception to the general increase in warm+dry probability is the well-documented “warming hole” over the central and southeastern United States, where the warm, dry, and warm+dry probabilities all exhibit decreasing trends over the 1931–2015 period (Fig. 1C).
The increase in global warm+dry probability would be expected to increase the odds that different regions experience warm+dry years simultaneously. Given the negative impacts of co-occurring warm+dry conditions on agricultural yields (21) and the importance of co-occurring yield shocks for regional and global agricultural markets [e.g., (3–5)], we quantify the joint probability of warm+dry conditions in pairs of global crop and pasture regions (see Materials and Methods). We find that these regions have become substantially more likely to experience warm+dry anomalies in the same year over the historical period (Fig. 2).
Fig. 2. Historical changes in joint probability of years that are both warm and dry occurring simultaneously in different regions of the world.
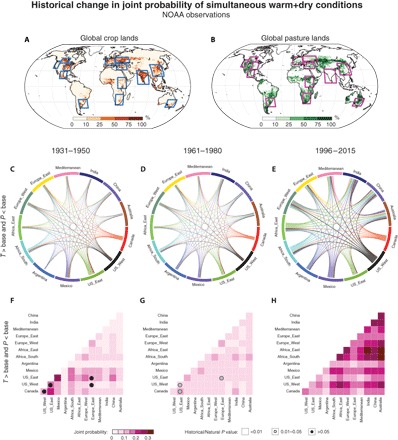
(A and B) Maps showing global cropland and pasture areas in the year 2000 [redrawn from (32)], along with the regions used in our analysis. (C to E) Thickness of lines shows the probability (based on the Bayesian posterior mean) that both regions of a respective region-region pair experience simultaneous warm and dry conditions in the same year during the 1931–1950, 1961–1980, and 1996–2015 periods, based on NOAA observations. Each region pair shares a single joint probability. The color of each region-region joint probability is shown as the color of the first region on the circular plot, starting with Canada and moving clockwise around the circular plot. Thus, all region-region joint probabilities involving Canada are shown in red, and all involving US_West are shown in dark gray except for Canada-US_West, etc. The values of the region-region joint probabilities are shown in (F) to (H). (F to H) Colors show the probability values depicted by lines in (C) to (E). Symbols show the P value of the difference in joint probability between the CMIP5 Historical and Natural simulations for the 1931–1950, 1961–1980, and 1986–2005 periods (see Materials and Methods). The absence of a symbol indicates P value less than 0.01, a gray circle indicates P value between 0.01 and 0.05, and a black circle indicates P value greater than 0.05.
Previous work shows that the occurrence of extreme years—and especially extremely warm years—is particularly important for the volatility of agricultural yields and hence prices [e.g., (5, 22)]. We therefore analyze the joint probability of progressively larger climate anomalies. Like the co-occurrence of years that are warmer and drier than the historical mean (Fig. 2), we find that the joint probability of simultaneous occurrence of these more extreme combinations of temperature and precipitation has also increased during the historical period (Fig. 3). For example, the joint probability of a year in which the temperature exceeds 2 standard deviations (SDs) of the baseline variability and the precipitation is drier than the baseline mean has increased from <5% for all region pairs in the 1931–1950 and 1961–1980 periods to >10% for 31% of the region pairs in the 1996–2015 period (Fig. 3A). Similarly, the joint probability of a year in which the temperature exceeds 2 SDs of the baseline variability and the precipitation is at least 1 SD drier than the baseline mean has increased from <1% for all region pairs in the 1931–1950 and 1961–1980 periods to >1% for 42% of the region pairs in the 1996–2015 period (Fig. 3B). Further, whereas most region pairs exhibit zero probability during the 1931–1950 and 1961–1980 periods that a year exceeds 4 SDs of the baseline temperature variability and is simultaneously drier than the baseline mean, all region pairs exhibit >0% probability during the 1996–2015 period, including >1% probability in 12% of the region pairs (Fig. 3C).
Fig. 3. Historical change in joint probability of simultaneous warm+dry conditions of varying severity.
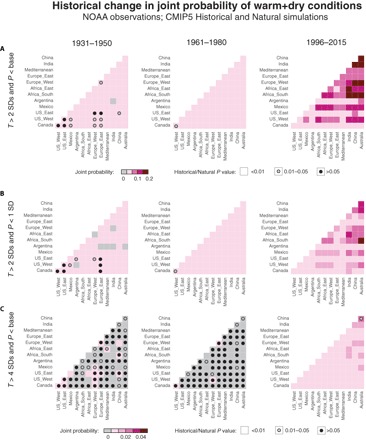
Colors show the probability (based on the Bayesian posterior mean) that both regions of a respective region-region pair experience simultaneous warm and dry conditions in the same year during the 1931–1950, 1961–1980, and 1996–2015 periods, based on NOAA observations. (A) Joint probability for years in which the temperature anomaly is at least 2 SDs warmer than the baseline mean and the precipitation anomaly is drier than the baseline mean. (B) Joint probability for years in which the temperature anomaly is at least 2 SDs warmer than the baseline mean and the precipitation anomaly is at least 1 SD drier than the baseline mean. (C) Joint probability for years in which the temperature anomaly is at least 4 SDs warmer than the baseline mean and the precipitation anomaly is drier than the baseline mean. The P value of the difference in joint probability between the CMIP5 Historical and Natural simulations is indicated as in Fig. 2.
To test the influence of anthropogenic climate forcings on these historical increases in joint probability, we compare the CMIP5 historical forcing simulations with the CMIP5 natural forcing simulations (see Materials and Methods). We find that the difference between the Historical and Natural climate model ensembles is statistically significant for all region pairs during the 1996–2015 period (Fig. 3). The emergence of an anthropogenic signal during the 1996–2015 period is particularly pronounced for the simultaneous occurrence of a 4-SD temperature anomaly combined with a 1-SD precipitation anomaly (Fig. 3C). These results suggest that historical anthropogenic climate forcing has elevated the risk that increasingly severe warm+dry conditions occur simultaneously in multiple regions.
Continued greenhouse gas emissions are likely to further increase the joint probabilities of severely warm+dry conditions (Fig. 4). Relative to the CMIP5 historical simulations, the joint probability of a year in which the temperature simultaneously exceeds 2 SDs of the baseline variability in both regions increases by at least 60 percentage points for all region pairs in the 2020–2050 period of Representative Concentration Pathway 8.5 (RCP8.5), and the joint probability of a year in which the temperature simultaneously exceeds 4 SDs increases by at least 30 percentage points for 90% of the region pairs (Fig. 4A). As a result, the joint probability of a year in which the temperature exceeds 2 SDs and the precipitation is drier than the baseline mean increases by at least 20 percentage points for 21% of the region pairs (Fig. 4C). Likewise, the joint probability of a year in which the temperature exceeds 4 SDs and the precipitation is drier than the baseline mean increases by at least 10 percentage points for 44% of the region pairs (Fig. 4C).
Fig. 4. Projected future change in joint probability of simultaneous warm+dry conditions of varying severity.
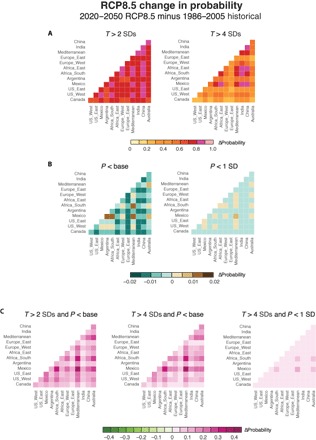
Colors show the probability (based on the Bayesian posterior mean) that both regions of a respective region pair experience severe conditions in the same year during the 2020–2050 period of the RCP8.5 simulations, expressed as the absolute difference from the probability in the CMIP5 historical simulations. (A) Joint probability for years in which the temperature anomaly is at least 2 SDs (left column) or 4 SDs (right column) warmer than the baseline mean. (B) Joint probability for years in which the precipitation anomaly is drier than the baseline mean (left column) or at least 1 SD drier than the baseline mean (right column). (C) Joint probability for years in which the temperature anomaly is at least 2 SDs warmer than the baseline mean and the precipitation anomaly is drier than the baseline mean (left column), the temperature anomaly is at least 4 SDs warmer than the baseline mean and the precipitation anomaly is drier than the baseline mean (center column), or the temperature anomaly is at least 4 SDs warmer than the baseline mean and the precipitation anomaly is at least 1 SD drier than the baseline mean (right column).
The lower forcing in the RCP2.6 scenario substantially curbs the increase in joint probability for the most severe thresholds (Fig. 5). For example, the joint probability of a year in which the temperature exceeds 4 SDs of the baseline variability is >20% larger in RCP8.5 than RCP2.6 for 83% of the region pairs and >50% larger in RCP8.5 for 33% of the region pairs (Fig. 5A). Four-SD annual temperature anomalies represent extreme conditions and are likely to cause acute impacts even if they do not occur in conjunction with low precipitation. However, in addition to the increases in the probability of co-occurring extremely hot years, the joint probability of a year in which the temperature exceeds 4 SDs and the precipitation is drier than the baseline mean is >20% larger in RCP8.5 for 72% of the region pairs. Likewise, the joint probability of a year in which the temperature exceeds 4 SDs and the precipitation is at least 1 SD drier than the baseline mean is >20% larger in RCP8.5 for 62% of the region pairs.
Fig. 5. Sensitivity of projected future change in joint probability of simultaneous warm+dry conditions to the level of climate forcing.
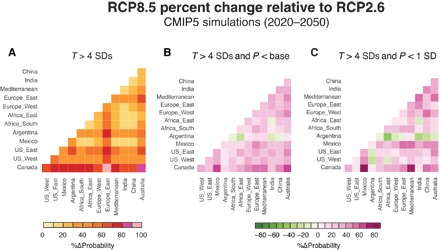
Colors show the probability (based on the Bayesian posterior mean) that both regions of a respective region pair experience severe conditions in the same year during the 2020–2050 period of the RCP8.5 simulations, expressed as the percent difference from the probability in the 2020–2050 period of the RCP2.6 simulations. (A) Joint probability for years in which the temperature anomaly is at least 4 SDs warmer than the baseline mean. (B) Joint probability for years in which the temperature anomaly is at least 4 SDs warmer than the baseline mean and the precipitation anomaly is drier than the baseline mean. (C) Joint probability for years in which the temperature anomaly is at least 4 SDs warmer than the baseline mean and the precipitation anomaly is at least 1 SD drier than the baseline mean.
DISCUSSION AND CONCLUSIONS
Our methodology for calculating the joint probability of co-occurring climate stresses has a number of benefits. Our methodology accounts for nonstationarity within a multivariate risk framework, which is critical given the strong influence of historical global warming on multiple climate variables. Although there has been progress in developing multivariate risk frameworks (15, 18, 23) and in explicitly accounting for nonstationarity in univariate risk frameworks [e.g., (10, 24)], accounting for nonstationarity in a multivariate risk framework has been less common (13, 25).
Our use of the vine copula (see Materials and Methods) provides an advance by enabling quantification of joint probability across four climate variables while accounting for nonstationarity. Our methodology could readily be applied to other climate variables, such as the multiple hazards that can occur simultaneously during landfalling tropical cyclones (i.e., wind speed, storm surge, and precipitation) or the multiple physical ingredients that converge to cause severe precipitation events (e.g., upper-level circulation, lower-level circulation, and atmospheric water vapor). It can also be applied to other geographic co-occurrences of multiple climate stresses (i.e., “compound extremes,” such as the high temperatures, high winds, and low humidity that increase wildfire risk). Caution should be taken, however, in the implementation of normalized metrics, which can introduce artifacts in the quantification of probabilities of extremes [e.g., (26, 27)].
Application of our multidimensional joint probability framework to warm+dry years provides a number of insights. Beyond simply confirming the intuition that long-term warming increases the co-occurrence of warm+dry conditions, our analysis provides explicit quantification of joint probability through time. In particular, our framework reveals that the probability of warm+dry conditions has doubled at the global scale over the historical period and that this doubling has occurred in response to anthropogenic climate forcing. Likewise, our framework reveals that anthropogenic forcing has substantially increased the joint probability that warm+dry conditions occur simultaneously in crop and pasture regions, with key region pairs such as China and India now exhibiting >15% probability of simultaneously experiencing both a 2-SD temperature anomaly and a negative precipitation anomaly in the same year. Last, we find that the probability of extremely warm and dry conditions occurring simultaneously in key crop and pasture regions is substantially greater over the next three decades in RCP8.5 than RCP2.6. The relative reduction in joint probability in the RCP2.6 pathway highlights the benefits of ambitious mitigation in the near-term decades.
The increasing probability that different areas of the globe simultaneously experience multiple climate stresses has important implications for a number of sectors. Given the historical sensitivity of agriculture to episodes of hot, dry conditions, the increase in joint probability of warm+dry years has direct implications for the ability of international trade to buffer the impacts of yield shocks within a region (3–5). Of particular concern is the yield volatility (3, 5, 6, 22), which can increase the risk of commodity price volatility (3, 22), poverty vulnerability (6), and supply chain disruption (7). By increasing the occurrence of low-yield years, increases in the frequency of hot years can increase yield volatility (5, 22), independent of changes in temperature variability. Thus, although we do not explicitly quantify changes in year-to-year temperature variations and although changes in subannual extremes (such as heat waves) are likely to be even more extreme than the annual-scale climate anomalies studied here (22), annual-scale anomalies that exceed 4 SDs of the baseline temperature variability are sufficiently extreme to cause substantial negative yield shocks and associated increases in yield volatility (5, 22).
In addition to agriculture-dependent sectors, the increasing probability of spatially co-occurring climate stresses also has broad implications for sectors and services that are accustomed to deploying resources based on historical probabilities, such as disaster-related preparedness, recovery, and insurance. The fact that historical global warming has already increased the probability of spatially and temporally co-occurring climate stresses highlights the risks of nonstationarity in the current climate, as well as the differential risks associated with different levels of future global warming.
MATERIALS AND METHODS
Overview of framework for multidimensional risk quantification
We developed a new framework for quantifying time-dependent, multidimensional risk in a nonstationary climate and applied this framework to quantify the influence of global warming on the joint probability of warm and dry conditions over the past several decades and in future climate forcing trajectories. Our framework (which is summarized below and described in detail in the Supplementary Materials) is based on the canonical vine (C-vine) copula, which we applied to varying severities of annual-scale temperature and precipitation anomalies to calculate the time-varying joint probability that warm and dry conditions occur simultaneously in pairs of regions. The result is a generalized, fully dynamic multidimensional risk framework that models the time-varying temporal and spatial dependence structure between multiple extremes.
While the application of bivariate copulas is now common, applications of four-dimensional copulas are rare (28). To the best of our knowledge, this is the first introduction of a dynamic four-dimensional vine copula (with a dynamic graphical structure) that evolves through time and quantifies the time-varying dependence structure for multiple climate variables in multiple locations. This methodology allows us to account for nonstationarity in the dependence structure between correlated heavy-tailed multiple extremes, including for thresholds that fall in the extreme tail of the historical distribution. In addition, the application of the Bayesian Markov Chain Monte Carlo (MCMC) allowed us to quantify the uncertainty in estimating time-varying statistical moments and subsequently the joint probability of compound extremes through time. Although in this initial study we analyzed the joint probability of varying severities of warm and dry conditions in multiple locations, our framework is generalizable to other climate variables and to other nonclimatic multidimensional risks.
Data sources
We analyzed observational temperature and precipitation data from the NOAA Global Historical Climate Network–Monthly gridded products, which are available on a 5° by 5° geographical grid (29). We restricted our observational analysis to grid points for which observational data were available for the full 1931–2015 period, with the joint probability analysis restricted to those grid points for which both observational temperature and precipitation data were available. The NOAA temperature and precipitation data were available as monthly anomalies, which we aggregated to annual values. Because the temperature and precipitation data used different baseline periods for calculating the anomalies (1981–2010 for temperature and 1961–1990 for precipitation), we used a simple arithmetic adjustment to express each of the temperature values as an anomaly from the 1961–1990 period (i.e., by adding the difference between the 1981–2010 calendar-month mean and the 1961–1990 calendar-month mean to each monthly temperature value).
We also analyzed climate model data from the CMIP5 (30). To match the NOAA observational data, we calculated monthly temperature and precipitation anomalies using the 1961–1990 baseline. Following many previous studies, we accessed all available CMIP5 realizations and interpolated all climate model realizations to a common 1° by 1° geographical grid. For the regional analyses (see below), we used all the 1° by 1° grid points in each region.
We used four of the CMIP5 forcing experiments (see tables S1 to S3 for a list of realizations). To analyze historical changes in the probability of warm and dry years, we used the Historical and Natural forcing experiments, which were available through the year 2005. The historical forcing experiment includes both natural and anthropogenic climate forcings during the historical period, while the natural forcing experiment includes only the natural climate forcings. We tested the statistical significance of the differences between the Historical and Natural sample populations using the Kolmogorov-Smirnov test (see the Supplementary Materials). For this comparison, we evaluated two categories of statistical significance: P value less than 0.01 and P value between 0.01 and 0.05.
We also compared the probability of warm and dry years in the 2020–2050 period of the RCP2.6 and RCP8.5 future climate forcing scenarios. Of the RCP scenarios archived in CMIP5, RCP8.5 most closely tracks the recent emissions trajectory, while RCP2.6 most closely represents the ambitious mitigation detailed in the UN Paris Agreement (31) (see the Supplementary Materials for additional details).
Analysis of joint probability of warm and dry years
We quantified changes in the joint probability of warm and dry years co-occurring in an individual location (warm+dry years) and co-occuring simultaneously in different locations. We performed this quantification for multiple thresholds of warm and dry severity, including temperature that exceeds the baseline mean by at least 2 SDs of the baseline variability, temperature that exceeds the baseline mean by at least 4 SDs of the baseline variability, and precipitation that is at least 1 SD drier than the baseline mean. We quantified changes in the joint probability of different temperature and precipitation thresholds for the historical observational data, the CMIP5 Historical and Natural climate model simulations, and the CMIP5 future climate projections (see the Supplementary Materials for a complete description).
We first tested whether there have been changes in the probability of warm years and the probability of dry years separately for each area of the globe. For each grid point, we first evaluated whether there has been a trend in the mean of the climate variable (as represented by the location parameter of the distribution). For grid points that do demonstrate a trend in the location parameter, we fitted a polynomial regression model to the time series to model the changes in the location parameter through time. We then applied a Bayesian inference framework to fit a posterior distribution around the value of the location parameter at each year in the time series. We used a time-varying normal distribution for all grid points at which the Kolmogorov-Smirnov test did not reject normality of the residuals and a time-varying Student’s t distribution for all other grid points. The Bayesian posterior mean of the location parameter in the fitted distribution at each year then provides the probability that the temperature anomaly is above the temperature threshold or that the precipitation anomaly is below the precipitation threshold, respectively, at each grid point.
Our approach allows us to model changes in the mean levels of temperature and precipitation over time, and also changes in the dependence between the two. In addition, although we assumed variance with no time trend, the fluctuation of the variance through time was modeled by Bayesian MCMC sampling to ensure that convergence occurs for both the mean and variance (see the Supplementary Materials). It would be possible to extend our approach to model changes in higher moments of the statistical distribution (by, for example, assuming that the relevant scale factor log σ2 depends on the time point), but in practice, none of the grid points in the observational temperature or precipitation dataset exhibit statistically significant trends in the residual time series (fig. S3), supporting our assumption of no time trend in the variance.
To quantify changes in the joint probability of warm+dry years, we used the best-fitted trend models for the location parameter of the marginal distributions of temperature and precipitation and selected a copula distribution at each grid point. The copula enables construction of a time-varying multivariate distribution that models the dependence structure between warm and dry years at each grid point. Similar to the calculation of the probability of a warm (or a dry) anomaly in each year using the univariate distribution (described above), we used the multivariate copula distribution to quantify the joint probability of a temperature anomaly above the threshold and a precipitation anomaly below the threshold in each year, at each grid point. For the climate model analysis, we constructed the copula for each realization; e.g., in comparing the Historical and Natural experiments, we conducted the copula analysis individually for each realization for which temperature and precipitation data were both archived.
Given the importance of spatially co-occurring climate stresses [e.g., (3, 4)], we quantified the global probability of warm anomalies, dry anomalies, and warm+dry anomalies in each year by aggregating the respective warm, dry, and warm+dry probability values from the available grid points. In addition, we also calculated the joint probability of warm+dry anomalies simultaneously occurring in two regions. For this regional joint probability analysis, we first calculated the regional-mean temperature and precipitation time series for key crop and pasture regions (Fig. 3). Then, for each pair of regions, we constructed a four-dimensional C-vine copula (temperature in region 1, precipitation in region 1, temperature in region 2, and precipitation in region 2), which accounted for dependencies in the time series. We then used this four-dimensional copula to calculate the probability that both regions experienced warm+dry anomalies in the same year. We evaluated this joint probability of simultaneous warm+dry anomalies in pairs of regions for multidecadal periods of the historical observations, the Historical and Natural CMIP5 simulations, and the RCP2.6 and RCP8.5 CMIP5 simulations (see the Supplementary Materials for additional details).
Supplementary Material
Acknowledgments
We thank the editor and three anonymous reviewers for insightful and constructive comments. We thank NOAA’s NCEI for access to the observational temperature and precipitation data. We acknowledge the World Climate Research Programme’s Working Group on Coupled Modelling (which is responsible for CMIP), the climate modeling groups for producing and making available their model outputs, and U.S. Department of Energy (DOE)’s PCMDI for access to the CMIP5 data. Computational facilities were provided by CEES and SRCC at Stanford University. Funding: We acknowledge funding support from the DOE and Stanford University to N.S.D. M.P.W. acknowledges funding from the Spanish Government–Ministerio de Economía, Industria y Competitividad. M.C.A. acknowledges funding from the UC3M-BS Institute of Financial Big Data. Author contributions: N.S.D. proposed the idea of the work and supervised the research. A.S., M.C.A., and M.P.W. developed models. A.S. and D.T. collected data and performed spatial analyses. N.S.D. and A.S. drafted the first version of the manuscript. All authors were involved in discussions and editing the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. All data are available from the NOAA (https://www.ncdc.noaa.gov/temp-and-precip/ghcn-gridded-products/ and https://esgf-node.llnl.gov/projects/esgf-llnl/). Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/11/eaau3487/DC1
Section S1. Datasets
Section S2. Methodology
Fig. S1. Schematic flowchart of the methodology to calculate temporal probability of warm, dry, and warm+dry years.
Fig. S2. A C-vine copula with four dimensions, three trees, and six edges.
Fig. S3. P values for the time trend of the residual time series.
Fig. S4. Comparison of joint probability in the NOAA observations and CMIP5 Historical simulations.
Table S1. List of climate model realizations for temperature variable used to calculate warm year probability for the CMIP5 Historical and Natural forcing experiments and also for future projections based on RCP2.6 and RCP8.5.
Table S2. List of climate model realizations for precipitation variable used to calculate dry year probability for the CMIP5 Historical and Natural forcing experiments and also for future projections based on RCP2.6 and RCP8.5.
Table S3. List of climate model realizations available and overlapped for temperature and precipitation variables used to calculate joint warm and dry year probability for the CMIP5 Historical and Natural forcing experiments and also for future projections based on RCP2.6 and RCP8.5.
Table S4. Elliptical and Archimedean copula functions used in the present study.
REFERENCES AND NOTES
- 1.Intergovernmental Panel on Climate Change (IPCC), Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (Cambridge Univ. Press, 2012). [DOI] [PubMed] [Google Scholar]
- 2.IPCC, in Climate Change 2014: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, C. B. Field, V. R. Barros, D. J. Dokken, K. J. Mach, M. D. Mastrandrea, T. E. Bilir, M. Chatterjee, K. L. Ebi, Y. O. Estrada, R. C. Genova, B. Girma, E. S. Kissel, A. N. Levy, S. MacCracken, P. R. Mastrandrea, L. L. White, Eds. (Cambridge University Press, 2014), pp. 1–32. [Google Scholar]
- 3.Verma M., Hertel T., Diffenbaugh N., Market-oriented ethanol and corn-trade policies can reduce climate-induced US corn price volatility. Environ. Res. Lett. 9, 064028 (2014). [Google Scholar]
- 4.Ahmed S. A., Diffenbaugh N. S., Hertel T. W., Martin W. J., Agriculture and trade opportunities for Tanzania: Past volatility and future climate change. Rev. Int. Econ. 16, 429–447 (2012). [Google Scholar]
- 5.Tigchelaar M., Battisti D. S., Naylor R. L., Ray D. K., Future warming increases probability of globally synchronized maize production shocks. Proc. Natl. Acad. Sci. U.S.A. 115, 6644–6649 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ahmed S. A., Diffenbaugh N. S., Hertel T. W., Climate volatility deepens poverty vulnerability in developing countries. Environ. Res. Lett. 4, 034004 (2009). [Google Scholar]
- 7.Levermann A., Climate economics: Make supply chains climate-smart. Nature 506, 27–29 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Mills E., Insurance in a climate of change. Science 309, 1040–1044 (2005). [DOI] [PubMed] [Google Scholar]
- 9.Milly P. C. D., Betancourt J., Falkenmark M., Hirsch R. M., Kundzewicz Z. W., Lettenmaier D. P., Stouffer R. J., Stationarity is dead: Whither water management? Science 319, 573–574 (2008). [DOI] [PubMed] [Google Scholar]
- 10.Cheng L., AghaKouchak A., Gilleland E., Katz R. W., Non-stationary extreme value analysis in a changing climate. Clim. Change 127, 353–369 (2014). [Google Scholar]
- 11.Schölzel C., Friederichs P., Multivariate non-normally distributed random variables in climate research—Introduction to the copula approach. Nonlinear Process. Geophys. 15, 761–772 (2008). [Google Scholar]
- 12.Favre A.-C., El Adlouni S., Perreault L., Thiémonge N., Bobée B., Multivariate hydrological frequency analysis using copulas. Water Resour. Res. 40, 10.1029/2003WR002456 (2004). [Google Scholar]
- 13.Kwon H.-H., Lall U., A copula-based nonstationary frequency analysis for the 2012–2015 drought in California. Water Resour. Res. 52, 5662–5675 (2016). [Google Scholar]
- 14.Chebana F., Ouarda T. B. M. J., Multivariate quantiles in hydrological frequency analysis. Environ. Sci. Technol. 22, 63–78 (2011). [Google Scholar]
- 15.Mazdiyasni O., AghaKouchak A., Substantial increase in concurrent droughts and heatwaves in the United States. Proc. Natl. Acad. Sci. U.S.A. 112, 11484–11489 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zscheischler J., Seneviratne S. I., Dependence of drivers affects risks associated with compound events. Sci. Adv. 3, e1700263 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gallina V., Torresan S., Critto A., Sperotto A., Glade T., Marcomini A., A review of multi-risk methodologies for natural hazards: Consequences and challenges for a climate change impact assessment. J. Environ. Manage. 168, 123–132 (2016). [DOI] [PubMed] [Google Scholar]
- 18.Pereira G., Veiga Á., PAR(p)-vine copula based model for stochastic streamflow scenario generation. Stoch. Environ. Res. Risk Assess. 32, 833–842 (2018). [Google Scholar]
- 19.Zscheischler J., Westra S., van den Hurk B. J. J. M., Seneviratne S. I., Ward P. J., Pitman A., AghaKouchak A., Bresch D. N., Leonard M., Wahl T., Zhang X., Future climate risk from compound events. Nat. Clim. Change 8, 469–477 (2018). [Google Scholar]
- 20.Lesk C., Rowhani P., Ramankutty N., Influence of extreme weather disasters on global crop production. Nature 529, 84–87 (2016). [DOI] [PubMed] [Google Scholar]
- 21.Matiu M., Ankerst D. P., Menzel A., Interactions between temperature and drought in global and regional crop yield variability during 1961-2014. PLOS ONE 12, e0178339 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Diffenbaugh N. S., Hertel T. W., Scherer M., Verma M., Response of corn markets to climate volatility under alternative energy futures. Nat. Clim. Change 2, 514–518 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sadegh M., Ragno E., AghaKouchak A., Multivariate Copula Analysis Toolbox (MvCAT): Describing dependence and underlying uncertainty using a Bayesian framework. Water Resour. Res. 53, 5166–5183 (2017). [Google Scholar]
- 24.Sarhadi A., Soulis E. D., Time-varying extreme rainfall intensity-duration-frequency curves in a changing climate. Geophys. Res. Lett. 44, 2454–2463 (2017). [Google Scholar]
- 25.Sarhadi A., Ausín M. C., Wiper M. P., A new time-varying concept of risk in a changing climate. Sci. Rep. 6, 35755 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sippel S., Zscheischler J., Heimann M., Otto F. E. L., Peters J., Mahecha M. D., Quantifying changes in climate variability and extremes: Pitfalls and their overcoming. Geophys. Res. Lett. 42, 9990–9998 (2015). [Google Scholar]
- 27.Sippel S., Zscheischler J., Heimann M., Lange H., Mahecha M. D., J. van Oldenborgh G., Otto F. E. L., Reichstein M., Have precipitation extremes and annual totals been increasing in the world’s dry regions over the last 60 years? Hydrol. Earth Syst. Sci. 21, 441–458 (2017). [Google Scholar]
- 28.Vernieuwe H., Vandenberghe S., De Baets B., Verhoest N. E. C., A continuous rainfall model based on vine copulas. Hydrol. Earth Syst. Sci. 19, 2685–2699 (2015). [Google Scholar]
- 29.National Oceanic and Atmospheric Administration, GHCN gridded products (2018); www.ncdc.noaa.gov/temp-and-precip/ghcn-gridded-products/.
- 30.Taylor K. E., Stouffer R. J., Meehl G. A., An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 93, 485–498 (2012). [Google Scholar]
- 31.Le Quéré C., Andrew R. M., Canadell J. G., Sitch S., Korsbakken J. I., Peters G. P., Manning A. C., Boden T. A., Tans P. P., Houghton R. A., Keeling R. F., Alin S., Andrews O. D., Anthoni P., Barbero L., Bopp L., Chevallier F., Chini L. P., Ciais P., Currie K., Delire C., Doney S. C., Friedlingstein P., Gkritzalis T., Harris I., Hauck J., Haverd V., Hoppema M., Goldewijk K. K., Jain A. K., Kato E., Körtzinger A., Landschützer P., Lefévre N., Lenton A., Lienert S., Lombardozzi D., Melton J. R., Metzl N., Millero F., Monteiro P. M. S., Munro D. R., Nabel J. E. M. S., Nakaoka S., O’Brien K., Olsen A., Omar A. M., Ono T., Pierrot D., Poulter B., Rödenbeck C., Salisbury J., Schuster U., Schwinger J., Séférian R., Skjelvan I., Stocker B. D., Sutton A. J., Takahashi T., Tian H., Tilbrook B., van der Laan-Luijkx I. T., van der Werf G. R., Viovy N., Walker A. P., Wiltshire A., Zaehle S., Global carbon budget 2016. Earth Syst. Sci. Data. 8, 605–649 (2016). [Google Scholar]
- 32.N. Ramankutty, A. T. Evan, C. Monfreda, J. A. Foley, Global agricultural lands: Croplands, 2000 (2010); 10.7927/H4C8276G. [DOI]
- 33.Baillie R. T., Myers R. J., Bivariate garch estimation of the optimal commodity futures Hedge. J. Appl. Econ. 6, 109–124 (1991). [Google Scholar]
- 34.Sarhadi A., Burn D. H., Concepción Ausín M., Wiper M. P., Time-varying nonstationary multivariate risk analysis using a dynamic Bayesian copula. Water Resour. Res. 52, 2327–2349 (2016). [Google Scholar]
- 35.Gelman A., Rubin D. B., Inference from iterative simulation using multiple sequences. Stat. Sci. 7, 457–472 (1992). [Google Scholar]
- 36.Patton A. J., Modelling asymmetric exchange rate dependence. Int. Econ. Rev. (Philadelphia) 47, 527–556 (2006). [Google Scholar]
- 37.Aas K., Czado C., Frigessi A., Bakken H., Pair-copula constructions of multiple dependence. Insur. Math. Econ. 44, 182–198 (2009). [Google Scholar]
- 38.Sklar A., Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 8, 229–231 (1959). [Google Scholar]
- 39.Joe H., Families of m-variate distributions with given margins and m(m − 1)/2 bivariate dependence parameters. Lect. Notes Monogr. Ser. 28, 120–141 (1996). [Google Scholar]
- 40.Bedford T., Cooke R. M., Probability density decomposition for conditionally dependent random variables modeled by vines. Ann. Math. Artif. Intell. 32, 245–268 (2001). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/11/eaau3487/DC1
Section S1. Datasets
Section S2. Methodology
Fig. S1. Schematic flowchart of the methodology to calculate temporal probability of warm, dry, and warm+dry years.
Fig. S2. A C-vine copula with four dimensions, three trees, and six edges.
Fig. S3. P values for the time trend of the residual time series.
Fig. S4. Comparison of joint probability in the NOAA observations and CMIP5 Historical simulations.
Table S1. List of climate model realizations for temperature variable used to calculate warm year probability for the CMIP5 Historical and Natural forcing experiments and also for future projections based on RCP2.6 and RCP8.5.
Table S2. List of climate model realizations for precipitation variable used to calculate dry year probability for the CMIP5 Historical and Natural forcing experiments and also for future projections based on RCP2.6 and RCP8.5.
Table S3. List of climate model realizations available and overlapped for temperature and precipitation variables used to calculate joint warm and dry year probability for the CMIP5 Historical and Natural forcing experiments and also for future projections based on RCP2.6 and RCP8.5.
Table S4. Elliptical and Archimedean copula functions used in the present study.


