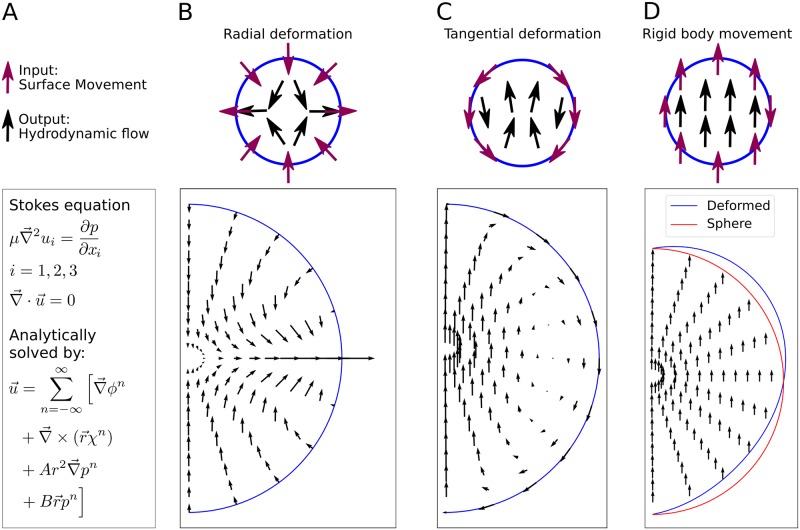
Fig 4. An analytical hydrodynamic calculation predicts flows from surface displacements.

A: The flows inside the oocyte are modelled as Stokes flows of an incompressible Newtonian fluid. We have constructed an analytical solution for the flows inside a moving sphere-like boundary. We applied it to the flows inside a rotationally symmetric object. The problem reduces to the calculation of three fields ϕ, χ and p from the surface movement as given in the Methods section. B: The model predicts the flows for arbitrary radial surface movement, exemplified here by a surface movement where there is influx at the poles and outflux at the equator. C: Arbitrary tangential surface movement can be included, exemplified by constant surface movement from one pole to another. D: Due to linearity of the Stokes equation different contributions to the flows can be separately calculated and added up so that rigid body movement can be predicted from adding up radial and tangential flows. The model is extended using perturbation theory to also deal with non-spherical shapes. This is exemplified by rigid body movement of a deformed sphere (blue). An undeformed sphere is shown as reference (red).