Kinetic Analysis of Enzymes Immobilized in Porous Film Arrays

Abstract

Measuring the catalytic activity of immobilized enzymes underpins development of biosensing, bioprocessing, and analytical chemistry tools. To expand the range of approaches available for measuring enzymatic activity, we report on a technique to probe activity of enzymes immobilized in porous materials in the absence of confounding mass transport artifacts. We measured reaction kinetics of calf intestinal alkaline phosphatase (CIAP) immobilized in benzophenone-modified polyacrylamide (BPMA-PAAm) gel films housed in an array of fluidically isolated chambers. To ensure kinetics measurements are not confounded by mass transport limitations, we employed Weisz’s modulus (Φ), which compares observed enzyme-catalyzed reaction rates to characteristic substrate diffusion times. We characterized activity of CIAP immobilized in BPMA-PAAm gels in a reaction-limited regime (Φ ≪ 0.15 for all measurements), allowing us to isolate the effect of immobilization on enzymatic activity. Immobilization of CIAP in BPMA-PAAm gels produced a ~2× loss in apparent enzyme–substrate affinity (K_m) and ~200× decrease in intrinsic catalytic activity (k_cat) relative to in-solution measurements. As estimating K_m and k_cat requires multiple steps of data manipulation, we developed a computational approach (bootstrapping) to propagate uncertainty in calibration data through all data manipulation steps. Numerical simulation revealed that calibration error is only negligible when the normalized root-mean-squared error (NRMSE) in the calibration falls below 0.05%. Importantly, bootstrapping is independent of the mathematical model, and thus generalizable beyond enzyme kinetics studies. Furthermore, the measurement tool presented can be readily adapted to study other porous immobilization supports, facilitating rational design (immobilization method, geometry, enzyme loading) of immobilized-enzyme devices.

Enzyme immobilization on solid supports has fueled advances in biosensing,^1,2 biocatalysis,³ and proteomics,^4,5 among other fields. The history, applications, and available methods of enzyme immobilization are vast, as covered in various reviews.^6–12 Key design parameters (i.e., immobilization method, device geometry, and enzyme loading) determine performance (e.g., sensor dynamic range, reactor yield) of devices employing immobilized enzymes. As suggested by Nidetzky and colleagues, design should be guided by characterization of immobilized enzymes at multiple length scales starting with kinetics measurements.¹³ Yet, kinetics of immobilized enzymes are often studied only after device development. Although the use of immobilized enzymes for biosensing, analytical chemistry, and bioprocessing applications has increased, methods to characterize the kinetics of immobilized enzymes^14,15 remain similar to those proposed by Engasser and Horvath in 1973.¹⁶ As applications benefiting from immobilized enzymes expand, the availability of diverse methods to characterize the kinetics of immobilized enzymes is increasingly important.

In contrast to kinetics measurements of enzymes in free solution, immobilized enzyme reactions do not necessarily occur under spatially uniform substrate^16,17 and pH distributions.^17,18 In porous materials, partitioning and mass transport limitations may yield spatial variation in local reaction rates, obscuring determination of the true kinetics of the immobilized enzyme.^16–18 Further, immobilization can alter the intrinsic kinetics of the enzyme by changing enzyme structure and local microenvironment.^19–21 To isolate the effect of immobilization on the catalytic activity of an enzyme, confounding factors must be evaluated.

Immobilization often improves enzyme stability at the cost of lower catalytic activity.¹² However, strategic selection of enzyme immobilization methods may mitigate losses or increase activity upon immobilization.^12,22,23 For example, immobilization of enzymes in highly activated supports can promote multipoint covalent attachment (MCA), restricting the enzyme from adopting inactive conformations post-immobilization.²⁴ Similarly, choice of enzyme loading and immobilization matrix can favor partitioning of H⁺ or OH⁻ ions, altering the local pH in the support material relative to the bulk. The changed pH may allow the immobilized enzyme to operate in conditions closer to the optimal pH.²⁵ The conformation of the enzyme at the time of immobilization can also affect its activity. MCA immobilization of lipases in the presence of detergents can increase activity as the enzyme is immobilized in an active conformation.²⁶ Immobilization mechanism and selected protocol can both have profound effects on the performance of immobilized enzymes, and thus require characterization on a case-by-case basis.

Omission of standard enzymatic activity metrics (e.g., K_m, V_max, k_cat)²⁷ or derivation of apparent activity metrics from data sets other than reaction progress curves²⁸ can preclude utilization of published literature to guide rational selection of immobilization schemes. To improve meaningful comparisons across enzyme kinetics studies, minimal reporting standards (i.e., STRENDA) have been published, which include aspects of model selection and error analysis.^29,30 The latter is of particular interest because K_m, V_max, and k_cat are not directly measurable properties, but rather are estimated from fitting the Michaelis–Menten model to initial reaction rates measured at several substrate concentrations, [S]. As a result, estimating K_m, V_max, and k_cat in standard units requires: (i) calibration correction of the raw reaction progress data, (ii) linear regression to estimate initial reaction rates from calibration-corrected data, and (iii) nonlinear fitting of the Michaelis–Menten model to the initial reaction rate estimates as a function of [S]. The sequential calculations utilized to estimate Michaelis–Menten model parameters make propagation of uncertainty techniques important in enzyme kinetics studies.

Computational methods are practical alternatives to the derivation of analytical solutions for error propagation. While more computationally intensive than its predecessor (i.e., the jackknife), bootstrapping is a versatile data resampling technique for estimating uncertainty in calculated parameters.^31,32 Furthermore, in contrast to the jackknife,³³ bootstrapping can be applied to calibration experiments.^34,35 Bootstrapping generates “pseudo-samples,” or bootstrap samples, size-matched to the original data set by sampling with replacement from the original data. Parameters of interest (e.g., K_m, V_max, k_cat) are calculated from each bootstrap sample, yielding a distribution of parameters, whose standard deviation approximates the standard error (uncertainty) in the parameter. Crucially, bootstrapping does not require exact mathematical expressions for the uncertainty, offering a practical method to estimate uncertainty in Michaelis–Menten model parameters. Applied to biological assays, Hanson et al.³⁶ and Blukacz et al.³⁷ used bootstrapping simulations to propagate systematic measurement error (e.g., pipetting/caliper accuracy) onto estimates of enzyme inhibitor potency and biomass production, respectively. Furthermore, bootstrapping methods, which focused exclusively on the final step of data analysis, have been used to estimate uncertainty in K_m and V_max^38,39 Therefore, a bootstrapping strategy to propagate calibration uncertainty onto the K_m, V_max, and k_cat estimates would be useful to study kinetics of immobilized and free enzymes.

In biological systems, enzymatic activity is regulated through multiple mechanisms; thus, protein abundance measurements (e.g., Western blotting) are insufficient to investigate the role of enzymes in complex biological networks.⁴⁰ Building on our group’s microscale electrophoretic assays in benzophenone-modified polyacrylamide (BPMA-PAAm) gels,^41–43 we sought to understand the feasibility of quantifying both protein abundance and enzymatic activity from single cells. Here, we introduce an analytical method suitable for ascertaining the impact of immobilization in BPMA-PAAm gels on the enzymatic activity of calf intestinal alkaline phosphatase (CIAP). Our two-component system comprises (i) a thin, microfabricated hydrogel film for enzyme immobilization mounted on (ii) a gasket fixture defining an array of fluidically isolated hydrogel regions compatible with a standard microplate reader. We evaluate the validity of primary assumptions of the Michaelis–Menten model and utilize a quantitative framework to assess the presence of mass transport limitations based on measurable properties. We find that our enzyme kinetics measurements occur in a reaction-limited regime, allowing us to estimate intrinsic k_cat values for CIAP immobilized in BPMA-PAAm gels. In addition, we describe a bootstrapping method to propagate uncertainty in each step of data analysis onto the final K_m, V_max, and k_cat estimates and investigate conditions for which calibration uncertainty is non-negligible. As bootstrapping is independent of the mathematical model, the error propagation approach can be readily modified for applications other than Michaelis–Menten kinetics. Similarly, our measurement system can be utilized to investigate the performance of other porous materials for enzyme immobilization.

EXPERIMENTAL SECTION

Chemicals/Reagents.

Acetic acid (695092), methanol (322415), 3-(trimethoxysilyl)propyl methacrylate (440159), 40% T, 3.3% C acrylamide/bis-acrylamide (29:1) (A7802), N,N,N′,N′-tetramethylethylenediamine (TEMED, T9281), ammonium persulfate (APS, A3678), sodium dodecyl sulfate (SDS, L3771), 2-mercaptoethanol (M3148), zinc chloride (ZnCl₂, 208086), and sodium chloride (NaCl, S9888) were purchased from Sigma-Aldrich. 6,8-Difluoro-4-methylumbelliferyl phosphate (DiFMUP, 6567), 6,8-difluoro-7-hydroxy-4-methylcoumarin (DiFMU, 6566), ELF97 endogenous phosphatase detection kit (ELF97 substrate and reaction buffer, E6601), ELF97-alcohol (E6578), biotinylated calf intestinal alkaline phosphatase (CIAP, E.C. 3.1.3.1, Cat. No. 29339), AlexaFluor488 labeling kit (A20181), and hydrochloric acid (A144S) were acquired from Thermo Fisher Scientific. Tris-buffered saline with Tween (20X TBST, 281695) and Tris base (3715-A) were procured from Santa Cruz Biotechnology. 0.5 M Tris-HCl pH 6.8 was obtained from Teknova (T1568). Magnesium chloride hexahydrate (MgCl₂·6H₂O, 5580) was purchased from EMD Chemicals. Deionized water (18.2 MΩ) was obtained using an Ultrapure water system from Millipore. N-[3-[(3-Benzoylphenyl)-formamido]propyl]methacrylamide (BPMA) was custom synthesized by PharmAgra.

Fluorescent Protein Calibration.

All gels in this study were fabricated using an SU-8 mold with ~43 μm tall features measured with a surface profilometer (Sloan Dektak 3030). CIAP was labeled with AlexaFluor488 according to manufacturer’s instructions. Immediately prior to fabricating flat BPMA-PAAm gels (8%T, 3.3%C, 3 mM BPMA comonomer) without microwell features as described previously,^44,45 fluorescently labeled CIAP (CIAP*) was added to gel precursor solutions in known concentrations. After fabrication, the gels were exposed to UV light using a collimated mercury lamp (~20 mW/cm² at 365 nm, Optical Associates, Inc.) for 5 min and allowed to air-dry overnight. Fluorescence from the dry gels was measured with a laser microarray scanner (Genepix 4300A, Molecular Devices). Mean fluorescence intensity of select ~42 mm² gel regions was used to construct a calibration curve (n = 25 regions per concentration).

Selective Protein Introduction.

BPMA-PAAm gels were fabricated as described, and stored in 1× TBST at 4 °C. Prior to use the gels were dried under a N₂ stream, and mounted on gasket fixtures (AHC1 × 16, ArrayIt Inc.), creating 8 × 2 arrays of independent 42.3 ± 0.1 mm² gel regions (Figure 1A). The gel regions were rehydrated in 1× TBST for ~20 min, followed by incubation with freshly prepared 250 nM solutions of CIAP or CIAP* in 1× TBST. After incubation for 2 h under a dark cover at room temperature (RT), the gasket fixtures were exposed to UV light as described above. After UV exposure, each gel region was rinsed with fresh 1× TBST followed by disassembly of the gasket fixtures. To remove unbound enzyme, the gels were washed overnight in 1× TBST at RT with mild agitation under a dark cover. To estimate concentration of CIAP in each gel region, CIAP*-containing gels were dried under a N₂ stream and mean fluorescence of each ~42 mm² region was measured as described above (n = 12 gel regions). To investigate immobilization uniformity, we calculated coefficients of variation (CV) for all the pixels in each ~42 mm² region. The mean CV for all regions was 7.5 ± 1.3%, suggesting CIAP* is uniformly immobilized in each ~42 mm² region. For kinetics experiments, the gels were dried under a N₂ stream and remounted on the gasket fixtures. Each enzyme-containing gel region was rehydrated in 1× TBST at RT for ~20 min prior to use.

Figure 1.

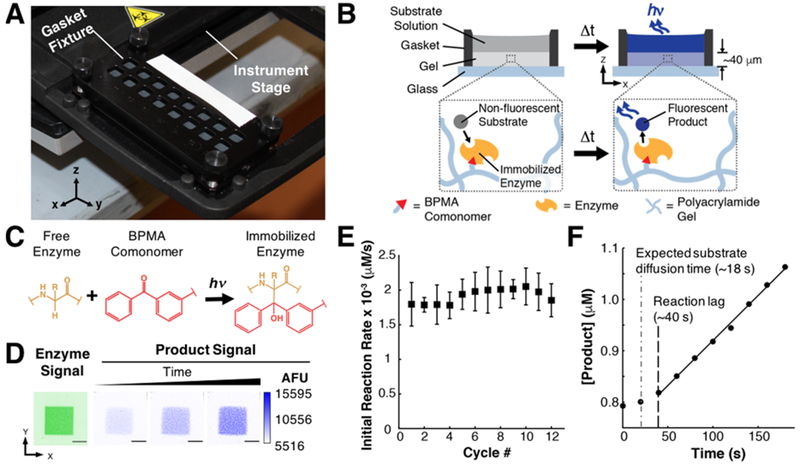
Measuring kinetics of enzymes immobilized in thin hydrogel film arrays. (A) Photograph of gasket fixture defining an array of ~42 mm² gel regions mounted on a microplate reader stage. (B) Cross-sectional schematic of a single gel region containing covalently immobilized enzyme fluidically isolated from adjacent regions by the gasket fixture. During the immobilization process, the gasket fixture holds a concentrated enzyme solution. After immobilization, the gasket fixture is reassembled and filled with substrate solution for kinetics measurements. (C) Enzymes are immobilized in BPMA-PAAm gels through the N-[3-[(3-benzoylphenyl)-formamido]propyl]methacrylamide (BPMA) comonomer upon exposure to UV light. (D) Inverted fluorescence micrographs illustrate colocalization of fluorescent product of enzyme-catalyzed dephosphorylation of ELF97 substrate with regions of gel containing fluorescently labeled immobilized CIAP (scale bar = 0.5 mm). (E) CIAP covalently immobilized in BPMA-PAAm gels retains catalytic activity through multiple cycles of exposure to fresh DiFMUP (50 μM) substrate solutions, indicating the immobilized CIAP is stable through enzyme kinetics measurements. Error bars indicate one standard deviation of mean initial reaction rate measurements (n = 8 initial reaction rate measurements per cycle). (F) Following an initial lag period, CIAP-catalyzed dephosphorylation of DiFMUP is linear (R² > 0.99), which is consistent with the steady-state assumption of the Michaelis-Menten model.

Immobilized Enzyme Kinetics Measurements.

To evaluate stability and kinetics parameters of CIAP immobilized in BPMA-PAAm gels, fluorescent emission at 448 ± 10 nm of DiFMU upon CIAP-catalyzed dephosphorylation of DiFMUP was measured at 20 s intervals for 3 min with 374 ± 4.5 nm excitation and orbital agitation (28.8 rpm) between measurements on a microplate reader (Tecan Infinite M200 Pro). All kinetics measurements were conducted in pairs of adjacent gel regions at RT. Rehydrating 1× TBST was aspirated from the CIAP-containing gel while the gasket fixture was secured on the measurement stage of the instrument with double-sided tape. DiFMUP solutions, prepared in 100 mM Tris, 150 mM NaCl, 50 mM MgCl₂, 0.1 mM ZnCl₂ buffer titrated to pH 7.8 with HCl, were then added over the CIAP-containing gel regions prior to starting the measurements. To generate the fluorescent product calibration curve, fluorescence of DiFMU solutions prepared in the indicated buffer was measured in enzyme-free gel regions (n = 7 solutions per concentration). Formation of fluorescent precipitates upon CIAP-catalyzed dephosphorylation of ELF97 was measured every 2 min with 500 ms exposures at 4 × 4 pixel binning through a 4× magnification objective (Olympus UPlanFLN, NA 0.13) on an Olympus IX71 inverted fluorescence microscope equipped with an Andor iXon + EMCCD camera, shuttered mercury lamp (X-Cite, Lumen Dynamics), and a DAPI long pass emission filter cube (Omega XF02–2). Solutions of ELF97 (250 μM) were prepared in manufacturer-provided reaction buffer and complemented with 5 μM ELF97-alcohol. We reused the silicone gaskets on the gasket fixtures for selective protein loading and kinetics measurements. Critical to eliminating unwanted variability due to residual activity from CIAP retained on the silicone gaskets, we washed the gaskets in a 0.5 M Tris-HCl pH 6.8, SDS (2% w/v), 2-mercaptoethanol (0.8% v/v) buffer at 55 °C for ~1 h⁴⁴ prior to starting kinetics measurements (Figure S1).

Estimates of Parameters and Uncertainties.

Existing functions in MATLAB R2015a were used to calculate calibration parameters, initial reaction rates, and Michaelis–Menten model parameters. Linear least-squares regression (y = mx + b) was used to generate calibration curves and to estimate initial reaction rates from kinetics measurements. For calibration, regressions were weighted according to the reciprocal of the variance (1/σ²) of replicate measurements at each concentration. Nonlinear least-squares regression of the Michaelis–Menten model $(v([\text{S}])=\frac{V_{\max }[\text{S}]}{K_{\mathrm{m}}+[\text{S}]})$ to initial reaction rates measured at several [S] was used to estimate K_m and V_max. Two methods were used to estimate uncertainty in each parameter.

Conventional Method.

The regression functions return estimates of the fit parameters including 95% confidence intervals for each parameter of the form:

$$\text{parameter estimate}\pm t\cdot S_e$$ (1)

where S_e is the standard error in the fit parameter and t is the critical t-value for P > 0.05. Appropriate t-values were extracted from available tables⁴⁶ to calculate S_e for each fit parameter. For uncertainty in K_m and V_max, this method assumes negligible uncertainty in the product calibration data as S_e only accounts for uncertainty in fitting the Michaelis–Menten model to the initial reaction rate data.

Bootstrapping Method.

To propagate uncertainty in the product calibration data onto the final estimates K_m, V_max, and k_cat, we adapted the bootstrapping method described by Jones et al.^34,35 for calibration experiments. We implement the approach in three stages: (i) calibration correction, (ii) initial reaction rate calculation, and (iii) fitting the Michaelis–Menten model. Additional details are provided in the included Supporting Information.

Calibration Correction.

Bootstrap samples size-matched to the original calibration data set (n = 35) were generated from a pool of adjusted normalized residuals to the weighted linear regression fit by sampling with replacement. A new calibration curve was generated from each bootstrap sample of residuals, which produced distributions of calibration slope and intercept parameters. Each bootstrap calibration curve was applied to each point of the original kinetics measurements, producing a set of calibration-corrected kinetics data sets.

Initial Reaction Rate Calculation.

For each time point, bootstrap samples of calibration-corrected kinetics data were generated by sampling with replacement from the calibration-corrected kinetics data sets. The initial reaction rate for each bootstrap sample of calibration-corrected kinetics data was determined, resulting in a distribution of initial reaction rate values for each set of original kinetics data sets.

Fitting the Michaelis–Menten Model.

Bootstrap samples size-matched to the original set of kinetics measurements (n = 64) were generated from a pool of adjusted normalized residuals to the mean initial reaction rate for each set of original kinetics measurements. The Michaelis–Menten model was fitted to each new set of initial reaction rates as a function of [S], generating distributions of K_m and V_max. The uncertainty in each term is reported as one standard deviation of the mean of each distribution.

RESULTS AND DISCUSSION

Measuring Kinetics of Enzymes Immobilized in Gels.

Immobilized enzymes follow the Michaelis–Menten model,^16,17 which relates the initial rate of the enzyme-catalyzed reaction to the substrate concentration, [S]. The model parameters, K_m and V_max, are descriptors of enzymatic activity. Key assumptions must hold to ensure the validity of the Michaelis–Menten model during the course of kinetics measurements, namely: (i) the enzyme is stable and (ii) substrate concentration is at steady-state $\left(\frac{\mathrm{d}\left[\mathrm{S}\right]}{\mathrm{d}t}\approx 0\right)$. However, even when these assumptions are met, the true (intrinsic) kinetics of an enzyme immobilized in a porous matrix may be obscured by partitioning behavior and mass transport limitations.^16,17 In this study, we sought to measure the catalytic activity of enzymes immobilized in hydrogels that may be subject to both partitioning and mass transport limitations. Our system is an alkaline phosphatase, a well-characterized^47–49 and important marker of stem cell pluripotency,^50–52 immobilized in a polyacrylamide gel matrix (BPMA-PAAm) through benzophenone-mediated covalent attachment. We aimed to determine K_m and k_cat, which are independent of enzyme concentration, and thus directly comparable to in-solution controls. As $k_{\mathrm{cat}}=\frac{V_{\max }}{\left[E_{\mathrm{T}}\right]},$ estimating k_cat requires measuring the in-gel enzyme concentration, [E_T]. The modular measurement system reported here allows for (i) quantitation of immobilized enzyme concentration, (ii) validity assessment of Michaelis–Menten model assumptions, and (iii) evaluation of the effects of confounding factors on the observed kinetics, as detailed in the following sections.

Quantifying In-Gel Enzyme Concentration.

First, we developed a method to immobilize CIAP in independent regions (42.3 ± 0.1 mm²) of preformed BPMA-PAAm gels using a gasket fixture (Figure 1A and B). Upon exposure to UV light, the BPMA comonomer in the gel forms covalent C–C bonds with proteins through a hydrogen-abstraction and radical recombination process (Figure 1C).^53,54 Every α-carbon on the polypeptide backbone is a suitable candidate for H-abstraction;^53,54 thus, enzyme molecules are preferably immobilized in BPMA-PAAm gels through covalent bonds anywhere along the enzyme backbone (Figure 1C). As a result, the conformation of the enzyme may be affected upon immobilization, and the orientation of the catalytic sites relative to the support matrix was not controlled in our study. To verify that CIAP remained catalytically active upon covalent attachment to the gel matrix, we immobilized fluorescently labeled CIAP (CIAP*) through a photomask with 1 mm² slits (Figure 1D) and exposed the enzyme-containing gel to a precipitating substrate, ELF97. The normally soluble, nonfluorescent ELF97 substrate forms insoluble, fluorescent precipitates upon CIAP-catalyzed dephosphorylation.⁵⁵ Co-localization of fluorescent ELF97 precipitates in the 1 mm² gel regions containing CIAP* (Figure 1D) indicated the immobilized enzyme retained catalytic activity and that the reaction occurred in the gel. To quantify the amount of CIAP* immobilized in the gel by this method, we fabricated a set of BPMA-PAAm gels containing known amounts of CIAP*, and measured fluorescence as a function of [CIAP*] to generate a calibration curve (y = 4108.1x + 6547.0, R² = 0.96). On the basis of the calibration results, the estimated [CIAP*] immobilized in each independent gel region was 1.7 ± 0.2 nM. Since CIAP is a dimeric protein, the total concentration of catalytic sites immobilized in each gel region was 3.4 ± 0.4 nM. Direct and independent quantitation of immobilized CIAP overcomes some of the limitations of previous reports, which estimate the concentration of immobilized CIAP based on theoretical estimates of surface coverage^47–49 or activity measurements assuming the immobilization process does not alter enzymatic activity.²⁷ Furthermore, the effects of thermodynamic partitioning⁵⁶ and covalent immobilization efficiency^41,57,58 can be harnessed to tune the concentration of immobilized enzyme, [C_immobilized] (Figure S2). As each enzyme-containing gel region is fluidically isolated, multiple [C_immobilized] can be tested in parallel to determine the [C_immobilized] range required to operate without confounding mass transport limitations.

Assessing Validity of Michaelis–Menten Model Assumptions.

As the Michaelis–Menten model is only valid if the enzyme remains stable through the measurement period, we sought to evaluate the stability of CIAP immobilized in BPMA-PAAm gels. Losses in enzyme stability produce losses in catalytic activity and concomitant decreases in enzyme-catalyzed reaction rates.⁵⁹ As the enzyme is covalently attached to the gel, we hypothesized that decreases in enzyme-catalyzed reaction rates are caused solely by losses in enzyme stability as opposed to enzyme losses. We based this assumption on our previous reports demonstrating that proteins can be immuno-detected in BPMA-PAAm gels even after exposure to high temperature (~55 °C),^41,60 ionic detergents,^41,60 reducing agents,^41,60 and strong acids.⁴² To evaluate the stability of CIAP covalently bound to BPMA-PAAm gels, we cyclically exposed CIAP-containing gel regions to fresh 50 μM solutions of DiFMUP and monitored formation of fluorescent product for 3 min followed by a 10 min wash between measurement cycles. We compared the mean rates of fluorescent product formation across 12 cycles of exposure to the substrate using one-way ANOVA, which indicated the mean rates were statistically equivalent (P > 0.05) across cycles (Figure 1E). Consequently, we conclude that CIAP covalently attached to BPMA-PAAm gels is stable over the course of the single initial reaction rate measurements utilized for enzyme kinetics experiments. Further investigations of long-term (e.g., days, months) stability of enzymes immobilized in BPMA-PAAm gels are still required to determine the utility of this material for biosensor applications.

The second assumption for Michaelis-Menten model validity is that concentration of substrate remains approximately constant during the measurement period $(\frac{\mathrm{d}\left[\mathrm{S}\right]}{\mathrm{d}t}\approx 0)$. To evaluate this assumption, we characterized the linearity of the enzyme-catalyzed reaction with respect to time. Since, according to the Michaelis–Menten model, the initial rate of the enzyme-catalyzed reaction is directly proportional to the substrate concentration, departures from linearity could be indicative of substrate depletion $(\frac{\mathrm{d}\left[\mathrm{S}\right]}{\mathrm{d}t}\ne 0)$, product inhibition, or both. We measured the rate of formation of fluorescent DiFMU upon CIAP-catalyzed dephosphorylation of DiFMUP, fitted a linear model to the kinetics data, and utilized the coefficient of determination (R²) as a metric of linearity. CIAP-catalyzed formation of fluorescent DiFMU exhibited linear behavior after an initial lag period with R² ≥ 0.98 in 158 of the 160 kinetics measurements conducted in this study (Figure 1F). Given the linearity of the rate of formation of DiFMU with respect to time, we conclude that the substrate steady-state condition $(\frac{\mathrm{d}\left[\mathrm{S}\right]}{\mathrm{d}t}\approx 0)$ holds during the course of the measurements.

We observed lag periods (~40 s) considerably longer than the expected diffusion equilibration time for DiFMUP (Figure 1F). The estimated diffusion equilibration time of DiFMUP through the gel thickness (τ ≈ L²D⁻¹) was ~18 s, where L is the height of the gel (43 μm) and D (10⁻⁶ cm²/s) is a conservative estimate of the diffusivity of DiFMUP based on reported values for small molecules (≤ 340 Da) in 9.5% T polyacrylamide gels.⁶¹ The discrepancy arises as the local concentration of DiFMUP in the gel simultaneously depends on the rate of diffusive transport from the bulk into the gel and the rate of substrate consumption due to the enzyme-catalyzed reaction. Therefore, the lag coincides with a transient period preceding a local steady-state in which the local concentration of DiFMUP in the gel reaches a constant value. As prescribed by the Michaelis–Menten model, the local rate of the enzyme-catalyzed reaction becomes constant when the local concentration of substrate in the gel also reaches a constant value. Meeting the local steady-state condition is contingent upon minimal changes in the bulk substrate concentration during the measurement period, which ensure the diffusive flux of substrate into the gel remains constant. Establishing a steady-state in the local substrate concentration in the gel, however, is not synonymous with a spatially uniform substrate concentration in the gel.^16,17 As a result, the linearity of our experimental data indicates that the local substrate concentration is temporally invariant during the measurement but offers little information about the spatial distribution of substrate within the gel, as discussed next.

Evaluating Effects of Partitioning and Mass Transport Limitations on Observed Kinetics.

The true kinetics of the immobilized catalyst may be confounded by variation in the local, in-gel substrate concentration^16,17 and in-gel pH.^17,18 Partitioning, (external) diffusion of the substrate to the liquid-hydrogel interface, and (internal) diffusion of the substrate within the porous support may alter the effective concentration of substrate in contact with the immobilized enzyme.^16–18 Partitioning in porous matrices occurs when enrichment of the solute in either the liquid or solid phase is thermodynamically favorable. Electrostatic interactions between solutes (i.e., substrate, hydrogen ions) and the porous support can drive partitioning to alter the local substrate concentration or pH.^16–18 While fixed negative charge in polyacrylamide gels has been reported,⁶² the high ionic strength of the buffer in this study is expected to mitigate electrostatically driven partitioning of the substrate and/or hydrogen ions into the gel.^16–18 Similarly, hydrophobic interactions may drive substrate partitioning, causing the apparent (observed) K_m to differ from the intrinsic K_m of the immobilized enzyme.^17,18 If necessary, intrinsic K_m values could be estimated as the product of the apparent K_m and the substrate partitioning coefficient, provided that accumulation of product in the support matrix and diffusional limitations are negligible.⁶³

External diffusion limitations arise when the rate of the enzyme-catalyzed reaction at the surface of the porous matrix greatly exceeds the rate of transport of substrate to the surface.^16,17 In the absence of convective flow, external diffusion limitations produce a diffusion boundary layer of lower substrate concentration than the bulk. Coupling the gasket fixture with a microplate reader allowed us to make multiple kinetics measurements simultaneously, but prevented us from stirring the substrate solution above each ~42 mm² gel region through conventional means (e.g., magnetic stir bars). Instead, we used the orbital shaking function of the instrument to agitate the gasket fixture between consecutive measurements to prevent formation of diffusion boundary layers, and thus mitigate external diffusion limitations on the observed kinetics. Therefore, we assume external diffusion limitations are negligible and focus our analysis on the effect of internal diffusion on the observed kinetics.

Internal diffusion limitations arise when the rate of diffusive transport of substrate in the solid is significantly slower than the rate of the enzyme-catalyzed reaction.^16,17 As a result, the immobilized catalyst may be exposed to varying concentrations of substrate depending on its location within the support material. Thus, the local rate of the enzyme-catalyzed reaction may vary throughout the solid support. Since direct measurements of the local rate of the enzyme-catalyzed reaction are impractical, aggregate (global) rates are employed to study the kinetics of immobilized enzymes. In the presence of internal diffusion limitations, however, the global rate measurements may underestimate the true catalytic potential of the immobilized enzyme. k_cat values derived from experimental data subject to internal diffusion limitations fail to capture the intrinsic activity of the immobilized enzyme, and thus are not comparable to other systems or to in-solution experiments.

To evaluate the presence and severity of internal diffusion limitations on global reaction rate measurements, we employed Weisz’s modulus (Φ).^64,65 The dimensionless number Φ is estimated from measurable quantities relating the rate of the reaction to the rate of diffusive transport of the substrate in the solid support.64,65 Roberts et al.⁶⁶ found that for reactions following the Michaelis–Menten model and occurring in slab-shaped solid supports, Φ could be defined as

$$\Phi =\frac{L^2{v}_{\mathrm{obs}}}{D{S}_{\mathrm{o}}}$$ (2)

where L is the characteristic length, v_obs is the global reaction rate measured at bulk substrate concentration S_o, and D is the diffusivity of the substrate in the support matrix. Internal diffusion limitations are considered negligible when Φ < 0.15, indicating the system operates in a reaction-limited regime and the in-gel substrate concentration is spatially uniform.^64,66 Substituting L and D values mentioned above and mean v_obs for each concentration tested, we obtained Φ ≪ 0.15. Consequently, we conclude that limitations imposed by partitioning, external diffusion, and internal diffusion do not result in spatial variation in local reaction rates, allowing us to isolate the effect of benzophenone-mediated immobilization on the apparent enzyme–substrate affinity (K_m) and intrinsic catalytic activity (k_cat) of CIAP. While intrinsic k_cat cannot be determined directly if Φ > 0.15, effectiveness factor analysis can be utilized to estimate intrinsic values.^18,64 Once intrinsic k_cat and apparent K_m values are determined, v_obs can be estimated from the Michaelis–Menten model for different enzyme concentrations, and L values optimized to meet a threshold Φ condition. The optimization approach described above is equivalent to diffusion distance reduction and enzyme loading minimization strategies common to small particle systems.^14–16 However, studying enzymes immobilized in adherent films eliminates particle damage from aggressive stirring⁶⁷ and facilitates integration with confocal microcopy methods.^68–70 The latter is the subject of future work to study the spatial distribution of enzyme, substrate, or pH in the support matrix. Taken together, we offer a quantitative framework to characterize the kinetics of immobilized enzymes and subsequently guide rational design choices (e.g., enzyme loading, geometry) for immobilized-enzyme devices.

Kinetics of Immobilized Calf Intestinal Alkaline Phosphatase.

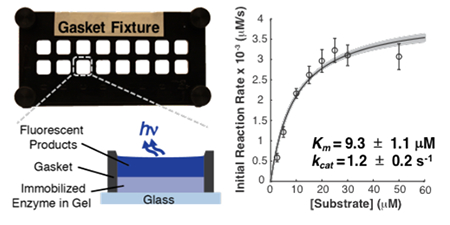
We next scrutinized the kinetics of CIAP-catalyzed dephosphorylation of DiFMUP in the hydrogel reactor. To estimate apparent K_m and intrinsic k_cat for CIAP immobilized in BPMA-PAAm gels, we exposed individual gel regions to DiFMUP solutions (2.5–50 μM) and measured formation of fluorescent product with respect to time. Subsequently, we fitted the Michaelis–Menten model to the initial reaction rate data to extract estimates of K_m, V_max, and k_cat (Table 1). We completed a control experiment for CIAP in solution to compare the kinetics of the immobilized enzyme relative to the free enzyme (Figure S3). Upon benzophenone-mediated attachment of CIAP in thin BPMA-PAAm gel films, we observed a ~2× increase in the apparent K_m relative to CIAP in solution, which suggests lower affinity of the immobilized CIAP for DiFMUP. Similarly, the ~200× decrease in intrinsic k_cat relative to CIAP in solution suggests that immobilization of CIAP in BPMA-PAAm gels reduces catalytic activity. The losses in enzyme–substrate affinity and enzymatic activity are consistent with previous studies of alkaline phosphatase immobilized on surfaces via biotin–streptavidin linkers relative to free solution measurements.^47–49 However, direct comparisons are confounded by differences in immobilization methods and differences between the catalytic activity of enzymes bound to a surface as opposed to a porous matrix. We hypothesize that the losses in apparent enzyme–substrate affinity and intrinsic catalytic activity upon immobilization in BPMA-PAAm gels result from random orientation of the catalytic sites relative to the solid supports,²⁰ changes in enzyme conformation and molecular mobility,²¹ and local microenvironment conditions.¹⁹ Next, we explore a computational method to estimate the uncertainty in the reported K_m, V_max, and k_cat.

Table 1.

Estimates of Michaelis–Menten Model Parameters for Immobilized and Free Calf Intestinal Alkaline Phosphatase

	conventional estimates			bootstrap estimates
condition	Km (μM)	kcat(s−1)a	Vmax (nM/s)	Km (μM)	kcat(s−1)a	Vmax (nM/s)
immobilized	9.3 ± 1.1	1.2 ± 0.2	4.1 ± 0.2	9.3 ± 0.3	1.2 ± 0.1	4.1 ± 0.05
in-solution	5.3 ± 0.7	230.2 ± 12.5	106.8 ± 3.5	5.3 ± 0.4	229.7 ± 11.5	106.6 ± 2.7

^a[CIAP_immobilizedl = 3.4 ± 0.4 nM. [CIAP_in-solution] = 0.464 ± 0.02 nM.

Bootstrapping Method for Error Propagation.

We were interested in understanding the effect of calibration error on the final uncertainty estimates of K_m, V_max, and k_cat values. However, to our knowledge, analytical solutions to propagate calibration error onto the final estimates of Michaelis–Menten parameters have not been published, and our attempts at deriving analytical solutions quickly became intractable. Since propagation of uncertainty through multiple data manipulation steps is not unique to enzyme kinetics studies, we sought to develop a generalizable error propagation approach. As a result, we developed a computational approach for error propagation based on bootstrapping, which is independent of the mathematical model used to describe the data, and thus applicable beyond the Michaelis–Menten model.

We implemented our approach in three stages as illustrated for immobilized enzyme kinetics measurements in Figure 2. Equivalent analysis for in-solution control experiments is provided in Figure S3. First, we created a fluorescent product calibration curve (Figure 2A) and used bootstrapping to obtain distributions of calibration slope and intercept parameters (Figure 2B and C). The standard error in the calibration slope and intercept terms were ± 104 AFU/μM and ± 48.9 AFU, respectively. The bootstrap estimates of uncertainty in the calibration parameters were ≤ 10% higher than the standard errors calculated from the conventional method (Experimental Section). Next, we applied the bootstrap calibration parameter estimates to the raw kinetics data to generate calibration-corrected kinetics data sets. We bootstrapped from each calibration-corrected kinetics data set to generate a distribution of initial reaction rates for each of the original kinetics data sets (representative data in Figure 2D and E). In the last stage, we bootstrapped from the distributions of initial reaction rates and fitted the Michaelis–Menten model to each bootstrap sample, producing distributions of K_m and V_max (Figure 2F–H). We calculated the standard error in K_m and V_max estimates as the standard deviation of the corresponding distribution (Table 1).

Figure 2.

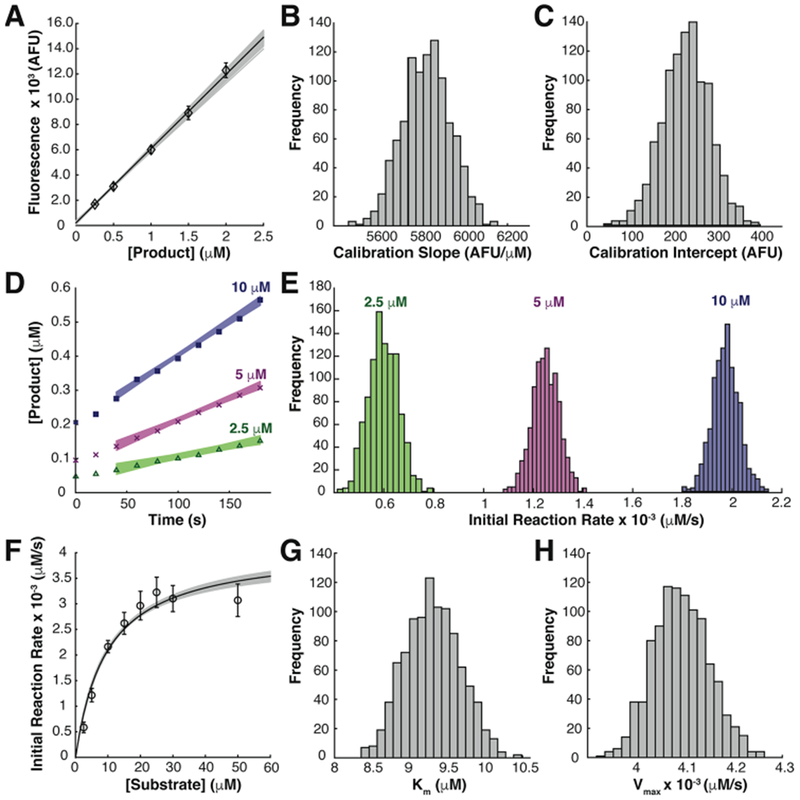
Bootstrapping method to propagate calibration error onto final uncertainty estimates of Michaelis–Menten model parameters. (A) Product calibration curve (black line) constructed from mean calibration slope and intercept of bootstrap samples overlaid with all possible calibration curves from bootstrap procedure (gray lines) and means of original calibration data (◊, n = 7 per concentration). (B, C) Distributions of product calibration parameters from bootstrap procedure. (D) Representative calibration-corrected kinetics data sets from gel regions exposed to (Δ) 2.5, (×) 5, and (■) 10 μM DiFMUP solutions overlaid with all possible linear fits from bootstrap calibration-corrected kinetics data sets yielded distributions of initial reaction rates (E) extracted from the slope term of the linear fits from all bootstrap calibration-corrected kinetics data sets. (F) Michaelis–Menten curve (black line) constructed from mean K_m and V_max parameters from all initial reaction rate bootstrap samples overlaid with all Michaelis–Menten curves from bootstrap procedure (gray lines) and mean initial reaction rates (O, n = 8 initial reaction rate measurements per concentration). (G, H) Distributions of Michaelis–Menten model parameters from bootstrap procedure. All error bars represent one standard deviation of the mean.

For comparison, we estimated uncertainty in K_m and V_max using the conventional method, which assumes negligible error in the product calibration data. The uncertainties in K_m and V_max calculated from the bootstrap method were ~4× lower than the standard errors calculated with the conventional method (Table 1). We hypothesized that neglecting the error in the product calibration data is acceptable in instances for which the conventional method yields more conservative estimates of the uncertainty in each parameter. To test this hypothesis, we simulated increased variability in the original product calibration data, generated new estimates of K_m and V_max, and compared the respective parameter uncertainties estimated from the conventional and bootstrap methods. To simulate increased variability in the original product calibration data, we adjusted the residuals from the mean for each concentration in the calibration by a constant factor, and adjusted each observed value by its equivalent adjusted residual. The procedure above did not affect the estimated calibration slope or intercept, resulting in approximately constant estimates of the uncertainty in K_m and V_max with the conventional method (Figure 3). However, the increased variability in the product calibration data resulted in increased root-mean-square error normalized by the mean of all observations in the calibration curve (NRMSE). We propagated the increased variability in the product calibration curve onto the final uncertainty estimates in K_m and V_max with the bootstrap method. The results indicated that the uncertainty in K_m and V_max obtained from our bootstrapping approach scaled proportionally with NRMSE, but at different rates (Figure 3). We conclude that error in the product calibration data is only negligible for NRMSE ≤ 0.05%, when the conventional method yields more conservative estimates of the uncertainty in both K_m and V_max. In the 0.05% ≤ NMRSE ≤ 0.06% regime, our bootstrap method provides a more conservative estimate of the uncertainty in K_m, while underestimating the uncertainty in V_max by ≤ 1% relative to the conventional method (Figure 3). As a result, we conclude that error in the product calibration data is non-negligible when NRMSE > 0.05%, and thus recommend the bootstrapping approach to propagate error in the product calibration data onto the final K_m and V_max estimates.

Figure 3.

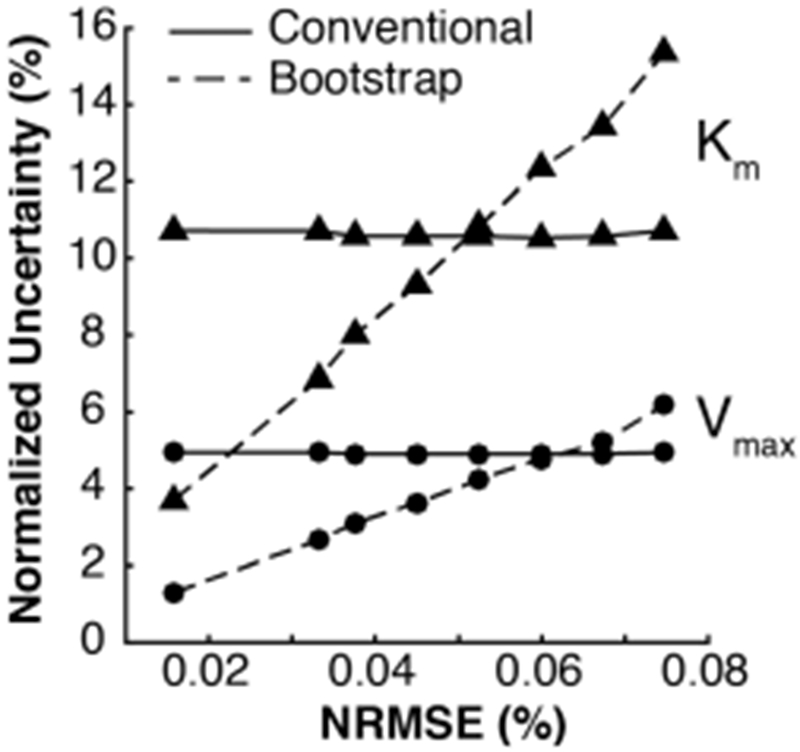
Uncertainty in Michaelis–Menten model parameters scales proportionally with the normalized root-mean-square error (NRMSE) of the product calibration data. Estimates of uncertainty in K_m (▲) and V_max (•) obtained from the conventional method (solid lines) are more conservative than uncertainty estimates produced from generalizable bootstrapping approach (dashed lines) for NRMSE ≤ 0.05%, suggesting the uncertainty in the product calibration is negligible in that regime.

CONCLUSIONS

We report on a measurement tool to characterize kinetics of enzymes immobilized in porous film arrays. To investigate the effect of immobilization of CIAP in BPMA-PAAm gels, we measured the concentration of CIAP immobilized in the gel, assessed the validity of Michaelis–Menten model assumptions in our system, and employed a quantitative framework to evaluate the presence of confounding mass transfer limitations. In the absence of mass transfer limitations, we observed ~2× and ~200× losses in the apparent enzyme substrate affinity (K_m) and intrinsic catalytic activity (k_cat) of immobilized CIAP, respectively, relative to in-solution measurements. We hypothesize that the changes in the apparent K_m and the intrinsic k_cat of immobilized CIAP arise from immobilization-induced changes in enzyme conformation and molecular mobility,²¹ as well as hindered access to catalytic sites.²⁰ These hypotheses are subject to further study with the density of the gel matrix, length of the immobilization linker, concentration of the immobilization monomer, and substrate molecular mass as possible experimental variables. The light-activated BPMA-PAAm immobilization mechanism offers precise spatial control over the distribution of immobilized enzyme in the gel, which may be attractive for some biosensor applications. However, the substantial decrease in intrinsic catalytic activity of CIAP upon immobilization in BPMA-PAAm gels suggests limited utility of this material to study native activity of enzymes from cells and/or for industrial applications. Furthermore, the effects of immobilization are expected to be enzyme–substrate pair specific, warranting investigation of the performance of BPMA-PAAm gels for immobilization of enzymes with important diagnostic, industrial, and analytical chemistry applications (e.g., glucose oxidase, heparinase, trypsin). Some enzymes may retain a higher fraction of the in-solution activity upon immobilization in BPMA-PAAm gels, which may require measurements at multiple enzyme concentrations to mitigate formation of substrate gradients. For laboratory-scale production of peptide fragments,⁷¹ our modular system would ease the purification of reaction products because the enzyme catalyst remains immobilized in the hydrogel. Moreover, the modular measurement tool presented can be utilized to study other porous immobilization supports so long as the material allows for fabrication of adherent films. We also present a computational approach to propagate calibration uncertainty onto final estimates of enzyme kinetics parameters, which can be readily modified to accommodate mathematical models beyond Michaelis–Menten kinetics. Taken together, our measurement system and error propagation methods offer generalizable tools with various applications in clinical diagnostics, bioprocessing, and analytical chemistry.