Figure 1: Principles for designing β-barrels.

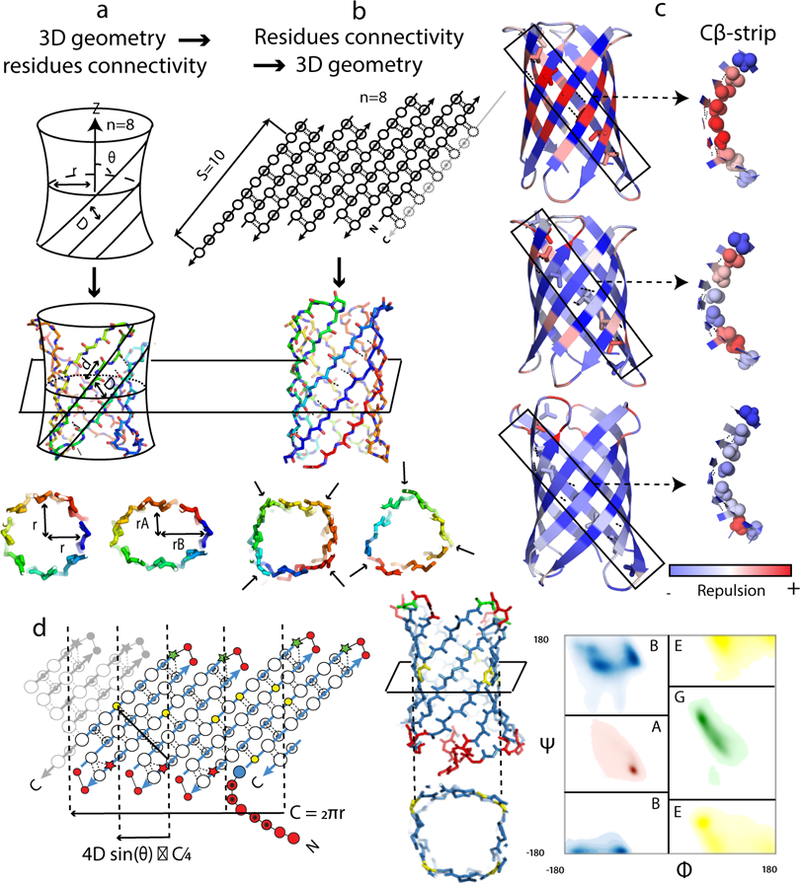
(a and b) Two methods for β-barrel backbone generation. a, Parametric generation of 3D backbones based on the hyperboloid model. The cross-section of the barrel is controlled on the global level with parameters (r, r_A and r_B). b, Specification of residue connectivity in a 2D map followed by assembly of 3D backbones with Rosetta. The cross-section geometry is controlled on the local level with torsion angle bins specified for each residue. c, Incorporation of glycine kinks and β-bulges reduces Lennard Jones repulsive interactions in β-barrels. Full backbones are shown on the left and one Cβ-strip is shown on the right. (Top) No β-bulge, no glycine kink; (Middle) one glycine kink in the middle of each Cβ-strip, no β-bulge; (Bottom) one glycine kink in the middle of each Cβ-strip, and β-bulges placed near the β-turns. d, Blueprint used to generate a β-barrel of type (n=8;S=10) with a square cross-section suitable for ligand binding. The values of the barrel radius (r) and tilt of the strands (θ) used to place glycines are determined by the choice of n and S. The residues in the 2D blueprint (left) and the 3D structure (middle) are colored by backbone torsion bins (right, Rosetta’s ABEGO types nomenclature). Shaded and open circles represent residues facing the barrel interior and exterior, respectively. Glycine positions are shown as yellow circles and β-bulges as stars. The “corners” in the β-sheet resulting from the presence of glycine kinks are shown as vertical dashed lines. C: barrel circumference; D: distance between strands.