Breast cancer risk from different mammography screening practises

Abstract

Mammography screening is an accepted procedure for early detection of breast tumors among asymptomatic women. Since this procedure involves the use of X rays, it is itself potentially carcinogenic. Although there is general consensus about the benefit of screening for older women, screening practices differ between countries. In this paper radiation risks for these different practices are estimated using a new approach. We model breast cancer induction by ionizing radiation in a cohort of patients exposed to frequent X-ray examinations. The biologically based, mechanistic model provides a better foundation for the extrapolation of risks to different mammography screening practices than empirical models do. The model predicts that the excess relative risk (ERR) doubles when screening starts at age 40 instead of 50 and that a continuation of screening at ages 75 and higher carries little extra risk. The number of induced fatal breast cancers is estimated to be considerably lower than derived from epidemiological studies and from internationally accepted radiation protection risks. The present findings, if used in a risk-benefit analysis for mammography screening, would be more favorable to screening than estimates currently recommended for radiation protection. This has implications for the screening ages that are currently being reconsidered in several countries.

INTRODUCTION

Breast cancer is the most prevalent cancer in women worldwide, with more than a million new cases occurring every year (1). The incidence is particularly high in Western populations. In some countries, such as the U.S. and the Netherlands, one in eight women are diagnosed with breast cancer during their life. Owing to improved treatment and earlier detection, the 5-year survival rate has increased over the last decades to 70–85%.

In Western countries, mammography screening is an accepted procedure for early detection of breast tumors among asymptomatic women. In the Netherlands, for example, women between 50 and 75 years of age are invited for a mammogram every 2 years, leading to approximately 900,000 screenings per year. Because the method employed involves the use of low-energy X rays to produce images of diagnostic quality, it is potentially carcinogenic. Although there is general consensus that screening is on balance beneficial for women between 50 and 70 years of age, risks and benefits of screening for both younger and older women remain controversial, and screening practices therefore differ from country to country. Furthermore, in several countries, such as the Netherlands and the UK, the ages at first screening are being reconsidered. This suggests the need for a radiation risk comparison between different practices. Back-of-the-envelope risk calculations with ICRP risk estimates (which are given in the Discussion section) indicate that screening could induce a fatal breast cancer in more than 200 women in the Netherlands over the period of screening and for a screening population of 900,000. More sophisticated estimates derived from epidemiological studies predict 30 to 50 fatal breast tumors per million women screened (2). However, ICRP risk estimates are based on linear extrapolations from high to low exposures, and epidemiological studies do not take into account the biological processes leading to breast cancer. This casts doubts on their validity at the low doses involved in mammography screening.

In this paper we try to improve the current risk estimates through the application of a biologically based, mechanistic model for breast cancer induction by ionizing radiation applied to a cohort of Western women exposed to frequent X-ray fluoroscopic chest examinations during lung collapse therapy for tuberculosis (TB). The two-mutation carcinogenesis (TMC) model that is used enables us to derive risk estimates for low-dose mammography exposures at the relevant ages (40–75 years).

METHODS

Data

The data used concern breast cancer incidence in a joint cohort of more than 6700 women treated for TB in Massachusetts (U.S.) between 1935 and 1954 (3, 4). At that time the treatment often included inducing pneumothorax or pneumoperitoneum (lung collapse) through the injection of air into the pleural or peritoneal cavity. To maintain a lung collapse for 3 to 5 years the amount of injected air was checked by fluoroscopy approximately every 2 weeks. Many patients therefore received over 100 fluoroscopies in total (5). The maximum annual breast dose was approximately 2 Gy, but doses per year for 70% of the exposed patients were between 0.1 and 0.4 Gy/year, with an average of 0.3 Gy/year. Total absorbed breast doses for exposed women were estimated to range from 4.4 mGy to 6.4 Gy. An average fluoroscopy lasted 15 s and delivered, on average, a dose of 15 mGy. Details about the fluoroscopy procedure and the calculation of breast doses can be found in Boice et al. (6). Apart from patients treated with lung collapse, the joint cohort also contains many TB patients who were treated differently, e.g. with bed rest or with surgery, and who were not exposed frequently to fluoroscopic X rays for lung collapse treatment. These patients serve as the control group. The relative risk calculated in ref. (3) for this cohort amounted to 1.61 at 1 Gy, and the authors reported an observed/expected breast cancer ratio of 1.29 for exposed women or approximately 33 excess cases on a total of 147 exposed cases (and 87 cases in TB patients treated differently).

Data were selected from the cohort in the following way: women who died before follow-up for cancer incidence was possible or for whom dose estimates were unknown were excluded, and 12 cases with more than one breast cancer were ignored because development of a second breast cancer is likely to be influenced by the therapy given for the first breast cancer. This led to a data set for modeling consisting of 4793 women, 2367 of whom were unexposed controls and 217 of whom were diagnosed with breast cancer. Apart from dose estimates, information on dose per year was available for 2279 of 2426 exposed patients (94%). The average (exposed) woman in this data set was born in 1916, was exposed from age 25–28 to 0.9 Gy, was followed up from age 43, and attained an age of 65 years at the end of follow-up.

Model

Following ref. (7), a two-mutation model is used to model breast cancer in the cohort (see Fig. 1). In this type of modeling it is assumed that a number (S) of sensitive cells can be transformed in a first mutational step (with stochastic rate μ₁) to intermediate cells (I) that have a growth advantage (ε) over normal sensitive cells. Intermediate cells can then be transformed in a second mutational step (with stochastic rate μ₂) to malignant cells (M). Once a cell has become malignant it is assumed to grow into a fatal tumor in a deterministic lag time (t_lag). Given S, the state of the system can be described by the numbers of intermediate and malignant cells I and M over time. The probability for certain values of I and M is governed by a Kolmogorov forward equation [see e.g. ref. (8)]. If P_i,m(t) denotes the probability that there are I intermediate and M malignant cells at time t and assuming ε(t) to represent the net growth advantage (i.e., without explicitly incorporating intermediate cell death) then the Kolmogorov equation has the following form:

$$d{\mathit{P}}_{i,m}(t)/dt=-\mathit{I}[\epsilon (t)+{\mathrm{\mu }}_2(t)]{\mathit{P}}_{i,m}(t)-\mathit{S}(t){\mathrm{\mu }}_1(t){\mathit{P}}_{i,m}(t)+(\mathit{I}-1)\epsilon (t){\mathit{P}}_{i-1,m}(t)+\mathit{S}(t){\mathrm{\mu }}_1(t){\mathit{P}}_{i-1,m}(t)+\mathit{I}{\mathrm{\mu }}_2(t){\mathit{P}}_{i,m-1}(t).$$

Figure 1.

Schematic representation of the two-mutation carcinogenesis model used in this study: sensitive, normal cells (S) can be transformed into intermediate cells (I) at mutation rate μ₁. The intermediate cells proliferate with a net growth advantage ε or become malignant (M) at mutation rate μ₂. The malignant cells grow into tumors in a lag time t_lag.

Summing the right-hand side over all possible values of I and setting M to 0, one can derive the following differential equation for P₀, the probability for no malignant cells at time t:

$$d{\mathit{P}}_0(t)/dt=-{\mathrm{\mu }}_2(t){\mathrm{\Sigma }}_{\mathit{I}}\mathit{I}{\mathit{P}}_{i,0}(t)=-{\mathrm{\mu }}_2(t)\mathit{E}(\mathit{I}|\mathit{M}=0){\mathit{P}}_0(t),$$

where E denotes the expectance. From this equation, P(t), the probability that M > 0 at time t (and hence the probability for cancer at time t+t_lag), is calculated as P(t) = 1 − P₀(t). The calculation of P(t) involves a numerical integration over time for which in this analysis a time step of 1 month is used. Note that the rate at which the first malignant cell develops, the hazard rate, is given by μ₂(t) E(I|M = 0). This hazard rate is used here to calculate (relative) risks.

The radiation action is assumed to take place in the two mutational steps (that may in reality represent several mutations), in the following way:

$${\mathrm{\mu }}_i={\mathrm{\mu }}_0(1+a_i\mathit{D}){\mathit{e}}^{-p_i(a_i\mathit{D})}(i=1,2),$$

where μ_i is the mutation rate for step i, μ₀ is the background mutation rate (also acting in the absence of ionizing radiation) for both mutational steps, D is the dose rate (dose per time step), and a_i and p_i are coefficients that are to be determined. If the number of sensitive cells is fixed, only the product of the background mutation rates in the two steps can be determined. For simplicity we assume them to be identical, but any set of values that leaves their product unchanged is equally likely. The exponential term represents cell killing when there is more cell damage than can be repaired. This occurs mainly at high dose rates. The standard model has seven free parameters: μ₀, a_i, p_i (i = 1,2), ε and t_lag. This set has been expanded with parameters taking up a birth-year effect. It has been shown (4) that a relationship exists between breast cancer incidence and birth year for several (Western) populations. Figure 1 of ref. (4) demonstrates a slightly more than linear increase in incidence rate from 1900 until 1950, a birthyear period that corresponds reasonably well with the birth years in the cohort under investigation (1876–1947, average 1916). Since this birth-year effect is probably an expression of changing lifestyles (e.g. diet, smoking habits, later first pregnancy, fewer children) over time, which are not included in our modeling, we need to correct for this. It has been shown (9) that the incidence rate is directly proportional to the product of the mutation rates in the model. Therefore, a birth-year scaling function for the mutation rates has been implemented of the form: μ_i´ = μ_i [1 + b (y − 1916)]^n/2 for i = 1,2, where b is a free parameter, y the actual birth year, and n a positive integer.

The preferred set of parameters is determined with a maximum likelihood method. The likelihood function that is evaluated is the product of the individual likelihoods for each woman. For a subject with a breast tumor at time of diagnosis t, the likelihood is given by the probability rate for a malignant cell dP/dt evaluated at the time of induction t − t_lag and corrected for the age at inclusion in the cohort. This probability rate can be calculated for any set of values for the model parameters. For a subject without a breast tumor at the end of follow-up t, the likelihood equals 1 − P(t − t_lag), again corrected for the age at inclusion. In practice, the total likelihood L, which is the product of all individual likelihoods, is a very small number and instead −ln(L) is minimized in a parameter search over all free parameters. Here we quote deviance values [the deviance being −2ln(L)] since deviances are assumed to be χ² distributed. Notice that through the use of individual likelihoods each individual is fitted at the same time (not grouped together) and depending on the state of the individual (case or non-case) either the probability for the presence of a tumor or the probability for the absence of a tumor is optimized. This means that many sets of parameters are drawn from the parameter space for which the likelihood is evaluated. A simulated annealing method is used to speed up this optimization process.

From a biological point of view this model may seem rather elementary, describing the complex process of carcinogenesis in terms of just a few rate-limiting steps. However, in practice it has proven to capture some essentials of carcinogenesis by accurately fitting to incidence and mortality data of numerous tumor types in animals and humans [see for example refs. (10–14)].

Apart from that, the model resembles the progression of a typical breast cancer as indicated in ref. (15) in that first atypical ductal hyperplasia (ADH) occurs, which is still benign, followed by a ductal carcinoma in situ (DCIS), which is malignant and which grows into invasive breast cancer (IBC). In addition, it has been shown (7) that the two-stage model can accurately describe the breast cancer incidence in diverse populations. This is achieved partly by the introduction of an age-dependent pool of sensitive cells. Many of the known risk factors for breast cancer, such as early menarche, low parity, late first pregnancy, late menopause, long-term use of oral contraceptives, and estrogen replacement therapy, are related to hormonal exposure. This hormonal exposure has an effect on cell proliferation [see e.g. ref. (16)]. If an increased proliferation concerns the sensitive or intermediate cells, risk for breast cancer will go up. Similar to ref. (7), we therefore assume that the hormonal influences can be modeled by variations in the number of sensitive cells with age.

Although the absolute number of sensitive cells is not crucial in our modeling (since only the product μ₀²S can be determined), the age dependence of this number is important. There is general consensus that the target cells for breast cancer are epithelial stem and progenitor cells (17, 18). Even though stroma is also radiation sensitive and may be involved in breast carcinogenesis, it is unlikely that it contains target cells. Different types of breast cancer such as invasive ductal carcinoma and invasive lobular carcinoma may result from the different types of epithelial cells and their locations in ducts and lobules (17, 19, 20). The percentage of epithelial tissue in the human breast was determined by Gertig et al. (16). For adult women under 30 they found 7.5% epithelial tissue. This may represent an overestimate because it was derived from biopsy material. However, because only the age dependence of the amount of epithelial tissue is really important, this is not a problem. Using an average volume of approximately 450 ml per breast as determined by Kovacs et al. (21), this leads to 34 ml of epithelial tissue. Assuming an average diameter of 5 µm per epithelial cell (22) and hence a spherical volume of 65 µm³, approximately 5 × 10¹¹ cells would fit in that amount of tissue. However, not all of these cells are stem or progenitor cells. It is estimated for rats that 3–8% of the mammary epithelial cells do not have a terminally differentiated phenotype (23, 24). Translated to humans this would amount to 1.5–4 × 10¹⁰ sensitive cells per breast or 3–8 × 10¹⁰ sensitive cells in total.

However, as stated earlier, the number of sensitive cells varies with age. It is likely that considerable numbers of stem and progenitor cells are already present before puberty. The histological sections shown in ref. (22) indicate that infants already have thousands of epithelial cells, a large fraction of which are probably still undifferentiated. Following ref. (7), we assume logistic growth during puberty, but instead of taking only 10 sensitive cells before puberty, we follow a different strategy: we assume that the number of sensitive cells in men and women is more or less the same before puberty. Furthermore, we assume that this number remains constant during the lifetime of an average male. Now the model can be used to calculate the spontaneous male breast cancer incidence (using only the radiation-independent parameters μ₀, ε and t_lag). Since the male incidence is known to be approximately 1% of the female incidence, the number of sensitive cells is estimated to be the number that results in a male incidence at age 70 that is 1% of the female incidence at that age (implicitly we assume that differences in hormones between men and women lead only to differences in numbers of sensitive cells). This leads to an estimate of 2.5 × 10⁸ sensitive cells. Note that these cells alone would only occupy a spherical volume with a 3-mm diameter. Hence for women the number of sensitive cells is assumed to grow from 2.5 × 10⁸ before puberty to approximately 5 × 10¹⁰ afterward, or an increase by a factor 200. Clearly these numbers come with a large uncertainty. However, it turns out that the model parameter values are fairly insensitive to the number of sensitive cells before puberty (over several orders of magnitude) and only μ₀ is influenced by the maximum number of sensitive cells after puberty. A change in the latter value leads to a simple scaling of this parameter.

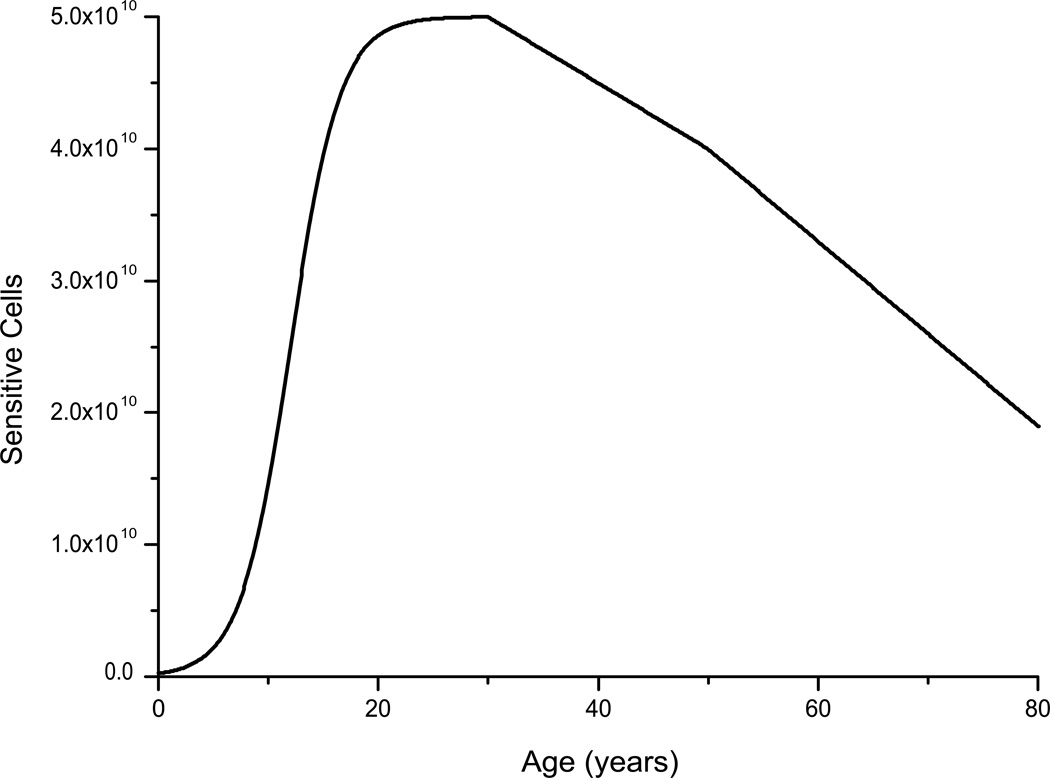
A second major influence on the number of undifferentiated epithelial cells is pregnancy and consecutive breast feeding. However, no information about the parity of the women in the cohort is available. Thus this effect could not be modeled. In general, the number of epithelial cells appears to decrease after age 30 (16). Surprisingly, this decrease seems to be accelerated only slightly by the advent of menopause. It is unknown whether the decrease in epithelial cells also takes place for undifferentiated progenitor cells, but we have assumed that the number of sensitive cells decreases linearly from age 30 onward and linearly and somewhat more steeply after the onset of menopause [based on the findings in ref. (16)]. The resulting age dependence of the number of sensitive cells is depicted in Fig. 2.

Figure 2.

Age dependence of the number of sensitive cells as implemented in the TMC model: before puberty 2.5 × 10⁸ sensitive cells are present that proliferate during puberty to 5 × 10¹⁰ cells. From age 30 this number decreases gradually according to data from ref. (16), and this decrease is accelerated at the onset of menopause. The ages of both puberty (12) and menopause (50) have been optimized in a series of model runs.

For all breast cancer cases, the age at diagnosis was used as the relevant time for modeling. In the model it is assumed that the first malignant cell that comes into existence grows into a tumor in a deterministic lag time. Hence it is implicitly assumed that all diagnosed breast cancers were of similar sizes that were attained in similar periods, i.e., with similar lag times. It is assumed in ref. (7) that a detectable breast tumor consists of approximately 10⁹ cells (if we assume the malignant cells to be of similar size as the epithelial cells, these would occupy a sphere 5 mm in diameter). To obtain this number of cells from a single malignant cell, 30 cell doublings are needed. A doubling time of 95 days has been derived from the growth of breast tumors (25). If this doubling time were constant up to the time of tumor detection, this would imply a lag time of 7.8 years. In ref. (7) the lag time is not fitted as a free parameter, but a fixed lag time of 5 years is assumed. This may be realistic if growth is faster in the initial stage of tumor development. However, individual tumor development before detection may be highly variable, and fits of the data indicate a preference for longer lag times of up to 15 years, depending on the age at puberty (see below). Since the breast cancers in the cohort were detected before the advent of screening mammography, it may be that they were detected relatively late. In ref. (26) tumor sizes for breast carcinoma have been summarized. Since most breast tumors in the cohort used here were detected after 1972 (155 out of 217), it seems appropriate to use a tumor diameter of 2 cm as given in ref. (26) for this period. For a tumor of that size, approximately 6 × 10¹⁰ cells are needed, or 36 cell doublings, implying a lag time of a little more than 9 years [using the 95-day doubling time in ref. (25)].

RESULTS

Preliminary model fits of the data were performed with seven free parameters (μ₀, a₁, a₂, p₁, p₂, ε, t_lag) and resulted in a deviance of 3023. Removal of a₂, p₁ and p₂ from the set of free parameters led to an increase in deviance of 0.25, indicating that these parameters are not statistically significant and that their values cannot be determined from the data. The removal of a₁ resulted in a jump in deviance of 19.60, indicating that a₁ is the only significant radiation-dependent parameter (P = 0.00001).

Next, several series of model fits were done to determine optimum values for the ages at puberty and menopause. These showed that the deviance is rather stable for menopausal ages between 45 and 55. The maximum difference in deviance is only 0.06. Therefore, an arbitrary choice for age 50 is used here. For the timing of the maximum growth of epithelial tissue during puberty, the minimum deviance is found at 8 years, which seems to be too young, but with a 95% confidence interval reaching up to age 13. Furthermore, this age is found to trade off with the lag time in the model fits. The fitted lag time decreases when the age of maximum growth increases from 7 to 15 and then reaches a more or less constant value of 9 years. Since 9 years seems to be a reasonable lag time and a non-optimum growth age seem unrealistic, a compromise for the age of maximum growth of 12 years is retained here.

Finally, the extra birth-year parameter b was fitted together with the other model parameters for n = 1,2. It turns out that the best fit is obtained for n = 2 [i.e. a linear scaling of the mutations rates and hence a quadratic effect on incidence rate (9)], although n = 1 leads to a very similar result. The deviance reduction amounts to 10.61, indicating that b is a very significant parameter (P = 0.001). The effect of the birth-year function on incidence rate in the model fit compares well with the findings in ref. (4) (not shown). The parameter values for this preferred fit to the cohort data are given in Table 1.

Table 1.

Parameter values and deviance for the preferred model fit.

Parameter	Value (95% CI)
μ0 [year−1]	2.50 (2.39 –2.61) × 10−8
a1 [year/Gy]	16.9 (9.72–24.4)
ε [year−1]	3.14 (2.61–3.63) × 10−2
tlag [year]	9.29 (7.10–12.0)
b [year−1]	1.43 (0.773–1.93) × 10−2
deviance	3012.85

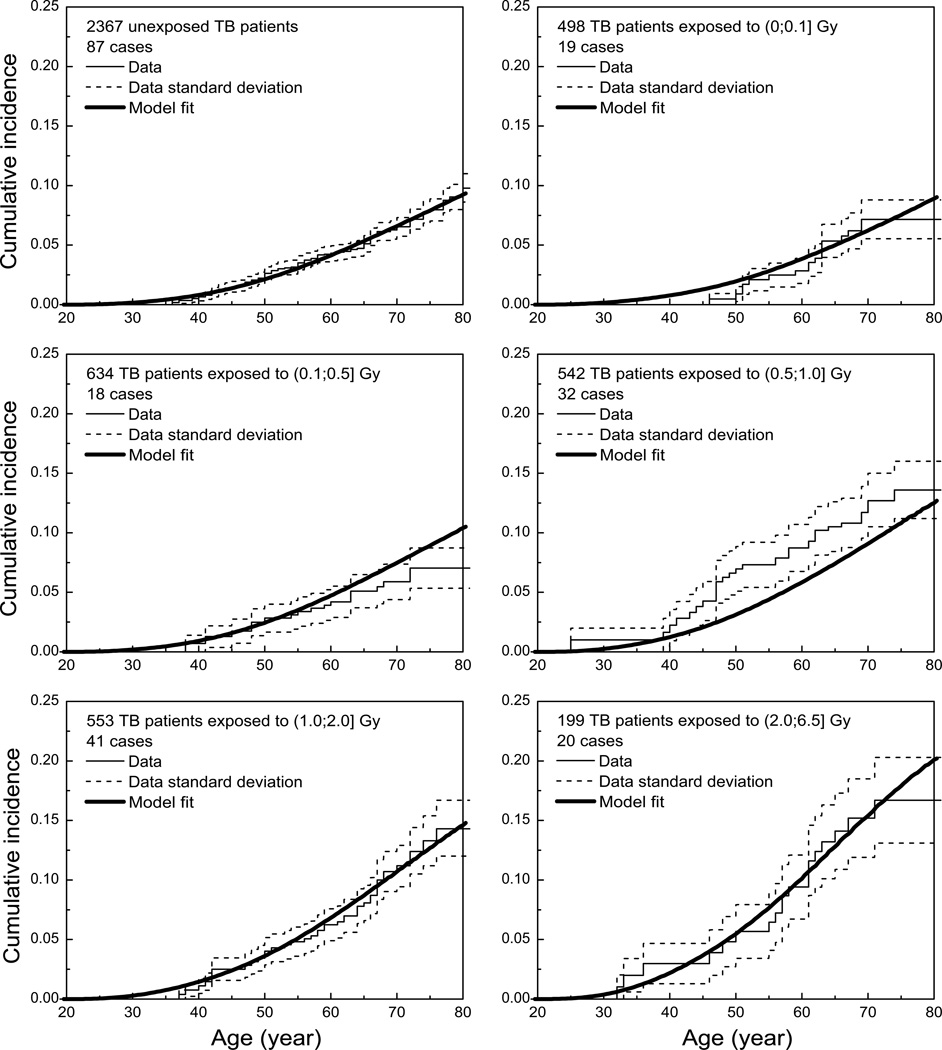
The parameter values in Table 1 have been used to calculate metrics that can be compared visually to the data. In Fig. 3 cumulative incidences for six groups of TB patients are shown. Note that the model depicted in this figure is not fitted directly to the Kaplan-Meier curves for the data but to all individual exposure and tumor data at the same time (as explained in the Methods section). Nevertheless, the model provides a good representation of the cumulative incidences derived from the data. Some deviation can be observed for the TB patient group exposed to 0.5–1.0 Gy, but the model curves for both the higher- and lower-dose groups are in close agreement with the data. This is especially important for low-dose extrapolations that need to be made for a comparison with mammography screening.

Figure 3.

Comparison of cumulative incidences calculated from the model and the TB patient data (Kaplan-Meier plots with errors calculated according to Greenwood's formula). The data have been grouped on the basis of total exposure.

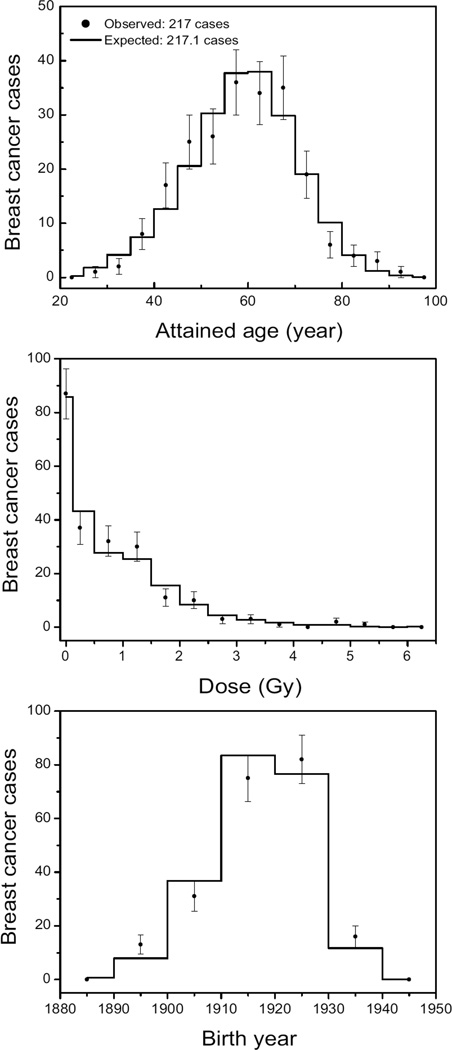
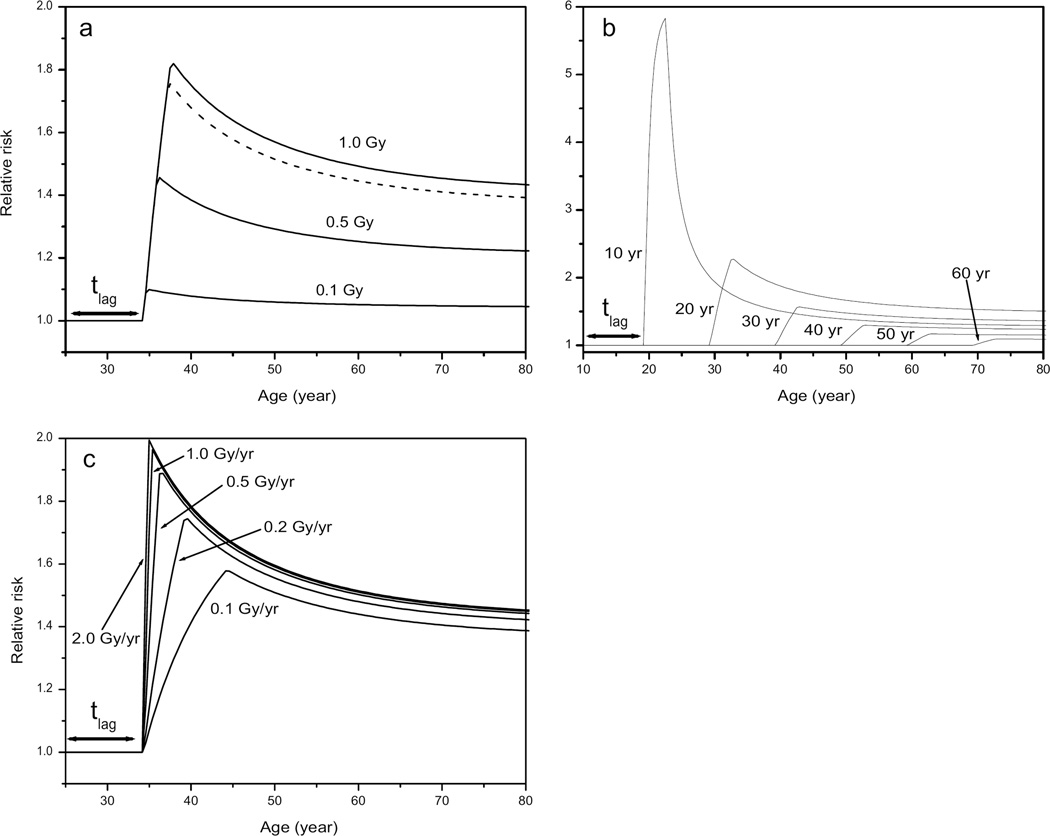
Another representation of the agreement between model and data is given in Fig. 4. This figure shows the observed number of breast cancer cases in the TB cohort as a function of age, cumulated dose and birth year and compares these to the expected number from a model calculation. It is clear from Figs. 3 and 4 that the fitted model parameters describe the data well. This provides confidence in the risk predictions that can be derived from the model. One measure of the risk is the number of excess cases due to the exposure. This can be derived from the number of expected cases calculated without any exposure (176.7) and the number of cases in the cohort (217). Hence the number of excess cases is approximately 40 (95% CI: 23–58). The preferred model parameters (see Table 1) can be used to calculate risks for different exposure scenarios. An example is given in Fig. 5, which shows relative risks against age for different total doses, different ages at exposure and different dose rates. It can be concluded that relative risks are highest for exposures at young ages. Note in particular that the relative risk after exposure at age 10 is much higher than those at ages 20 or 30 even though the number of sensitive cells at age 10 is only 20% of the maximum. Apart from the age response, risks increase steeply with total dose but less with dose rate. The relative risk for a TB patient exposed from age 25 to 28 to 1 Gy is 1.47 at age 65 (the average attained age in the cohort). Figure 5b can be compared with Table 7 and the left panel of Fig. 3 of ref. (4) for the TBO and TBX cohorts: both figures show (excess) relative risk as a function of age at exposure. The relative risks decrease in Fig. 5b from 1.53 to 1.25 for ages at exposure from 20 to 40 (and attained ages above 55). This is in reasonable agreement with the results for the TBO cohort in ref. (4) where these risks decrease from 1.39 to 1.04 for ages at exposure from 25 to 45. For the TBX cohort the relative risks remains nearly constant at 1.3.

Figure 4.

Number of breast cancer cases as a function of age, dose and birth year as derived from the TB cohort data (observed) and from model calculations (expected). Note that the number of women in each age, dose and birth year interval can be different. For this reason the number of cases decreases with dose, whereas the incidence increases with dose.

Figure 5.

Relative risk as a function of age for (panel a) women exposed from age 25 to 0.3 Gy/year for several cumulated doses (dashed curve is for 0.9 Gy, representing the average exposed woman in the cohort), (panel b) women exposed at ages from 10 to 60 years to 1.0 Gy at 0.3 Gy/year, and (panel c) women exposed from age 25 to dose rates from 0.1 to 2.0 Gy/year for a cumulated dose of 1.0 Gy.

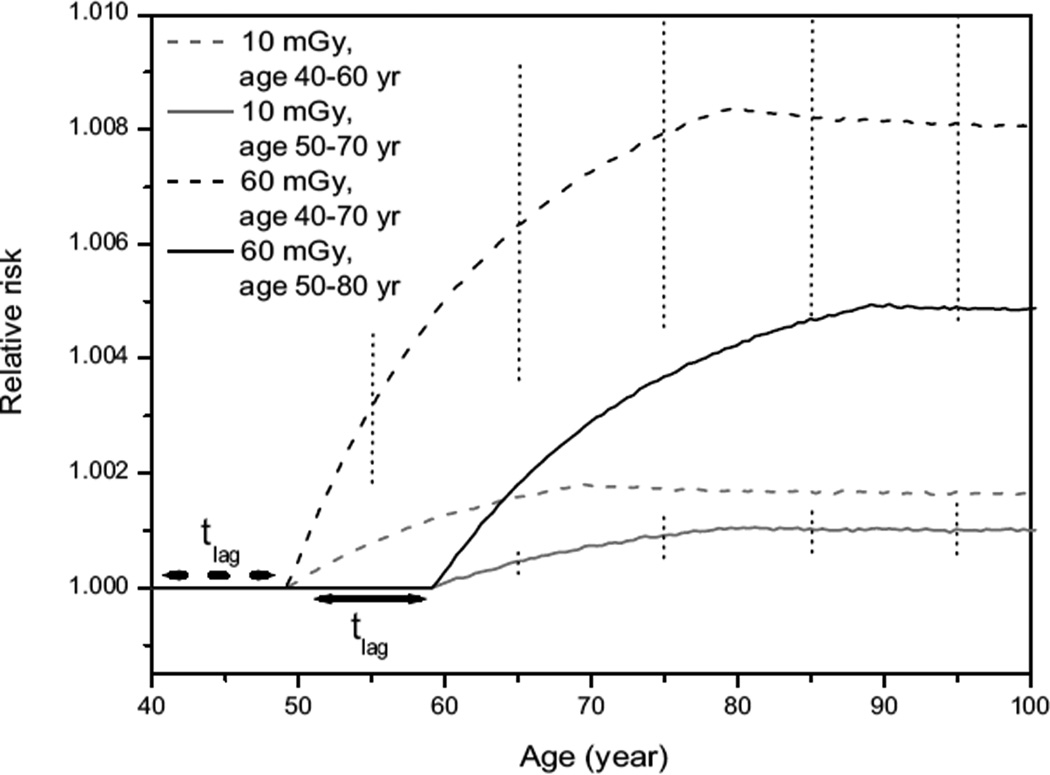
A very specific exposure scenario is that used in mammography screening. Although screening practices differ between countries and states, the average screening program would deliver doses of approximately 2–4 mGy per screening for a total of 5–15 screenings, leading to a cumulated dose of 10–60 mGy. Screening is usually performed during a 20–30-year period starting at an age of 40 or 50 years. The relative risks resulting from such doses averaged over such periods are depicted in Fig. 6. This figure also provides an indication of the 95% CI of the relative risks. Figure 6 shows that risks increase steeply after the first screening plus the lag time but tend to flatten for more advanced ages, indicating that a continuation of screening after age 75 will add less to the risk than screening before age 75. After screening has ended relative risks remain nearly constant. In addition, the excess relative risk (ERR) is almost doubled when screening starts at age 40 instead of 50 (for equal dose). The size of the 95% CI does not affect this conclusion: the CI is determined mainly by the uncertainty in the radiation-dependent parameter a₁, and any change in that parameter affects both ERRs in the same way, leaving their ratio unchanged. Similarly, the ERR after 60 mGy is approximately five times that of the ERR after 10 mGy (for equal starting age). In fact, it turns out that the ERR increases linearly with dose when considering equal screening periods at identical ages (not shown), because only the first mutation depends (linearly) on dose.

Figure 6.

Relative risks for different mammography screening practices. Gray lines are for 10 mGy (representing five screenings of 2 mGy), whereas black lines are for 60 mGy (representing 15 screenings of 4 mGy). Dashed lines are for screening starting at age 40 and solid lines are for screening starting at age 50. Dotted vertical lines indicate the 95% CI for the scenarios with the lowest and the highest cumulative doses.

The still relatively small ERR for earlier screening indicates that from a radiation protection perspective there is little objection to screening at younger ages. This is an important finding regarding the current tendency for earlier screenings: in the UK the starting age has recently been lowered to 47 years, and in the Netherlands a starting age of 45 years is currently being considered.

From these results the number of breast cancers induced by these screenings can be calculated. For five 2-mGy screenings starting at 40 or 50 years, these calculations predict that 14.6 and 12.7 cancers would be induced per million screened women, respectively. For 15 4-mGy screenings from ages 40 and 50, these numbers are 235 and 200 per million screened women, respectively. Note that since breast cancer incidence data have been used in these calculations, the number of cancers is estimated, not the number of fatalities.

DISCUSSION

Comparison with Epidemiology

Extensive epidemiological research has been conducted on radiation-induced breast cancer. The cohort data used in this study for mechanistic modeling have also been used in several epidemiological studies, such as ref. (3). It is therefore interesting to compare the results: in ref. (3) 33 excess breast cancers are estimated for nearly the same data. This compares well with the estimate in this study of 40 excess cases. Similarly, the relative risk at 1 Gy calculated in ref. (3) of 1.61 (95% CI: 1.30–2.01) is in good agreement with the estimate in this study of 1.47 (for an average exposure profile and at age 65).

Recently, pooled epidemiological studies for radiation-induced breast cancer have been performed by Boice (5), who compared 14 cohorts, and Preston et al. (4), who analyzed eight cohorts. In general a linear dose response is found and a decrease of risk with increasing age at exposure. This decrease is also clearly present in the preferred model fit of this study for ages of 20 and above (see Fig. 6b) and a linear dose response follows from the fact that a (linear) dose dependence is found only for the first mutation rate in the model. In ref. (4) ERRs/Gy of 0.29 (−0.06–0.8) and 0.39 (<0–1.02) are found for the two cohorts that are combined here. These numbers agree very well with the relative risk of 1.47 per Gy (i.e. ERR/Gy of 0.47) calculated here. Their pooled analysis yields an ERR/Gy of 0.74 (0.4–1.2), which is still in agreement with the results of this study within the limits of the confidence interval.

Estimates of Casualties Induced by Mammography Screening

An important advantage of mechanistic modeling over epidemiological modeling is that the incorporation of a biological mechanism allows for a more sophisticated extrapolation of the results to exposure scenarios that are not incorporated in the data. Even though the TB patients in the cohort under investigation were on average first exposed at age 25 and very few were first exposed at ages above 50, the mechanistic model enables risk calculations for much higher ages at exposure under the assumption that the carcinogenic mechanism in the model is still valid. In this way risks for mammography screening exposures have been calculated (see Fig. 6). These risks can be compared to other estimates. ICRP Publication 103 gives estimates of detriment-adjusted nominal risk coefficients for all cancers for adults (male and female) together: 4.1% per Sv (27). The ICRP estimate is based on data on cancer incidence, is weighted for lethality and life impairment, and is meant for radiation protection purposes. The collective effective dose of all mammography screenings in the Netherlands is approximately 389 Sv per year: 900,000 screenings × 1.8 mGy × the tissue weighting factor of 0.12 × 2 (because the tissue weighting factor represents an average for men and women and here only women are involved). In the Netherlands, women are screened every 2 years from age 50 to 75, so the total collective effective dose amounts to 5057 Sv. Even though ICRP detriment-adjusted nominal risk coefficients are not meant for risk estimation, one could estimate that this would lead to 207 fatal breast tumors among the 900,000 women screened. Similarly, in the United Kingdom the collective glandular dose from mammography screening has recently been estimated at 8094 Gy per year (28). This amounts to 971 Sv per year using the new ICRP 103 tissue weighting factor. In the United Kingdom women are screened every 3 years from age 50 to 70 so the total collective effective dose is 6797 Sv. Again using ICRP risks this would result in approximately 279 fatal breast tumors among the 1.7 million women screened.

Evidently, the risks for women aged 50–75 will be lower than the risk for an average adult. In ICRP 60 (29) an indication of this effect is given in Table B-9, quoting risk estimates as a function of age from the BEIR V report (30). From this table it is difficult to estimate the number of fatal breast cancers for a realistic screening program, but it is likely to be well below 40% of the number estimated using a risk of 4.1% per Sv, or for the Dutch case well below 83 cases. For the Dutch mammography screening, a detailed calculation of the excess mortality using the epidemiological models of refs. (4) and (30) has been made (2), taking into account the ages at exposure (50–75). Using a relatively low average dose per screening per breast of 1.3 mGy, their estimates range from three to five excess fatal breast cancers per 100,000 screened women or 27–45 cases for the screened population (900,000) after these women complete the entire screening program. Assuming that the model presented here based on women from Massachusetts can be applied to Dutch women and using 13 screenings of 1.8 mGy per breast from age 50 to 75, it predicts 45 cases for 900,000 women after the entire screening program. Despite the higher doses used in the calculation, this is considerably lower than the epidemiologically based estimate of ref. (2), depending on the survival rate. A survival rate of 70% would yield only 14 fatal breast cancers, a survival rate of 85% only seven fatal cases. The approximately 10 fatalities predicted by our model to be induced by the Dutch screening program should be compared to the number of lives saved. The latter is difficult to estimate, because the observed reduction in mortality due to breast cancer in the Netherlands since the introduction of screening (some 25% or approximately 1000 lives per year) cannot be attributed fully to screening alone. Clearly improved treatment, increased breast cancer awareness and a diminished use of hormone replacement therapy also contribute to this reduction. It is estimated (31) that the English and Welsh screenings have contributed to the observed reduction by approximately one-third. For the Dutch case this would imply that screening alone saves more than 300 lives every year. This clearly outweighs the number of fatalities induced.

Influence of Hormones and Genetic Factors

As stated before, there is little information about hormone levels in the individual members of the cohort studied. This prevents the application of models such as developed in refs. (32, 33). There is only limited individual information on hormonal influences such as parity, ages at menarche and menopause, and so on (34). It is well known that these factors have a profound impact on breast cancer risk. We have therefore implicitly assumed that differences in these factors between individuals are smoothed out by the statistics of the large data set, and this may indeed be inferred from the quality of the model fit achieved. Apart from that, the general influence of hormones has been modeled indirectly as affecting the proliferation of sensitive cells. Again, from the excellent model fit it may be concluded that this is a valid approach. Finally, it is well known that genetic factors can play a role in breast cancer induction. A risk factor that is often mentioned is a family history of breast cancer. It should be noted that this factor includes not only shared genetic factors but also shared environmental factors. The purely genetic factor mainly involves the BRCA1 and BRCA2 genes and to a lesser extent the ATM and p53 genes. For the cohort data under consideration these factors are generally unknown. However, the BRCA1 and BRCA2 genes are implicated in less than 10% of all breast cancer cases (35, 36). Furthermore, the role of ATM is a subject of ongoing debate (35, 37). With respect to genetic and environmental factors it is also interesting to note that although Asian populations generally carry a lower risk for breast cancer, the breast cancer incidence in U.S. women of Asian descent has become similar to the general incidence in U.S. women in a few generations' time (38). This indicates that not only genetic but environmental factors (such as exposure to phytoestrogens from soy) play a major role here. Hence the vast majority of breast cancer cases cannot be attributed to known genetic factors at this time.

Conclusions

In this study a new approach has been attempted to calculate radiation risks for mammography screening practices. A mechanistic model for carcinogenesis that is relatively simple from a biological perspective has been applied to a cohort of frequently exposed TB patients. It turns out that this simple model, in which hormonal influences are affecting only general proliferation rates of target cells, describes the data rather well. In addition, the results are in good agreement with epidemiological studies. More importantly, the biologically based modeling allows for a better foundation for extrapolation of risks to other exposure patterns, such as those of different mammography screening practices. For mammography, it is predicted that the ERR doubles when screening starts at age 40 instead of 50 and that a continuation of screening at ages of 75 and higher carries relatively little extra risk. ERR increases linearly with the cumulated dose of screening but remains below approximately 1% for current screening practices in Europe and the U.S. This indicates that lowering screening age from 50 to 45 is not contraindicated from a radiation protection perspective. The number of fatal breast cancers induced by screening is estimated to be approximately 10 for the entire Dutch screening. This is considerably lower than a previous epidemiological estimate of 27–45 fatalities in this population and much lower than derived from the inappropriate but often used ICRP 103 risk estimates (27). The present findings, if used in a risk-benefit analysis for mammography screening of asymptomatic women, would be more favorable to screening than the estimates recommended for radiation protection.