Fig. 1.

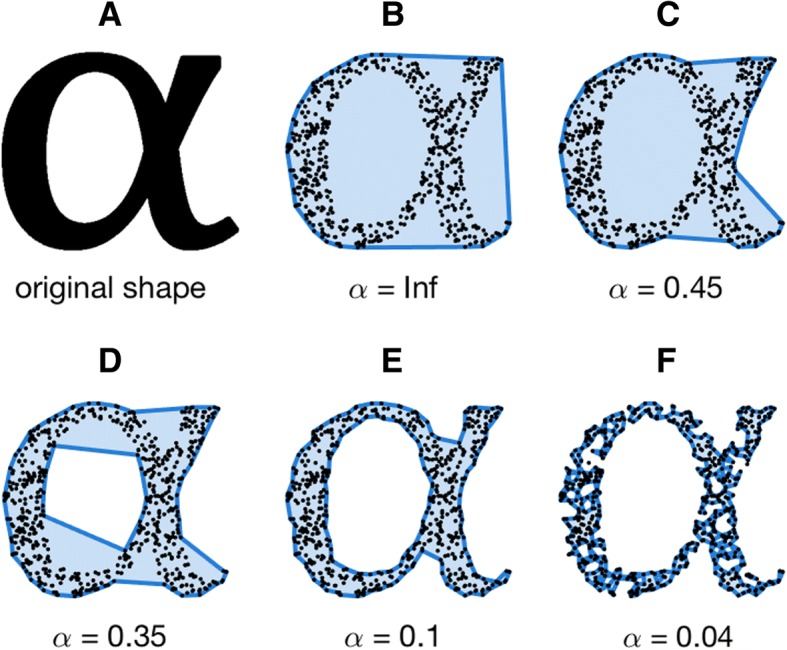
Diagram illustrating the nature of alpha-shapes, as understood in 2-dimensions. a, the original shape to which alpha-shapes are to be fitted; b, a convex hull fitted to the data representing the special case when alpha = infinity; c-e, represent increasingly refined alpha-shapes fitted to the data as alpha is reduced; f, represents the point at which the alpha radii can pass ‘internally’ through the data set and the alpha-shape breaks down to form several smaller shapes. Intuitively, the alpha-shape represented in Fig. 1e would be considered as ‘most-representative’ of the original shape described in Fig. 1a, as defined by equivalency of area