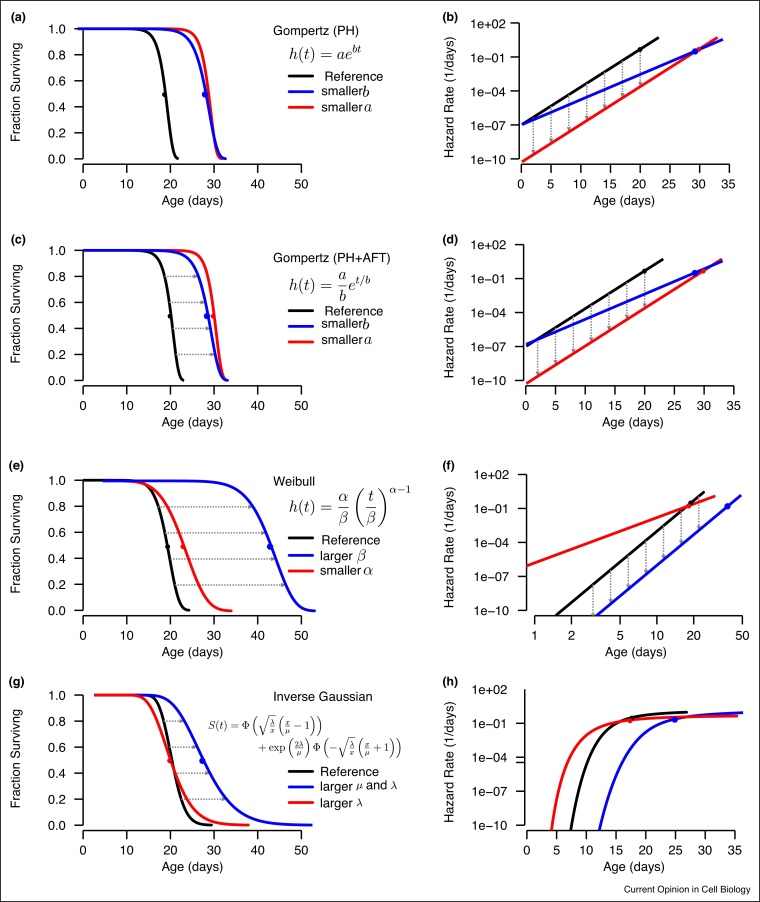
Figure 2.

Parametric models of lifespan data. Various simple functions have been proposed to approximate empiric lifespan data, shown as models of survival functions (left) and (right) hazard functions. Median lifespan is marked as a single point on each corresponding curve. Geometric regularities in the influence of various parameters are marked with gray arrows. (a,b) The Gompertz distribution is commonly employed with the parameter a that determines the risk of death in animals of zero age and b that determines the rate of increase in risk over time. (c,d) The alternate parameterization of the Gompertz model removes the implicit and often missed time-scale dependence of the a parameter, allowing changes in initial mortality and changes in doubling time to be isolated, and allowing the Gompertz function to model both changes in proportional hazards and changes in timescale. (e,f) The Weibull distribution models hazard functions that increase as a polynomial of time (in contrast to the exponential increase assumed in by the Gompertz model). Weibull hazard functions therefore form straight lines when plotted on log–log axes, rather than log-linear axes. (g,h) Inverse Gaussian distributions exhibit inherently decelerating hazard functions, and provide a link between lifespan data to the theory of Weiner Processes and Brownian motion.