Figure 7. External constraints on apical-basal (AB) polarity and planar cell polarity (PCP) can initiate invagination and drive gastrulation in sea urchin.

(A) The lower third of the cells in a blastula with AB polarity (apical is blue–white, basal is red–orange) pointing radially out acquire PCP (cyan–green) in apical plane pointing around the anterior-posterior (top-bottom) axis (as in the inset to Figure 6). (B) Flattening of the blastula and (C) invagination occur due to external force reorienting AB polarity (Materials and methods). (D–E) Tube elongation is due to PCP-driven convergent extension and (F) merging with the top of the blastula happens when the tube approaches the top. Throughout the simulation, λ₁ = 0.5, λ₂ = 0.4, and λ₃ = 0.1 for the lower cells while the top cells have λ₁ = 1 and λ₂ = λ₃ = 0. For full time dynamics see Figure 7—video 1. In Figure 7—figure supplement 1, we consider alternative scenarios of sea urchin gastrulation and and neurulation.

Figure 7—figure supplement 1. Directed changes in the direction of planar cell polarity (PCP) may drive invagination in gastrulation and neurulation.

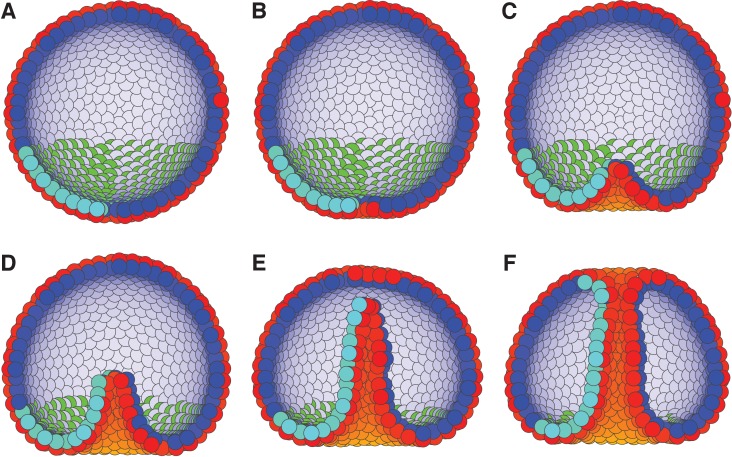
(A–D) Gastrulation in sea urchin modeled without the apical constriction in Figure 7. (A) The lower third of the cells in the blastula acquire PCP (cyan–green) pointing opposite to the apical-basal (AB) polarity (red–yellow). (B) Flattening of the blastula and invagination occur if direction of PCP is maintained for some time. During this initial phase λ₂ = 0.1, and there is no convergent extension (λ₃ = 0). (C) In the final phase, we increase λ₂ to 0.4 and turn on λ₃ = 0.1. With this, we let PCP relax so it curls around the bottom, and allow it to change dynamically in time. (D) As a result, tube narrows and elongates, until it finally connects and merges with the top. 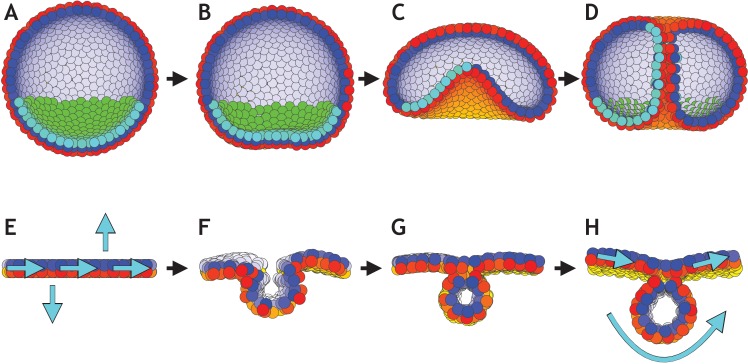(E–H) Initial conditions on PCP enable neural plate bending and neural tube closure. (E) Starting with 1000 cells on a plane with AB polarity, we induce PCP along the plane together with two rows where the PCP points parallel and antiparallel to AB polarity (shown with cyan arrows). Here, we simulate the neural plate (cells in the middle, between the two rows with constrained PCP) surrounded by the epidermis (the rest of the cells). The two rows of cells with PCP pointing out of epithelial plane correspond to the cells at the dorsolateral hinge points next to the neural plate (epidermis boundaries). In chick, spinal neural tube can close with only these two hinge points (Nikolopoulou et al., 2017). The bending is driven by apical constriction and PCP is essential for bending, convergent extension and closure. (F) This enables neural plate bending and formation of the neural groove. (G) Continuing the simulation leads to contact of the two sides of the neural plate and hereby neural tube closure. (H) Finally, the system stabilizes with the neural plate on top of the neural tube. Comparing the initial stage to the final stage, the overall direction of PCP in the plate is conserved while in the tube PCP goes around an internal axis. For this simulation, we set λ₂ = 0.5 and λ₃ = 0. Turning on convergent extension (λ₃) at the final stage will allow for elongating the system along the axis going through the tube and narrowing it in another direction. The concept is similar to gastrulation in Drosophila. In both simulations, sea urchin and neurulation, dt = 0.3. In sea urchin (A–D), the noise parameter η = 3.3⋅10⁻⁵, and in neurulation (E–H), η = 3.3⋅10⁻².

Figure 7—video 1. Model of sea urchin gastrulation.

Download video file ^{(10.1MB, mp4)}

DOI: 10.7554/eLife.38407.026

Starting from a hollow sphere of 1000 cells with apical-basal polarity pointing radially out. The bottom flattens and invaginates by applying an external force to mimic apical constriction (see Materials and methods), and by giving a fraction of cells planar cell polarity pointing around the sphere. The tube forms, elongates, and connects with the upper part of the blastula. Throughout the simulation, dt = 0.1 and η = 10⁻⁴. For more details see the caption to Figure 7. Panels are similar to Figure 6—video 1. The color scheme is as described in Figure 3 and Figure 7.