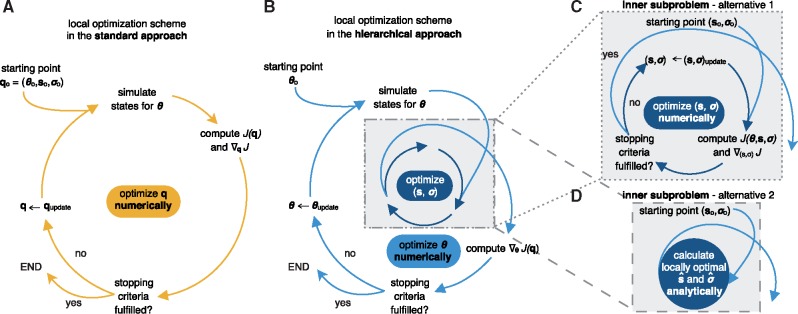
Fig. 1.

Visualization of standard and hierarchical optimization schemes. (A) Local optimization in the standard approach with parameters $\mathbf{q}=(\mathit{\theta },\mathbf{s},\mathit{\sigma })$. A single iteration includes the numerical simulation of the ODE model for $\mathit{\theta }$, the evaluation of the objective function and its gradient, the evaluation of stopping criteria, e.g. local optimality, and the termination of the local optimization or the updating of the parameters. (B) Outer local optimization in the hierarchical approach with parameters $\mathit{\theta }$. A single iteration includes the numerical simulation of the ODE model for $\mathit{\theta }$. the evaluation of the objective function and its gradient with respect to $\mathit{\theta }$ using the results of the inner optimization problem. The iteration also includes the evaluation of stopping criteria, and the termination of the local optimization or the updating of parameters. (C, D) Inner (local) optimization in the hierarchical approach to find the optimal scaling and noise parameter $\widehat{\mathbf{s}}$ and $\widehat{\mathbf{\sigma }}$ for given dynamic parameters $\mathit{\theta }$. (C) Iterative local optimization to determine $\widehat{\mathbf{s}}$ and $\widehat{\mathbf{\sigma }}$. This does not require the numerical simulation of the model. (D) Calculating optimal parameters $\widehat{\mathbf{s}}$ and $\widehat{\mathbf{\sigma }}$ using analytic expressions for common noise distributions