Compressed Sensing Acceleration of Biexponential 3D-T_1ρ Relaxation Mapping of Knee Cartilage

Abstract

Purpose

Use Compressed Sensing (CS) for three dimensional (3D) biexponential spin-lattice relaxation time in the rotating frame (T_1ρ) mapping of knee cartilage, reducing the total scan time and maintaining the quality of estimated biexponential T_1ρ parameters (short and long relaxation times and corresponding fractions) comparable to fully-sampled scans.

Methods

Fully-sampled 3D-T_1ρ-weighted datasets were retrospectively undersampled by factors 2–10. CS reconstruction using twelve different sparsifying transforms were compared for biexponential T_1ρ-mapping of knee cartilage, including temporal and spatial wavelets and finite differences, dictionary from Principal Component Analysis (PCA), K-means Singular Value Decomposition (K-SVD), and exponential decay models, and also low rank and low rank plus sparse models. Synthetic phantom (n=6) and in vivo human knee cartilage datasets (n=7) were included in the experiments. Spatial filtering prior to biexponential T_1ρ parameter estimation was also tested.

Results

Most CS methods performed satisfactorily for an acceleration factor (AF) of 2, with relative median normalized absolute deviation (MNAD) around 10%. Some sparsifying transforms, such as low rank with spatial finite difference (L+S SFD), spatiotemporal finite difference (STFD), and exponential dictionaries (EXP) significantly improved this performance, reaching MNAD below 15% with AF up to 10, when spatial filtering was used.

Conclusion

Accelerating biexponential 3D-T_1ρ mapping of knee cartilage with CS is feasible. The best results were obtained by STFD, EXP and L+S SFD regularizers combined with spatial pre-filtering. These three CS methods performed satisfactorily on synthetic phantom as well as in vivo knee cartilage for AFs up to 10, with median error below 15%.

INTRODUCTION

Osteoarthritis (OA) is the most common form of arthritis and a leading cause of chronic disability in the elderly population (1,2). Currently, OA affects more than 27 million people in the United States alone, generating high expenses to the healthcare system (3,4). OA is connected with the degradation of components of the extracellular matrix (ECM) of articular cartilage (5), mainly composed by proteoglycan (PG), collagen fibers and water (6). Early diagnosis of cartilage degeneration requires detection of changes in PG concentration and collagen integrity, preferably noninvasively and before morphological changes occur (7,8).

The spin–lattice relaxation rate in the rotating frame (R_1ρ) has been shown to decrease linearly with the decreasing PG content of articular cartilage (9). Several researchers (10,11) have demonstrated that the spin–lattice relaxation time in the rotating frame (T_1ρ) is more sensitive to proteoglycan content of the cartilage, while spin–spin relaxation time (T₂) is more sensitive to collagen orientation and integrity of network and hydration. Most of the previous studies (7,8,11) have utilized the monoexponential models to characterize the T_1ρ relaxation mapping of articular cartilage in the knee joint. However, the monoexponential estimation of T_1ρ alone is not able to provide information on short and long components and their fractions.

Recent studies (12–14) have shown that T_1ρ relaxation may have multiexponential components, following the hypothesis of multicompartmental structure. In (13), it was shown that biexponential models for T_1ρ can bring more information about the ECM composition in human knee cartilage.

The quantitative 3D-T_1ρ mapping usually requires the use of four or five T_1ρ-weighted images with different spin-lock lengths (TSLs) to obtain the monoexponential T_1ρ maps (15). However, biexponential analysis of cartilage typically requires a larger number of TSLs in order to maintain accuracy and the precision of biexponential T_1ρ quantification (13), resulting in a long scan time. High spatial resolution is also needed in order to visualize the thin and curved cartilage and fine structures in the knee joint. As a result, in vivo application of biexponential 3D-T_1ρ mapping techniques is still very limited.

An effective alternative is compressed sensing (CS) (16) to reduce the total scan time in quantitative T_1ρ mapping. This fast magnetic resonance imaging (MRI) uses pseudo-random k-space undersampling (17) that generates (intentionally) noise-like artifacts in standard reconstruction. However, exploiting the compressibility, or sparsity, of magnetic resonance (MR) image representation in transformed domains, CS effectively removes these artifacts, recovering most of the original image (18). Moreover, CS can make use of multicoil, or parallel, imaging for further increases in speed (19). Recently, several CS methods have been applied to high-dimensional MR imaging such as dynamic imaging (20,21). Moreover, parametric relaxation mapping (22–25) is particularly suitable for CS due to increased compressibility in the parameter direction, which turns into higher accelerations.

Studies such as (25–29) and (30) have demonstrated that a reduction in acquisition time using CS is possible for monoexponential T_1ρ mapping of cartilage, brain and intervertebral disc. Nevertheless, the feasibility of CS for biexponential T_1ρ mapping has not been demonstrated yet.

In this paper, we extend our previous experiments of CS for monoexponential mapping (30) to biexponential mapping. The feasibility of using CS to accelerate biexponential 3D-T_1ρ mapping is evaluated for knee cartilage by comparing twelve different types of sparsity promoting functions on synthetic phantoms (with and without noise) and in vivo knee cartilage datasets. Our main aim is to answer the question of what are the best regularization penalties and suitable acceleration factors for CS reconstruction with least components error when the final objective is to reduce image acquisition time of biexponential 3D-T_1ρ mapping of human articular cartilage.

METHODS

MRI Data Acquisition and Standard Reconstruction

Seven in vivo human knee 3D-T_1ρ-weighted datasets were acquired with 10 different TSLs using a modified 3D Cartesian turbo-Flash sequence (13). The MRI scans were performed using a 3T clinical MRI scanner (Prisma, Siemens Healthcare, Erlangen, Germany) with a 15-channel Tx/Rx knee coil (QED, Cleveland OH). The 3D-T_1ρ acquisition parameters were: TR/TE=7.5ms/4ms, flip angle=8°, matrix size 256×128×64, longitudinal magnetization restoration delay=1020ms, 64 k-space lines captured per preparation pulse, spin-lock frequency=500Hz, slice thickness=2mm, field of view (FOV)=120mm×120mm, and receiver bandwidth=515 Hz/pixel.

The T_1ρ-weighted scans of the knee were acquired in sagittal plane from seven healthy volunteers (age=29.6±7.5 years), with 10 TSLs including 2/4/6/8/10/15/25/35/45/55ms, and total acquisition time of 32 minutes. The T_1ρ-protocol was repeated on three volunteers on the same day for repeatability evaluation. This study was approved by the institutional review board (IRB) and all the volunteers consented before scanning.

SENSE reconstruction (31,32) of the fully-sampled data was utilized as reference. The coil maps, required by SENSE, were estimated using ESPIRiT (33) from the central k-space area.

Synthetic Phantom

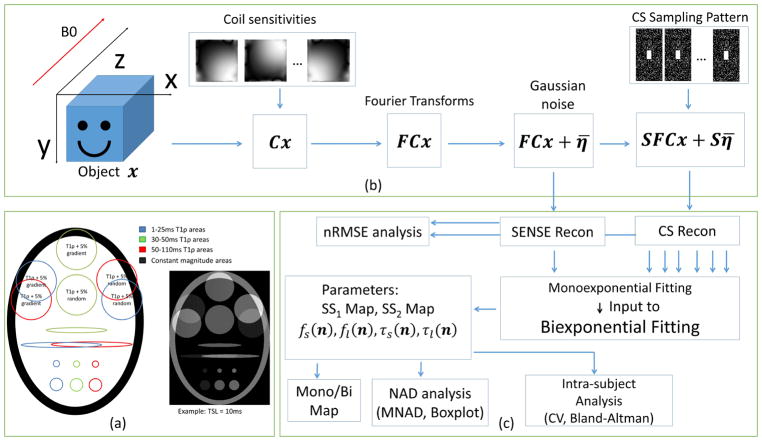
The utilized synthetic phantom is described in (30) and illustrated in Figure 1(a). It is composed of three T_1ρ relaxation areas with times: 1–25ms (blue), 30–50ms (green) and 50–110ms (red). Two areas partially intersect, generating a biexponential model (13). Other areas are purely monoexponential. As described in (30), the magnitudes in some areas are randomly selected, generating intersection areas with 10% dispersion from 50/50 in the fractions of short and long components of the biexponential.

Figure 1.

(a) Synthetic phantom utilized in the experiments, composed of three areas with different T_1ρ time ranges. The T_1ρ relaxation times were randomly selected from the ranges 1–25ms, 30–50ms, and 50–110ms, intersections generate a biexponential signal. (b) MRI acquisition model used for CS reconstructions, including coil sensitivities C, Fourier transform F, and k-space undersampling pattern S using Poisson disk with fully-sampled central area, also additive white Gaussian noise η̄. (c) Diagram of the process, including reconstruction, fitting, mono/biexponential detection, reconstruction and fitting error analysis and intra-subject analysis.

The k-space dataset was created by multiplying the phantom images by coil sensitivities, 4-coils were utilized, followed by 2D Fourier transform. White Gaussian noise was added to the data in k-space for the noisy experiment, with its standard deviation set to 17% of the mean signal amplitude, resulting in an acquisition SNR of 15dB (5.62 in linear scale). The acquisition SNR is defined as SNR = 10 log ||FCx||²/||η||², from the model: y = FCx + η with F and C described in equation [1] (not to be confused with image SNR, which is the visually observed noise in the reconstructed images and depends on the type of reconstruction).

Retrospective Undersampling

3D k-space data were retrospectively undersampled along the two-phase encoding dimensions (k_y and k_z) after applying 1D Fourier transform along the frequency encoding direction (k_x). As shown in Figure 1(b), the k_y-k_z data were undersampled following a 2D Poisson disk random pattern (34). The acceleration factor (AF) is defined as the ratio of total k-space samples by the number of measured k-space samples. A central rectangular k-space area was not undersampled and also used for coil sensitivity map estimation (31×15 for AF=2, 21×9 for AF ≥ 4, on a 128×64 fully-sampled captured datasets, and 63×63 for AF=2, and 41×41 for AF ≥ 4, on a 256×256 fully-sampled synthetic dataset).

CS Reconstruction Algorithms

Following (30), twelve different regularization functions are compared for CS. All the compared regularization functions are found in the image reconstruction literature, even though not tested for this specific problem, and are good candidates for this problem, as detailed below. The regularization penalties, described in Table 1, use l₁-norm with different sparsifying transforms, nuclear-norm (35,36) of the Casorati matrix representation of the image, i.e. low rank (LR) model, and the low rank plus sparse (L+S) model, where the nuclear-norm and the l₁-norm are combined (37). In the Casorati matrix, each row contains the magnetization signal of one particular voxel over TSL.

Table 1.

Different compressed sensing methods, their corresponding equation problem and minimization algorithm, a brief description, average number of iterations to converge and the average processing time to converge.

CS Method	Equation	Minimization algorithm	Transform/Dictionary	Avg. iterations	Avg. Time
TFD 1	[1]	FISTA -FGP	Temporal finite difference of order 1	40	514 sec
TFD2	[1]	FISTA -FGP	Temporal finite difference of order 2	60	684 sec
TFD3	[1]	FISTA -FGP	Temporal finite difference of order 3	80	691sec
STFD	[1]	FISTA-FGP	Spatial and temporal finite difference, spatial order 1 and temporal order 2	120	1298 sec
WAV	[2]	FISTA	3D Wavelet transform (2D+time) Daubechies 4, with 4 levels of decomposition.	43	1005 sec
PCA	[2]	FISTA	Unitary transform from temporal PCA of fully-sampled data	43	121 sec
KSVD	[2]	FISTA	Overcomplete temporal dictionary computed from fully-sampled data using KSVD	400	249 sec
EXP	[2]	FISTA	Overcomplete temporal dictionary of exponentials with 100 relaxation times between 1 and 300 ms	400	1290 sec
LR	[3]	Modified FISTA	Applied to a NyNz × Nt matrix formed with the reshaped NyNzNt × 1 vector.	38	194 sec
L+S	[4]	Modified FISTA	Same as LR, plus identity for l1-norm	80	218 sec
L+S SFD	[4]	Modified FISTA-FGP	Same as LR, plus spatial finite difference for l1-norm	120	837 sec
L+S WAV	[4]	Modified FISTA	Same as LR, plus 2D spatial wavelet for l1-norm, also Daubechies 4, with 4 levels.	55	1052 sec

The l₁-norm (16) regularized CS problems are posed as:

$$\widehat{\mathit{x}}=\underset{\mathit{x}}{\text{argmin}}{\Vert \mathit{y}-\mathit{SFCx}\Vert }_{\mathbf{2}}^{\mathbf{2}}+\mathit{\lambda }{\Vert \mathit{Tx}\Vert }_{\mathbf{1}},$$ [1]

or

$$\widehat{\mathit{x}}=\mathit{D}\underset{\mathit{u}}{\text{argmin}}{\Vert \mathit{y}-\mathit{SFCDu}\Vert }_{\mathbf{2}}^{\mathbf{2}}+\mathit{\lambda }{\Vert \mathit{u}\Vert }_{\mathbf{1}},$$ [2]

where x is a vector that represents the reconstructed image sequence, originally of size N_y × N_z × N_t, with N_y being the image size in the y-axis and N_z the size in the z-axis, N_t is the number of TSLs. y is a vector that represents the captured k-space, with original size of N_y × N_z × N_t × N_c, where N_c is the number of coils. The matrix C contains the coil sensitivities and F the Fourier transforms of each sensitivity-weighted image. The undersampling matrix S is a diagonal matrix, where the non-sampled k-space points have zeros in their diagonal positions; the respective elements in y are replaced by zeros as well. The squared l₂-norm or Euclidean norm, ${\Vert \mathit{e}\Vert }_{\mathbf{2}}^{\mathbf{2}}$, is the sum of the squared magnitudes, the l₁-norm, ||u||₁, is the sum of the magnitudes, and λ is the regularization parameter. The transform T and dictionary D in the regularization term are chosen as described in Table 1.

In Table 1, transform T contains the temporal finite differences (FD) of order 1, 2, and 3 for TFD1, TFD2, or TFD3. Those are temporal only high-order total variation (TV) (38–40). Also, T may contain the spatiotemporal FD (STFD) (40–42) set to order 1 spatially and order 2 temporally.

Fixed dictionary models for D are utilized for 3D wavelet transform (43), WAV in Table 1, or for overcomplete multiexponential dictionary D, EXP in Table 1 (44,45), with much more columns than rows. Learned dictionary models for D can be created using temporal principal component analysis (PCA) (46), using singular value decomposition (SVD) on the Casorati representation (23), or the K-SVD (47). In the case of the K-SVD, an overcomplete dictionary D is computed, instead of an orthogonal transform, as in PCA.

The LR reconstruction is defined as:

$$\widehat{\mathit{x}}=\underset{\mathit{x}}{\text{argmin}}{\Vert \mathit{y}-\mathit{SFCx}\Vert }_{\mathbf{2}}^{\mathbf{2}}+\mathit{\lambda }{\Vert \mathit{x}\Vert }_{\ast }.$$ [3]

In [3], ||x||_* represents the matrix nuclear-norm (35) where x is reshaped as a N_yN_z × N_t Casorati matrix, and the SVD is utilized at each iteration using the currently available reconstruction (48).

The L+S reconstruction (37) is given by:

$$\widehat{\mathit{l}},\widehat{\mathit{s}}=\underset{\mathit{x}}{\text{argmin}}{\Vert \mathit{y}-\mathit{SFC}(\mathit{l}+\mathit{s})\Vert }_{\mathbf{2}}^{\mathbf{2}}+{\mathit{\lambda }}_{\mathit{l}}{\Vert \mathit{l}\Vert }_{\ast }+{\mathit{\lambda }}_{\mathit{s}}{\Vert \mathit{Ts}\Vert }_{\mathbf{1}},$$ [4]

where x is decomposed into a sparse part s and a low rank part l, recombined by x = l + s. The low rank part uses of the nuclear-norm ||l||_*, while the sparse part uses of the l₁-norm with a specific sparsifying transform T, as listed in Table 1 for L+S reconstructions. This is also an overcomplete description of the images to be reconstructed (49). The highly correlated temporal part is represented by the LR component, while the temporally varying part, usually sparse in some spatially transformed domain, is represented by the sparse part. In (50), a similar combination of low rank and wavelet sparsity was studied for T₂ mapping.

Also following (30), and its supplemental material, the regularization parameters, λ or λ_l and λ_s, were adjusted in order to minimize ||x̂_λ − x_ref||₂ where x̂_λ is the CS reconstruction and x_ref the fully-sampled data SENSE reconstruction. The CS reconstruction was performed using fast iterative shrinkage-thresholding algorithms (FISTA) (51) and its modification coupled with fast gradient projection (FGP) (52) as the proximal operator. For L+S problems, the same algorithm can be used for s and l vectors. A modified FISTA for nuclear-norm is in (53). All methods stopped when ||x_i+1 − x_i||₂/||x_i+1||₂ < 10⁻⁵, or when i > 400, being i the iteration index. The methods K-SVD and EXP stopped by the maximum number of iterations, but their normalized update values, i.e. ||x_i+1 − x_i||₂/||x_i+1||₂, were close to the stopping tolerance.

Exponential Models and Fitting Algorithms

The T_1ρ relaxation is usually considered an exponential decay process. Typically, the model is described as:

$$x(t,\mathit{n})=\overline{a}(\mathit{n})\mathit{exp}\left(-\frac{t}{\tau (\mathit{n})}\right),$$ [5]

where x(t,n) is one particular voxel at 3D position n over TSL time t, ā(n) is a complex-valued magnetization, and τ(n) is the T_1ρ relaxation time at position n. However, magnitude-only models with positive real-valued a(n) and a constant component b, included due to residual noise, can also be considered, changing [5] to:

$$\mid x(t,\mathit{n})\mid =a(\mathit{n})\mathit{exp}\left(-\frac{t}{\tau (\mathit{n})}\right)+b.$$ [6]

The biexponential model can be written as:

$$\mid x(t,\mathit{n})\mid =a(\mathit{n})\left(f_s(\mathit{n})\mathit{exp}\left(-\frac{t}{{\tau }_s(\mathit{n})}\right)+f_l(\mathit{n})\mathit{exp}\left(-\frac{t}{{\tau }_l(\mathit{n})}\right)\right)+b,$$ [7]

Where 0 ≤ f_s (n) ≤ 1 and f_l (n) = 1 − f_s (n) are the fractions of short and long components at position n, respectively. Also, τ_s(n) and τ_l(n) are the T_1ρ relaxation times of the short and long components, respectively.

The biexponential T_1ρ parameters estimation, or simply fitting process, was done using non-linear least squares, using model [7], where the minimization was done using conjugate gradient Steihaug’s trust-region (CGSTR) algorithm (54). The CGSTR algorithm stopped at a maximum of 2000 iterations or normalized parameter update lower than 10⁻⁴. Biexponential estimation started with monoexponential fitting results, using model [6], classifying them as short (1–25ms) or long (25–300ms), depending on its estimated monoexponential T_1ρ relaxation time. Similar to (12), F-test was utilized for detecting mono/biexponential voxels. We follow the F-test method from (55), voxels were assumed to have biexponential behavior if F-ratio>5.14 (p-value=0.05) related to monoexponential. This means the sum of the squares (SS) of the biexponential fitting process is reduced significantly compared to monoexponential fitting. Also, both fractions (f_s (n) and f_l (n)) need to be higher than 10% in order to be a valid biexponential in these experiments. Figure 1(c) illustrates the process. The choice of 10% comes from tests with synthetic experiments (noisy). Together with F-test, it achieved the most correct detection of mono and biexponential voxels. More information about this is found in the online supporting material, and also within Supporting Figures S8 and S9, and Supporting Table S2.

Spatial filtering, used as a denoising over the regions of interest (ROIs), prior to the parameter estimation is sometimes helpful (56) to improve the quality of the estimated parameters. In this paper, we compare the non-filtered results with standard linear filter of spatially averaging of a 3×3 square of voxels (57).

Analysis of the CS Reconstruction and Fitting

The performance of the CS methods was evaluated according to the quality of the reconstructed images and the quality of the estimated biexponential T_1ρ parameters. Image reconstruction quality was assessed using normalized root mean squared error (nRMSE) against SENSE reconstruction of the fully-sampled data or the ground truth (for the synthetic phantom). The nRMSE is defined as:

$$\mathit{nRMSE}(\widehat{\mathit{x}},{\mathit{x}}_{\text{ref}})={\Vert \widehat{\mathit{x}}-{\mathit{x}}_{\text{ref}}\Vert }_{\mathbf{2}}/{\Vert {\mathit{x}}_{\text{ref}}\Vert }_{\mathbf{2}}.$$ [6]

The fitting process was applied only on each specific ROI. For in vivo knee cartilage, 5 ROIs were employed, following (13): medial femoral and tibial cartilages, lateral femoral and tibial cartilages and patellar cartilage. In those regions, the biexponential T_1ρ parameters, including T_1ρ times and fractions for short and long components, from CS reconstructions were compared against the parameters obtained from the reference reconstruction (and ground truth, when available).

The quality was assessed using normalized absolute deviation (NAD) of the parameters obtained in each voxel position n, given by:

$$\mathit{NAD}(\mathit{n})=\frac{\mid p(\mathit{n})-p_{\mathit{ref}}(\mathit{n})\mid }{(p(\mathit{n})+p_{\mathit{ref}}(\mathit{n}))/\mathbf{2}},$$ [7]

where p(n) is one of the four biexponential parameters (f_s (n), f_l (n), τ_s (n), τ_l (n)). Voxels in which any of the fractions were lower than 10% were excluded from the evaluation. As observed here and in (13), small fractions had inaccurate estimated T_1ρ parameters, even for fully-sampled images, leading to unrealistic NADs.

The errors in an ROI or sets of ROIs were quantized by the median of NADs (MNAD):

$$\mathit{MNAD}(\mathit{ROI})=\underset{\mathit{n}\in \mathit{ROI}}{\text{median}}\left(\frac{\mid p(\mathit{n})-p_{\mathit{ref}}(\mathit{n})\mid }{(p(\mathit{n})+p_{\mathit{ref}}(\mathit{n}))/\mathbf{2}}\right),$$ [8]

An MNAD of 0.1 corresponds to a median deviation of 10% on the estimated parameters compared to the reference, and it is more robust than the mean to measure the errors due to the instability of the non-linear least squares. Box plots are used for complete statistics about the NADs (median shows central tendency and quartiles shows the variability of the NADs).

Intra-subject repeatability is assessed using the coefficient of variation (CV), defined as CV=SD/M, being SD the standard deviation and M the mean of the median parameters of an ROI of two scans for the same volunteer. Bland-Altman plots were also used for selected methods.

RESULTS

Synthetic Phantom

The synthetic phantom results tell us how undersampling and noise affect the reconstruction quality and the biexponential fitting of the tested methods. This is only possible because the ground truth is available. It is important to state that fully-sampled SENSE reconstruction is not necessary the ground truth because it is corrupted by noise.

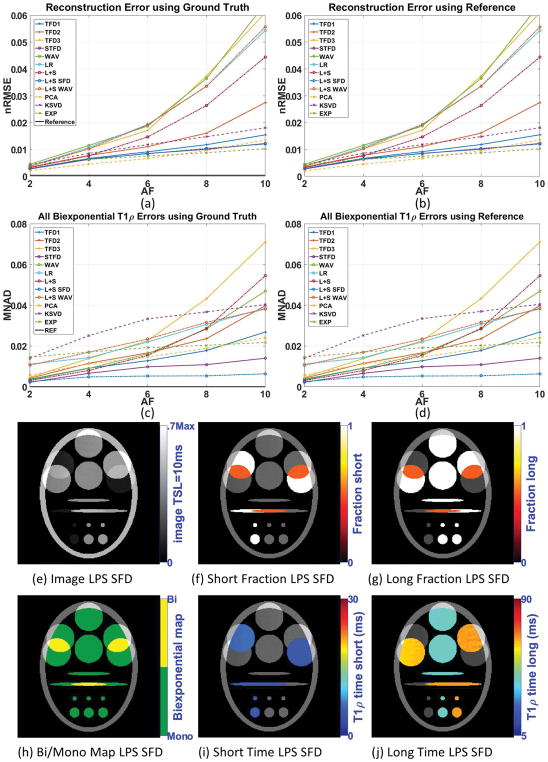
Figure 2(a) shows the reconstruction errors (nRMSE), and 2(c) shows the parameters error (MNAD) for the noiseless case when compared with the ground truth and 2(b) and 2(d) when comparing with the reference. When no specific biexponential parameter is mentioned, then all four parameters are being evaluated together. The Supporting Figure S1 provides individual MNAD for each parameter (f_s (n), f_l (n), τ_s (n), τ_l (n)). From Figure 2, we can infer that fully-sampled SENSE (coil combination of the fully-sampled data) is reliable to be used as reference when no noise is present, since its error is negligible. Comparing figures 2(a) and 2(c), as well as 2(b) and 2(d), it is observable that best reconstruction does not necessarily translate into best biexponential parameters. The MNAD for biexponential fitting is primarily affected by size of the reconstruction error, measured by nRMSE. However, the temporal shape of the reconstruction error is also important. One particular regularization function can, for example, reduce voxel magnitude for small TSL more than for large TSL, which will, consequently, affect the estimated relaxation parameters. More details on this, with an example, are included in the online supplemental information of this paper, with Supporting Figure S12. Some differences are also because nRMSE assesses the entire image, while MNAD assesses only a region of interest. A comparison of nRMSE at the entire image and only at ROI’s is included in the online supplemental information of this paper, with Supporting Figures S10 and S11.

Figure 2.

Results for synthetic phantom with no noise in the acquisition, including (a) reconstruction error (nRMSE) and (c) biexponential parameters error (MNAD) compared with ground truth, (b) reconstruction error (nRMSE) and (d) biexponential parameters error (MNAD) compared with reference for different acceleration factors (AF). Representative image and maps for L+S SFD using AF=6 are shown in (e)–(j).

In this experiment, methods L+S SFD and STFD were the best regarding biexponential parameters (providing good reconstruction quality too). Figures 2(e)–(j) show some visual results of L+S SFD.

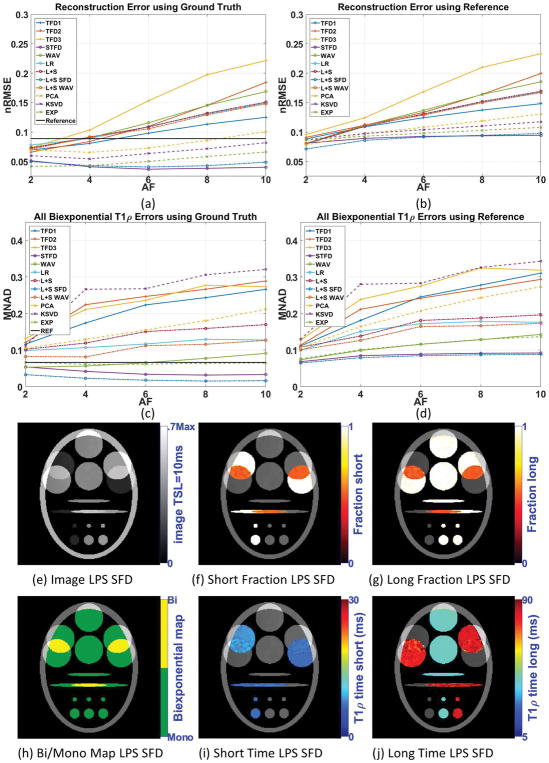
Figures 3(a) and 3(c) show the resulting reconstruction (nRMSE) and biexponential fitting errors (MNAD) for the synthetic noisy case when compared with ground truth, and 3(b) nRMSE and 3(d) MNAD when comparing with reference. Supporting Figure S2 details MNAD for each biexponential parameter. The results from Figure 3 show that fully-sampled SENSE reconstruction performed worse than some CS methods, such as L+S SFD, STFD, and EXP.

Figure 3.

Results for synthetic phantom with 15dB of noise in the acquisition, including (a) reconstruction error (nRMSE) and (c) biexponential parameters error (MNAD) compared with ground truth, (b) reconstruction error (nRMSE) and (d) biexponential parameters error (MNAD) compared with reference, for different acceleration factors. Representative image and maps for L+S SFD using AF=6 are shown in (e)–(j).

Comparing the results from Figure 2, with noiseless data, with the results from Figure 3, with noisy data, we can clearly observe that this level of noise can cause more errors in the fully-sampled reconstructed image (and its estimated relaxation parameters) than undersampling alone, with AF up to 10, in any noiseless CS reconstruction (and its estimated relaxation parameters).

Following the same observation of the noiseless case, good reconstruction not necessarily translates into good biexponential fitting. A clear example is the results with KSVD (compare figures 3(a) and 3(c)).

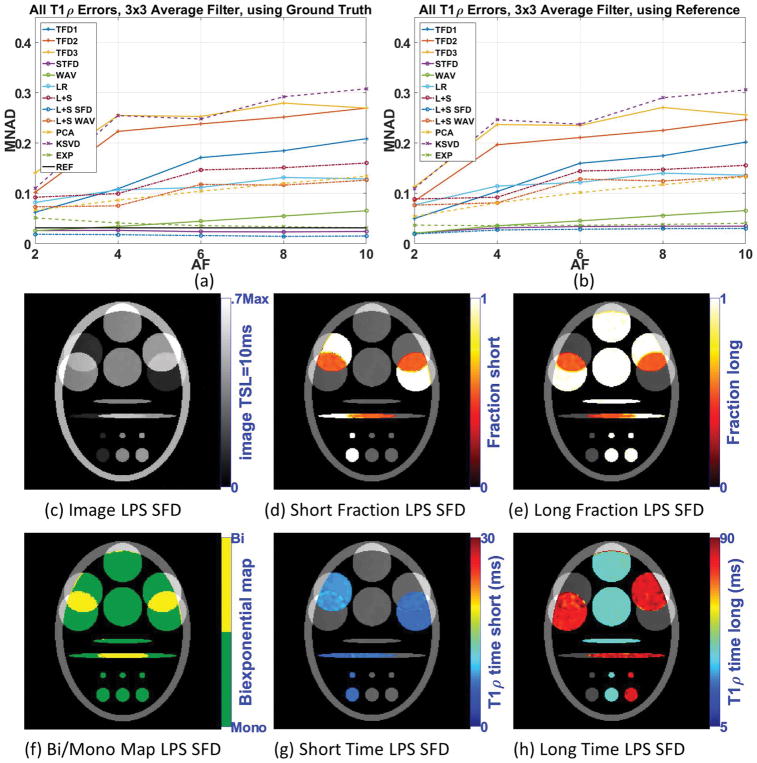
A common alternative to reduce noise and artifacts, improving the fitting results, is filtering prior to fitting. Figure 4(a) shows the biexponential fitting error (MNAD) after 3×3 averaging filter when compared with ground truth, and 4(b) when compared with reference. Supporting Figure S3 details the biexponential fitting error. Note that all methods have their MNAD reduced when filtering was utilized, including the reference. In general, the filtering reduces noise, but at the cost of reducing details of the biexponential maps (compare figures 3(e)–(j) and figures 4(c)–(h)). Another negative effect of filtering is the mixture of information of two different regions, especially at the boundaries. In Figure 4(j), for example, the filtering process artificially created biexponential voxels on the boundaries of regions with different monoexponential T_1ρ values. Nevertheless, methods such as L+S SFD and STFD performed better than the reference in terms of fitting results with 3×3 averaging filter in the synthetic experiments.

Figure 4.

Results for synthetic phantom with 15dB of noise in the acquisition, including (a) parameters error (MNAD) compared with ground and (b) compared with the reference, when 3×3 averaging filter is utilized, for different acceleration factors. Representative image and maps for L+S SFD using AF=6 are shown in (c)–(h).

In Vivo Knee Cartilage Data

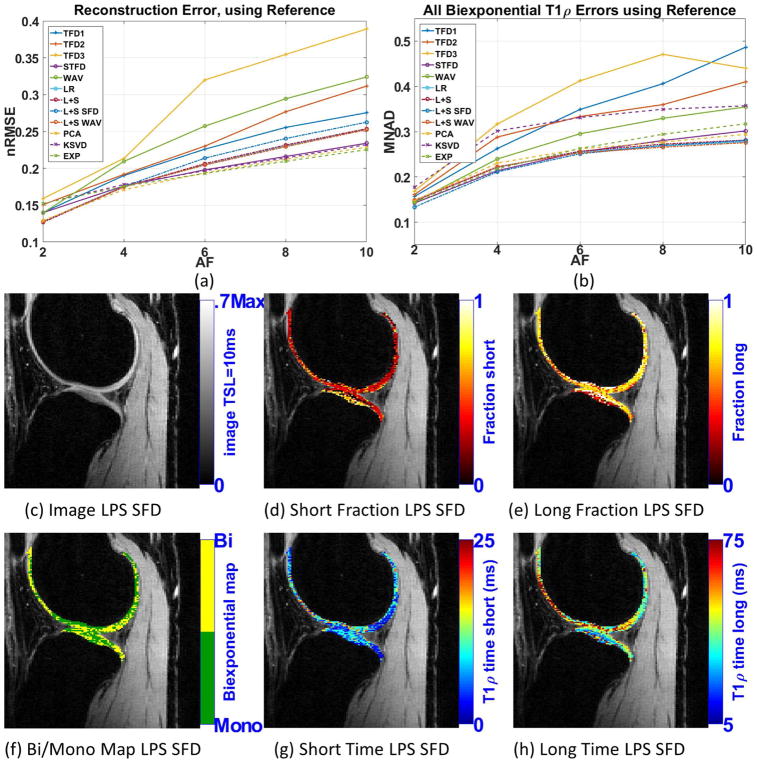
Our goal is to find suitable CS regularizations that perform well with in vivo knee cartilage. This region is challenging since it usually has small motion-related artifacts. Moreover, cartilage is curved and very thin. For this experiment, no ground truth is available. So, CS results were only compared with the reference (fully-sampled SENSE, possibly corrupted by noise and other artifacts).

Figure 5(a) shows the resulting reconstruction error (nRMSE) and 5(b) shows the resulting biexponential parameters error (MNAD). The detailed biexponential fitting errors are available in the Supporting Figure S4. Similar to the synthetic case, not all good CS reconstructions produced good biexponential parameters, KSVD is an example. Here, many CS methods had good results, with similar error levels, such as L+S SFD, STFD, L+S WAV, L+S, LR, PCA, and EXP. From synthetic noisy experiments, shown in figure 3(d), one can note that the best methods have similar MNAD when compared with the reference. Figures 5(c)–(h) show some visual results for L+S SFD at AF=4.

Figure 5.

Results for human knee cartilage, including (a) reconstruction error (nRMSE), and (b) parameters error (MNAD) compared with reference (SENSE), for different acceleration factors. Representative image and maps for L+S SFD using AF=4 are shown in (c)–(h).

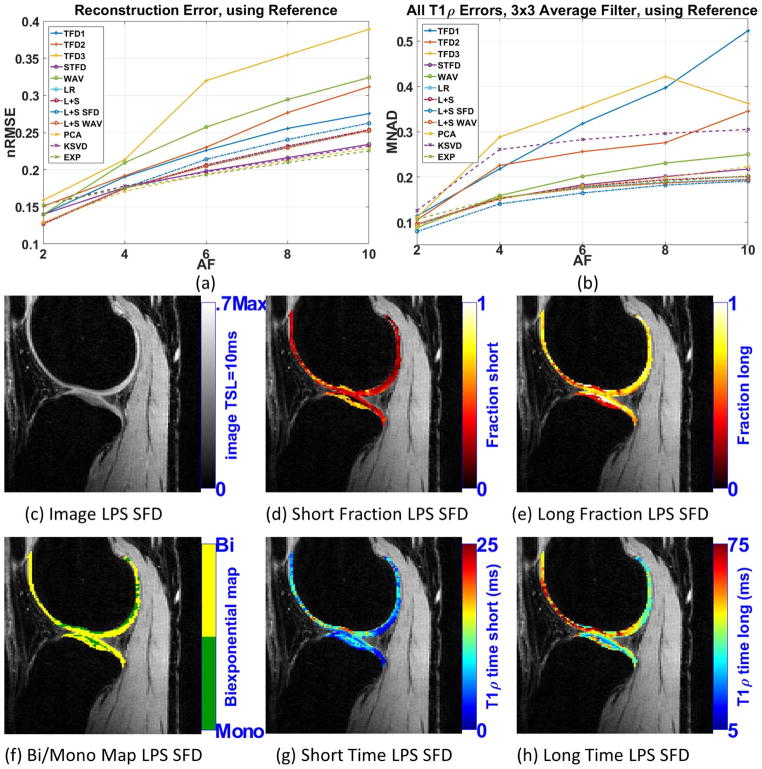
Figure 6(b) shows the MNAD for biexponential when 3×3 averaging filter is utilized. Supporting Figure S5 details this error for each parameter. As observed in the synthetic experiments, all the biexponential errors were reduced with pre-filtering. The use of pre-filtering gave some small advantage for L+S SFD, making it slightly better than the other methods: STFD, L+S WAV, L+S, LR, PCA, and EXP, which were all very good.

Figure 6.

Results for human knee cartilage, (a) reconstruction error (nRMSE), and (b) parameters error (MNAD) compared with reference (SENSE), for different acceleration factors, when 3×3 averaging filter is utilized. Representative image and maps for L+S SFD using AF=4 are shown in (c)–(h).

Figures 6(c)–(h) shows some visual results for L+S SFD at AF=4 when 3×3 averaging filter is used. We can clearly observe that biexponential maps look much less noisy than in figures 5(c)–(h), and perhaps more useful for further medical evaluation. Visual comparison with the reference can be seen in Supporting Figure S7.

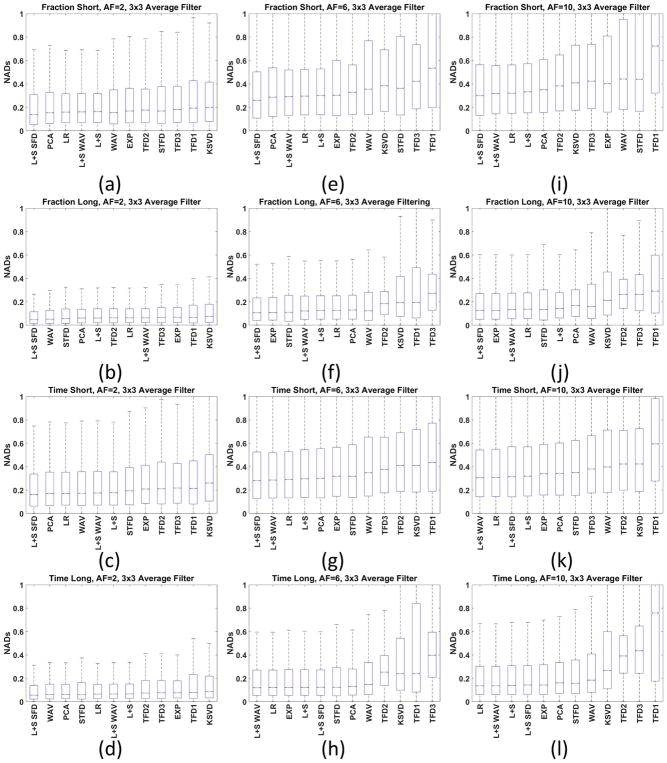
Figure 7 shows box plots for some specific AFs (2, 6 and 10) for the biexponential fitting results when filtering is utilized. The box plot shows much more information about the statistics of the NADs than only the median. Nevertheless, these results show that distributions of the NADs are very similar for all the best CS methods. It gives us support to exclude methods that did not perform satisfactorily: KSVD, TFD1, TFD2, and TFD3.

Figure 7.

Box plot of the NAD for all human knee cartilage datasets with 3×3 averaging filter for AF=2 (a) fraction-short, (b) fraction-long, (c) T_1ρ-short, (d) T_1ρ-long, (e)–(h) AF=6 and (i)–(l) AF=10. The box plot shows more information about the NADs than only the MNAD. The horizontal red bars represent the median of NAD (or NMAD), the blue box represent the central interquartile, where MAD values from percentile 25% to 75% are placed. The dashed dark lines represent the range of the data.

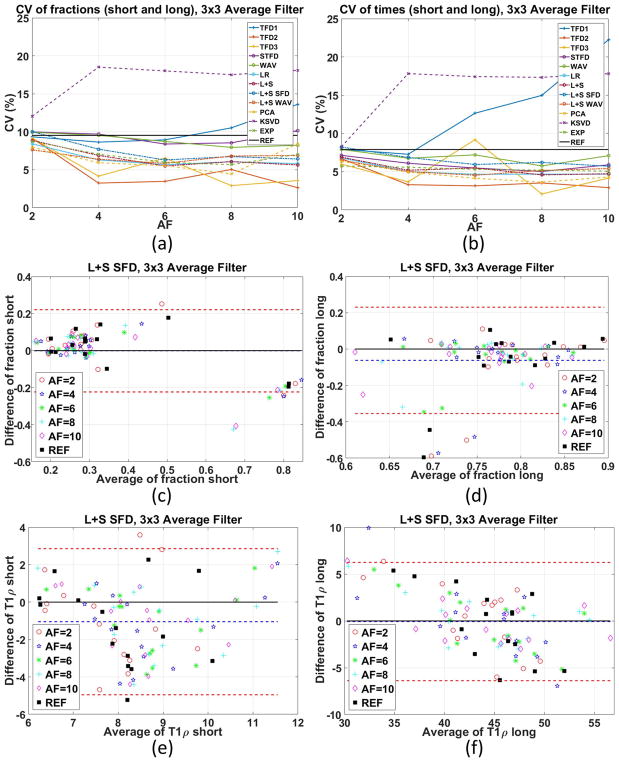
Figure 8 shows some intra-subject repeatability by the coefficient of variation and Bland-Altman plots for the method considered best so far, the L+S SFD, more details in Supporting Figure S6. Almost all CS methods achieved lower or similar CV than the reference, with some exceptions. This interesting result supports the use of CS for biexponential T_1ρ mapping.

Figure 8.

Coefficient of variation (CV), shown in percentage, of the different methods and acceleration factors with 3×3 averaging filter for (a) fractions, (b) times, considering two repetitions with each of the three volunteers. Bland-Altman plots for the L+S SFD method with 3×3 averaging filter for (c) fraction-short, (d) fraction-long, (e) T_1ρ-short, (f) T_1ρ-long considered the best in the previous experiment.

Overall Classification

In order to have an overall quantification of the results, we compute MNAD for all the results with synthetic noisy and in vivo datasets together, all compared to the reference. The first score, in Table 2A, is simply the MNAD of all biexponential errors (NADs), among 3 noisy synthetic datasets and 7 in vivo datasets, when no-filter is utilized. The resulting number provides us a median (normalized) parameter error of a particular method for the desired AF. The second score, in Table 2B, the MNAD was obtained when 3×3 averaging pre-filter was utilized.

Table 2.

A) Ranking the methods using its MNAD up to certain acceleration factor, for synthetic and in vivo datasets. Values lower than 0.2 (error of 20%) are bold-marked. B) Ranking the methods by its MNAD, when 3×3 averaging pre-filter is utilized, up to certain acceleration factor, for synthetic and in vivo datasets. Values lower than 0.15 (error of 15%) are bold-marked.

A. Median of normalized absolute deviation with no pre-filters
AF 2		AF4		AF 6		AF8		AF 10
L+S SFD	0.109	STFD	0.165	STFD	0.190	L+S SFD	0.207	L+S SFD	0.216
STFD	0.114	L+S SFD	0.166	L+S SFD	0.195	STFD	0.208	STFD	0.222
WAV	0.118	EXP	0.174	EXP	0.208	L+S WAV	0.231	L+S WAV	0.239
EXP	0.119	WAV	0.188	L+S WAV	0.222	EXP	0.234	LR	0.241
LR	0.131	L+S WAV	0.189	LR	0.226	LR	0.236	L+S	0.250
L+S WAV	0.132	L+S	0.192	L+S	0.228	L+S	0.241	EXP	0.251
L+S	0.133	LR	0.196	WAV	0.231	WAV	0.259	WAV	0.282
PCA	0.134	PCA	0.211	PCA	0.246	PCA	0.267	PCA	0.286
TFD1	0.141	TFD1	0.236	TFD2	0.303	TFD2	0.329	KSVD	0.352
TFD2	0.143	TFD2	0.262	TFD1	0.315	KSVD	0.342	TFD2	0.372
TFD3	0.155	TFD3	0.294	KSVD	0.316	TFD1	0.364	TFD3	0.403
KSVD	0.159	KSVD	0.295	TFD3	0.370	TFD3	0.428	TFD1	0.428
B. Median of normalized absolute deviation when 3×3 averaging pre-filter is utilized
AF 2		AF 4		AF 6		AF 8		AF 10
L+S SFD	0.056	L+S SFD	0.098	L+S SFD	0.114	L+S SFD	0.125	L+S SFD	0.131
WAV	0.062	STFD	0.103	STFD	0.123	STFD	0.136	STFD	0.147
STFD	0.065	EXP	0.111	EXP	0.127	EXP	0.137	EXP	0.148
PCA	0.078	WAV	0.113	WAV	0.145	L+S WAV	0.166	L+S WAV	0.172
EXP	0.079	L+S WAV	0.128	PCA	0.157	WAV	0.171	LR	0.173
LR	0.088	PCA	0.129	L+S WAV	0.159	LR	0.172	L+S	0.184
L+S WAV	0.090	L+S	0.130	LR	0.160	PCA	0.176	WAV	0.188
L+S	0.093	LR	0.140	L+S	0.165	L+S	0.177	PCA	0.198
TFD1	0.094	TFD1	0.179	TFD2	0.241	TFD2	0.260	KSVD	0.305
TFD2	0.096	TFD2	0.215	TFD1	0.261	KSVD	0.295	TFD2	0.317
TFD3	0.111	KSVD	0.256	KSVD	0.268	TFD1	0.317	TFD3	0.340
KSVD	0.120	TFD3	0.278	TFD3	0.328	TFD3	0.393	TFD1	0.409

From Table 2A, one can notice that a median error below 20% (bold marked) is expected when using AFs up to 6 with the methods STFD and L+S SFD. According to Table 2B, one can expect an MNAD below 15% up to AF of 10 when 3×3 averaging pre-filter is utilized with the methods STFD, L+S SFD, and EXP. In the literature (58), 5% error is considered acceptable for reproducibility for the monoexponential case. There are no similar error bounds for biexponential models. According to our experiments, the best results are for L+S SFD, which achieved 5.6% error at AF=2.

DISCUSSION

Recommended CS Methods

For AF=2, almost all CS methods produced good results, with low MNAD (0.109~0.159 without filtering, 0.056~0.120 with 3×3 averaging filter). As AF increases, fewer methods can provide low MNAD. We marked in bold letters, in tables 2A, 2B some suggested methods for each AF.

Our experimental results indicated that the use of 3×3 averaging filter provided the lowest MNAD for almost all CS methods. However, no matter if pre-filter is used or not, we observed that the CS methods STFD, L+S SFD, and EXP appeared among the best methods most of the time. This indicates that these three are the most suitable CS methods for accelerating biexponential T_1ρ mapping of the cartilage in the knee joint. This result is consistent with our previews experiments with monoexponential T_1ρ mapping in (30). On the other hand, methods L+S WAV, L+S, LR, PCA, and WAV also produced satisfactory results and could be considered.

Performance of the Regularization Penalties for Biexponential Fitting

Biexponential fitting is much more difficult and unstable than monoexponential fitting. In this case, the temporal shape of the reconstructed signal is extremely important (see more about this in the online supporting material of this paper, in Supporting Figure S12). Thus, the choice of regularizing penalty is important, since it affects how the signal will look like. Since noise strongly perturbs the fitting process, imposing spatial smoothness through regularization and/or spatial filtering prior to fitting produce positive effects. In this sense, the simple temporal finite differences, such as TFD1, TFD2, TFD3 did not perform well and their results were unstable.

The KSVD disappointed in some sense, even though it provided excellent reconstruction results, this did not translate into appropriate biexponential mapping. PCA performed better in this sense.

The STFD and WAV are both spatiotemporal models, imposing spatiotemporal correlation. The STFD performed very well, standing among the best methods in many tests. On the other hand, WAV did perform moderately well.

The EXP, which utilize a fixed overcomplete exponential dictionary, produced good results. It does not generate spatial correlation, so it was clearly benefited from the use of spatial pre-filters.

Some interesting positive results came from the LR and L+S penalties (L+S WAV and L+S SFD included). They all provided considerable results, especially with in vivo knee cartilage data. Moreover, the combination of low rank plus sparsity in the spatial finite difference domain (L+S SFD) provided the best results. Supporting Table S1 shows general qualification regarding the performance of the regularization functions for different aspects of the reconstruction and fitting.

We clearly observed that pre-filtering reduced mapping error. In part, because it reduced noise in the reference and in CS reconstructions, resulting in stable fitting and low MNAD. Even though there are better denoising filters (56) than standard 3×3 averaging, it still does a good job of reducing the errors. The drawback of filtering is the reduction of fine details in the biexponential mapping and possibly mixture of different regions.

Comparison with Previous Studies

As far as we know, this is the first study on the use of CS to accelerate biexponential T_1ρ mapping. In (13), reduced number of TSLs and GRAPPA (59) were tested for accelerated acquisition, up to AF=3. Most studies on accelerating general biexponential mapping apply to T₂ relaxation, where optimal or reduced time samples is searched (60,61), but no precise error per AF is given.

CS has been successfully utilized for monoexponential T_1ρ mapping. In (29) a combination of CS and autocalibration reconstruction (ARC) was utilized for knee cartilage T_1ρ monoexponential mapping errors close to 5%, or lower, for AFs around 2. In (25), three specific CS-like methods: integrating PCA and dictionary learning (PANDA), focal underdetermined system solver with PCA (k-t FOCUSS-PCA) and model-based dictionary learning (MBDL) were compared to accelerate brain and spine T_1ρ mapping up to AF of 4. T_1ρ relaxation errors between 8.9% and 12% were reported. In (26), a combined reconstruction with locally adaptive iterative support detection (k-t LAISD) and joint image reconstruction and sensitivity estimation in SENSE (JSENSE) method was proposed for knee cartilage T_1ρ mapping, with acceleration up to 3 and 3.5. In (27) blind compressed sensing (BCS) was applied to monoexponential T₂ and T_1ρ mapping of the brain.

Here, we provide a broad evaluation, using AF from 2, up to 10, comparing twelve CS methods, with and without pre-filtering, on 6 synthetic datasets and 7 in vivo human knee cartilage datasets for biexponential T_1ρ mapping. These results complement our previous results in (30) for monoexponential T_1ρ mapping. In order to keep all evaluations completely unbiased, we are not proposing or claiming any method of our own. All penalties appeared elsewhere in the literature for different applications, in the exact or similar form used here. The important novelty here is the evaluation of their performance for biexponential T_1ρ mapping.

Limitations of This Study and Future Directions

In our tests, the regularization parameters were selected to minimize l₂-norm of the difference between CS and the fully-sampled SENSE, essentially minimizing nRMSE. However, the ideal parameter would be the one that makes the reconstruction closer to the ground truth (unknown in practical cases). Therefore, how to choose the regularization parameter is still an open question. See more details on the criterion and procedure to choose the regularization parameters in the online supplemental information of (30).

In this study, we did not evaluate prospective undersampling. We hope to address this in the future, together with an automatic choice of the regularization parameter, when a fully sampled reference is not available.

It is also known that the ratio between short and long component/fraction affects the stability of the biexponential fitting (13,45). In the synthetic phantom study, the ratios are randomly dispersed by at most 10% around a 50/50 ratio and are free in real data sets. Performance of the methods with different components/fractions, especially for small fractions, and the stability of biexponential model will be addressed in future work.

The number of TSLs and their distribution are also relevant. Our choice was based on previous study (13) showing the best tradeoff between T_1ρ quality and scan time, but different distributions are possible. The use of different AFs in each TSL should also be investigated in the future.

Model-based reconstructions are promising approaches for monoexponential relaxation (62,63). It is not clear yet if they can be successful with biexponential models due to the instability and non-unicity of this inverse problem.

CONCLUSION

This study shows that CS can accelerate biexponential T_1ρ mapping of cartilage in the knee joint. Twelve different CS methods were compared, being the most indicated methods: L+S SFD, STFD, and EXP. In addition, the use of pre-filtering prior to T_1ρ fitting is recommended at the expense of spatial smoothing. These best CS methods performed satisfactorily for AFs up to 10, with error below 15%. The use of CS is a good alternative to make clinical studies with the biexponential model a viable approach.

Supplementary Material

Supp info

Supporting Table S1: Qualification of the methods according to their performance on different aspects.

Supporting Table S2: Some F_ratio values based on the choice of the p-value for the problem of detecting mono or biexponential voxels.

Supporting Figure S1: Details of the biexponential parameter errors (MNAD) for synthetic phantom with no noise in the acquisition: (a) fraction-short error (c) fraction-long error (e) T_1ρ-short error, (g) T_1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T_1ρ-short error, (h) T_1ρ-long error, compared with the reference.

Supporting Figure S2: Details of the biexponential parameter errors (MNAD) for synthetic phantom with 15dB of noise in the acquisition: (a) fraction-short error (c) fraction-long error (e) T_1ρ-short error, (g) T_1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T_1ρ-short error, (h) T_1ρ-long error, compared with the reference.

Supporting Figure S3: Details of the biexponential parameter errors (MNAD) for synthetic phantom with 15dB of noise in the acquisition when 3×3 averaging filter is used: (a) fraction-short error (c) fraction-long error (e) T_1ρ-short error, (g) T_1ρ-long error, compared with the ground truth; (b) fraction-short error (d) fraction-long error (f) T_1ρ-short error, (h) T_1ρ-long error, compared with the reference.

Supporting Figure S4: Details of the biexponential parameter errors (MNAD) for in vivo human knee cartilage: (a) fraction-short error (c) fraction-long error (e) T_1ρ-short error, (g) T_1ρ-long error, compared with the reference.

Supporting Figure S5: Details of the biexponential parameter errors (MNAD) for in vivo human knee cartilage with 3×3 averaging filter: (a) fraction-short error (c) fraction-long error (e) T_1ρ-short error, (g) T_1ρ-long error, compared with the reference.

Supporting Figure S6: Details of the coefficient of variations (CV) for intra-subject in vivo human knee cartilage with 3×3 averaging filter: (a) fraction-short (b) fraction-long (c) T_1ρ-short, (f) T_1ρ-long.

Supporting Figure S7: Visual comparison of some results of the knee cartilage, with and without filtering, for reference and L+S SFD with AF=2 and AF=6.

Supporting Figure S8: Illustration of the monoexponential and biexponential fitting for the knee cartilage dataset (medial).

Supporting Figure S9: Number of wrongly classified voxels as biexponential or monoexponential according to the choices of α_F, α_s and α_l for the utilized criterion.

Supporting Figure S10: Comparison of (a) nRMSE, (b) nRMSE for ROI only and (c) MNAD for the synthetic noisy phantom.

Supporting Figure S11: Comparison of (a) nRMSE for entire image, (b) nRMSE for ROI only and (c) MNAD with no filter and (d) MNAD with 3×3 averaging filter, for the in vivo knee cartilage.

Supporting Figure S12: (a) Ground truth, KSVD reconstruction and fitted biexponential curve, and (b) distribution of the reconstruction error over time.