Low Temperature Reaction Dynamics for the CH₃OH + OH Collisions on a New Full Dimensional Potential Energy Surface

Abstract

Is the rise of the rate constant measured in laval expansion experiments of OH with organic molecules at low temperatures due to the reaction between reactants or to the formation of complexes with the buffer gas?. This question has importance for understanding the evolution of prebiotic molecules observed in different astrophysical objects. Among these molecules methanol is one of the most widely observed, and its reaction with OH has been measured by several groups showing a fast increase of the rate constant under 100K. Transition state theory doesn’t reproduce this behavior and here dynamical calculations are performed on a new full dimensional potential energy surface developed for this purpose. The calculated classical reactive cross sections show an increase at low collision energies due to a complex forming mechanism. However, the calculated rate constant at temperatures below 100 K remains lower than the observed one. Quantum effects are likely responsible for the measured behavior at low temperatures.

Introduction

Among the more of 200 molecules detected in space, organic molecules are the most abundant ones of more than 4 atoms, and this makes that they are usually called complex organic molecules (COMs). Herbst and van Dishoeck ¹ defined COMs as those organic molecules with more than 6 atoms, but here we shall denote COM to any organic molecule independently of this number. These COMs have been detected in the interstellar medium (ISM) in many different objects ², and considered as prebiotic molecules. It is interesting is to follow their formation/destruction route from the original molecular clouds originating a star to the final planetary system, through protostellar and protoplanetary disks, etc. In many cases these molecules are present in very unfavorable environments, under UV radiation, in molecular outflows, etc, and it is therefore of crucial importance to understand their chemical evolution.

Formaldehyde³ and methanol⁴ were the first COMs detected in space and are among the most abundant ones. These molecules are efficiently formed by irradiation of CO-H₂ mixture ices ^5,6 and by successive hydrogenation of CO on dust grains ^7–10, but their formation in gas phase is typically neglected¹¹ because many of the sequential steps along their chemical formation mechanism present barriers impossible to overcome at the cold temperature of the ISM. The detection of these molecules in gas phase is not yet fully understood, because in cold regions, at about 10K, these species can not thermally desorb from ices, and they should pass to gas phase only after absorbing high energy cosmic ray or UV radiation. Molecules like methanol, which forms very strong hydrogen bonds, are not easily desorbed by UV absorption, and instead they break and only the photofragments go to gas phase, as recently measured^12,13. Therefore, if methanol is produced in ices, its photofragments can be the precursors to form back methanol¹³, or methanol itself could be the photofragment of a larger molecule still not found¹². In any case, it seems at present probable, that many of the COMs detected in space in gas phase, are formed in a complex route, involving reactions in ices and in gas phase.

Recent experiments for the reaction of methanol with hydroxyl radical using a Laval-nozzle expansion measured a fast increase of the reaction rate constant at temperatures below 100K¹⁴. These results open the gas phase route to form COMs and were confirmed by other experiments on the title reaction^15,16 as well as for some other molecules with OH^17–20. This gas phase reaction rate constant allowed to model properly the abundance of CH₃O radical observed in Barnard 1b¹⁶.

The CH₃OH + OH reaction yields two different products

$$C{H}_{3}OH+OH\to \{\begin{array}{ll}C{H}_{2}OH+H_{2}O\hfill & (R_{CH})\hfill \\ C{H}_{3}O+H_{2}O\hfill & (R_{OH})\hfill \end{array},$$ (1)

where R_CH and R_OH refers to the Hydrogen atom taken from CH₃OH, i.e., either one of the 3 H atoms of the CH₃ group to produce CH₂OH, or the hydrogen from the group OH to produce CH₃O, respectively. Hereafter we shall denote each of these two mechanism by R_CH (or CH₂OH) and R_OH (or CH₃O), whose potential energy barriers are ≈ 0.09 and 0.29 eV, respectively.

The increase of the rate constant at low temperature was initially explained by a tunneling mechanism within the transition state theory (TST)¹⁴. However, a theoretical study²¹ has shown that the imaginary frequency using by Shannon et al. ¹⁴ to estimate the tunneling rate was artificially too large, and that using a more realistic value yields reaction rate constants lower than the experimental values. Siebrand and co-workers proposed an alternative model, in which a methanol dimer is formed which then collides with OH giving rise to a OH-CH₃OH complex at energies below the OH + CH₃OH reactants threshold. This OH-CH₃OH complex can only decay towards products by tunneling through the reaction barriers. Recently, a competitive canonical unified statistical (CCUS) model was used to model the low and high pressure limits of this reaction²² and found that the fast increase at low temperatures could be explained only in the high pressure, somehow confirming the previous dimer model mechanism²¹.

However, a recent analysis by Shannon et al. ²³ showed that the proportion of methanol dimers in the Laval expansion is at most one order of magnitude lower than those required in the model of Siebrand and co-workers²¹ at the lowest temperature studied. However, some controversy about the dimer mechanism still remains^23,24. It is important to note, that it is crucial to determine if the increase of the reaction rate constant at low temperature is due to clustering of reactants (high pressure limit) or not, because at the low densities of the ISM such mechanism would not be possible. In addition to this interest, reactions with OH are important in atmospheric chemistry since it is the major oxidizing species in atmosphere and combustion²².

From the theoretical point of view it is of great importance to determine the accuracy of statistical theories, such as TST or CCUS, to study the reactivity at low temperatures, where quantum effects such as multidimensional tunneling in the deep regime may take place. The goal of this work is to develop a new full dimensional potential energy surface (PES) in which dynamical calculations on this reaction are performed to clarify the mechanism.

Ab initio calculations and analytical PES

To describe the reaction at low temperatures, a highly accurate ab initio method is needed (to describe properly long range interactions and reaction barrier heights) and many integration time steps to describe the slow dynamics. All this makes unaffordable the use of direct dynamics. A full-dimension PES then is needed.

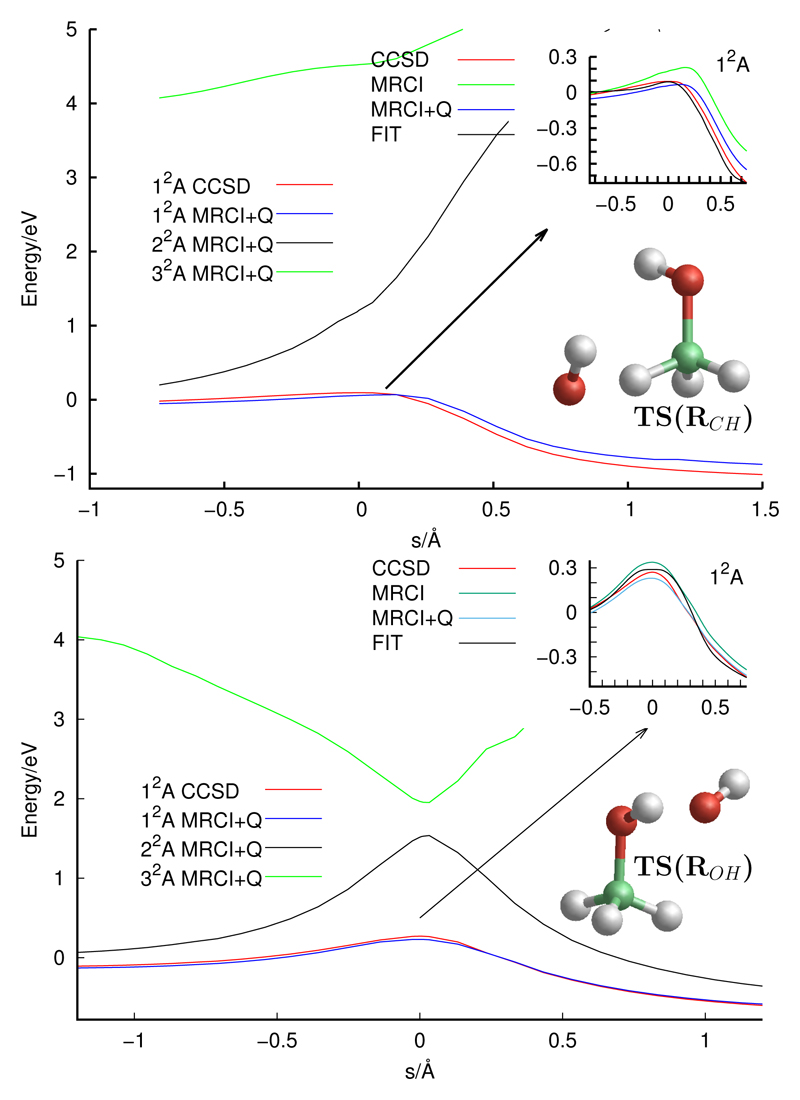
In this work, all the ab initio calculations were performed with the MOLPRO package²⁵. The explicitly correlated coupled cluster method including single and double excitations and with perturbative treatment of triple excitations, CCSD(T)-F12a, is an standard that is very well adapted to describe long range interactions. The explicitly correlated terms added in the F12 treatment²⁶ augment the conventional CI expansion by additional functions that included short-range pair correlation functions, improving the convergence toward the complete basis set limit. We use the ccpVDZ-F12 atomic basis set ²⁷, that keeps a compromise between a moderate size and a good accuracy. The Intrinsic Reaction coordinate (IRC) calculated with the CCSD(T)-F12a for the two reactions are shown in Fig. 1 and the stationary points obtained for this system are shown in the ESI†.

Fig. 1.

Intrinsic reaction coordinate (IRC) paths obtained with the CCSD(T)-F12a method and fitted analytical potential for the two reactions, R_CH (CH₂OH) in the top panel, and R_OH (CH₃O) in the bottom panel, of Eq. (1). MRCI-F12a+Q calculations of the first 3 electronic states are also shown for the two reactions. The inset shows the geometry of the transition state for R_CH and R_OH of energies 0.089 and 0.289 eV, respectively, for the fit PES. The keys of the figures, CCSD and MRCI-Q, correspond to CCSD(T)-F12a and MRCI-F12a+Q, respectively.

As noted previously²², at the R_OH barrier there is a rather high multi-reference character. Single-reference methods like CCSD(T)-F12a can present problems for the description of some reactions, and the T₁ diagnostic²⁸ allows to determine the multi-reference character: for open shell systems a value larger than 0.045 indicates that the system require a multi-reference method. The T₁ diagnostic has been analyzed along the two Minimum energy paths (MEP’s) calculated for the two reaction pathways of Eq. (1). It is found that for the R_CH reaction the T₁ diagnostic is below 0.03, while for the R_OH reaction in the vicinity of the barrier it reaches values of ≈ 0.05, indicating that in this case CCSD(T)-F12a is a limiting case. Something very similar was found by Gao et al. ²².

Explicitly correlated Multi-reference Configuration Interaction (MRCI-F12) calculations with the same basis set, have been performed along the R_OH Minimum Energy Path (MEP) obtained with the CCSD(T)-F12a for the first 3 electronic states, as shown in Fig. 1. The reference configurations were obtained with a state-averaged complete active space multi-configurational method (SA-CASSCF), optimized for the lowest 4 electronic states. To use the same active spaces in the CASSCF, all the calculations have been made without symmetry, using an active space of 15 orbitals. To avoid orbital flipping problems between the core and valence orbitals, all electrons have been correlated in the MRCI-F12 calculations. With this selection of states, the MRCI-F12 calculations involve a number of contracted (uncontracted) configurations of the order of 7.5 × 10⁶ (5.2 × 10⁸). Finally, a multireference Davidson correction technique (MRCI-F12+Q) was used in order to approximately account for the effects of higher excitations²⁹. The MRCI-F12+Q calculations for the first three electronic states along the IRC for the R_OH reaction are shown in Fig. 1. The MRCI-F12+Q and CCSD(T)-F12a results obtained for the ground electronic state is rather good, demonstrating that CCSD(T)-F12a is rather accurate even at the saddle point. The reason for the good behaviour of CCSD(T)-F12a resuls is that the second most important reference configuration corresponds to the excitation from the 13a²14a¹ to the 13a¹14a² configuration. These two orbitals belong to the valence space, and these two configurations correspond to the two Π states of OH subunit. The MRCI-F12 calculations take considerably longer time than the CCSD(T)-F12a calculation, and in this work we use the CCSD(T)-F12a method to calculate the PES.

The development of analytic fits for systems of 8 atoms is not a simple task specially to describe accurately reactions. The method of permutationally invariant polynomials of Bowman et al. ³⁰, based on the direct fit of the many body term, has been applied to systems up to 10 atoms and, for example, has been successfully applied to study S_N2 reactions ³¹ and water clusters ³². Another type of methods is based on the use of neural networks^33,34 or combinations of permutationally invariant polynomials and neural networks^35,36, which are able to efficiently optimize many non-linear parameters, allowing to describe many dimensions but with the cost of using many sampling points. All these methods are not directly applicable to treat the dynamics at low temperatures because for describing long range interactions properly the configuration space increases enormously. In this work we use a method recently proposed^37–39 which consists in dividing the electronic Hamiltonian in two terms as

$$H=H^{diab}+H^{MB}.$$ (2)

H^diab is an electronic diabatic matrix, in which each diagonal matrix element describes a rearrangement channel. In the case of ${\text{H}}_4^{+}$ and ${\text{H}}_5^{+}$ these terms were described by a triatomics-in-molecules method (TRIM)^37,38, which is an extension of the diatomics-in-molecule (DIM)^40,41, while in the case of H₂CO+OH those terms were described by force fiels ³⁹, as an extension of the reactive force field (RFF) approach⁴². This allows to describe polyatomic fragments rather accurately and long-range interactions can be included explicitly. In the supporting information† a detailed description of the reactive force field used to describe all the rearrangement reactive channels of Eq. (1) is presented. In this system, the dominant long range term is the dipole-dipole interaction between OH and CH₃OH which is included in the entrance channel. In the case of methanol the electric dipole vector goes from approximately the center of the CO bond towards the H atom of the hydroxyl group. This couples the orientation of OH with the torsion of methanol at long distances, which is expected to have a role in the dynamics.

In Eq. (2), H^MB is the many-body term, which is described by permutationaly invariant polynomials following the method of Aguado et al. ^43,44. The method and the fitting procedure is described in more detail in the supporting information†. More than 2 10⁵ CCSD(T)-F12a ab initio points have been used to fit this term. This many-body term improves the accuracy of the PES specially in the region of the reaction barriers, as shown in Fig. 1. For reaching such good description, the IRC of the fit was calculated and new ab initio points were calculated along it and along the normal modes orthogonal to it. This procedure was repeated iteratively until an acceptable error was achieved. Furthermore, a probe was set in all the classical trajectories presented below to determine the energy in the vicinity of the two saddle points: if the energy at the geometries corresponding to the TS is below the ab initio values, new points were added and the fit repeated, until none of these points were found. The resulting barrier of the R_OH reactions in the final fit is slightly higher than the CCSD(T)-F12a value, to get a better agreement with the MRCI calculations performed†. The long range interaction is also well described because the H^MB term vanish for internuclear distances longer than 10 bohrs.

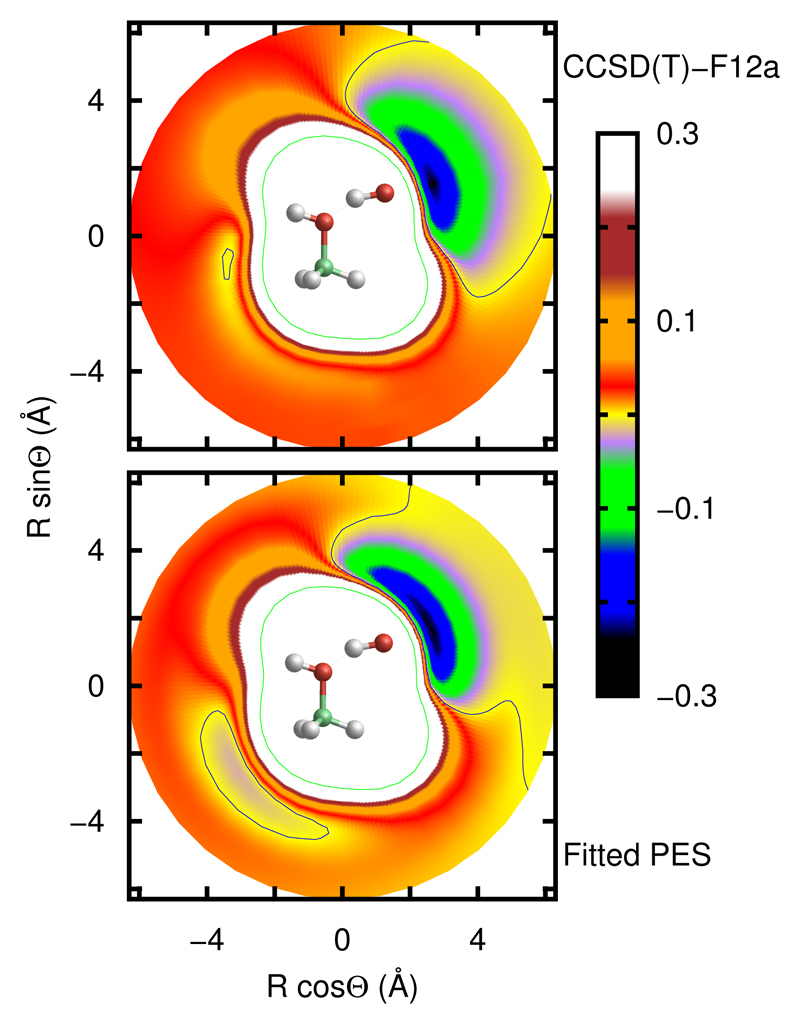
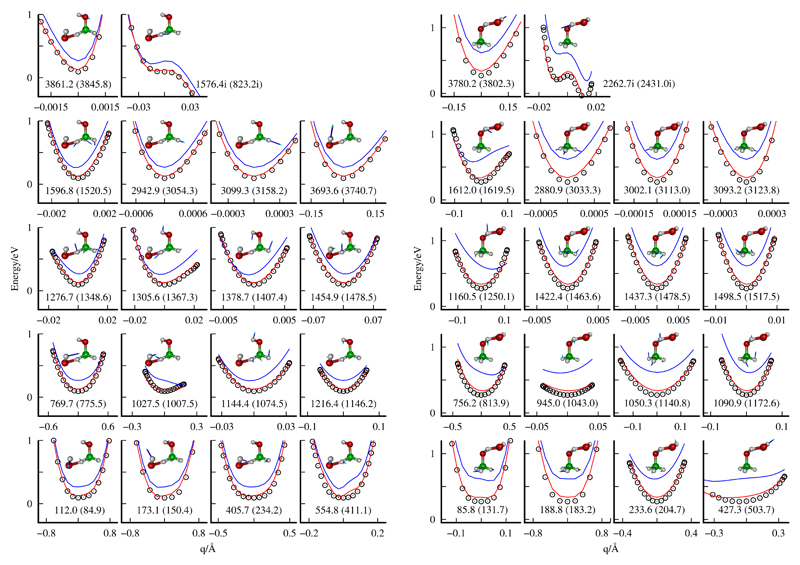
The error of the fit in different energy intervals and the procedures used to determine the geometries of the ab initio points are described in the supporting information†. The overall potential is smooth everywhere, and in Fig. 2 a contour plot of the PES in the entrance channel shows the potential well between the two reactants, comparing the fit with CCSD(T)-F12a calculations, which is closer to the TS for the R_OH mechanism than for R_CH, of high importance to explain the dynamical results presented below. The overall error of the fit is of the order of 84 meV below the zero of energy (see ESI†). However, this PES has a much higher accuracy to represent the long range of the interaction and at the transition state regions of the two reaction mechanisms. The cuts along the normal coordinates for each vibration mode at the saddle points of the two reaction mechanisms are shown in Fig. 3, showing an excellent agreement. These two aspects, long range and transition state regions, are the main factors determining the dynamics at low temperatures. For example, the available kinetic energy increases at the wells and the qualitative the behaviour of the dynamics in these regions is not expected to vary significantly. We therefore conclude that the present PES is well suited to represent the reaction dynamics at low temperatures at a semiquantitative level.

Fig. 2.

Contour plots of the Ab initio (top panel) and fit (bottom panel) PES’s corresponding to the geometry of the deeper well in the CH₃OH + OH entrance channel. CH₃OH and OH are kept at their equilibrium geometries. The inset molecular model correspond to the geometry of the minimum of the potential. Energy is in eV.

Fig. 3.

Monodimensional cuts along the normal coordinates, q_i, obtained at the saddle points of the R_CH (left panels) and R_OH (right panels), reactions, obtained with the CCSD(T)-F12a method. Points correspond to CCSD(T)-F12a, blue lines to the RFF and red lines to the full analytical PES. The insets present each normal mode, and the frequency of the full PES (ab initio) are also indicated (in cm⁻¹).

Dynamical results

The zero-point energy (ZPE) of the reactants are 0.232 and 1.484 eV, for OH and CH₃OH, respectively, in the harmonic approximation (HZPE), much higher than the height of the two reactions barriers, of 0.089 and 0.289 eV for R_CH and R_OH, respectively. These values were calculated by diagonalizing the Hessian matrix obtained from the analytical fit at the corresponding stationary points. To account for anharmonic effects, we have calculated the exact vibrational eigenvalues of OH, leading to a anharmonic ZPE of 0.229 eV. For methanol, exact eigenvalues are not calculated, and instead a path-integral molecular simulation is performed on the fit for the methanol using normal coordinates at 1 K and 65536 beads. After 2 millions of steps, the average energy is ≈ 1.443 eV, which is used as the approximated anharmonic ZPE of methanol. These anaharmonic ZPE are used as a reference to chose the initial conditions as described below.

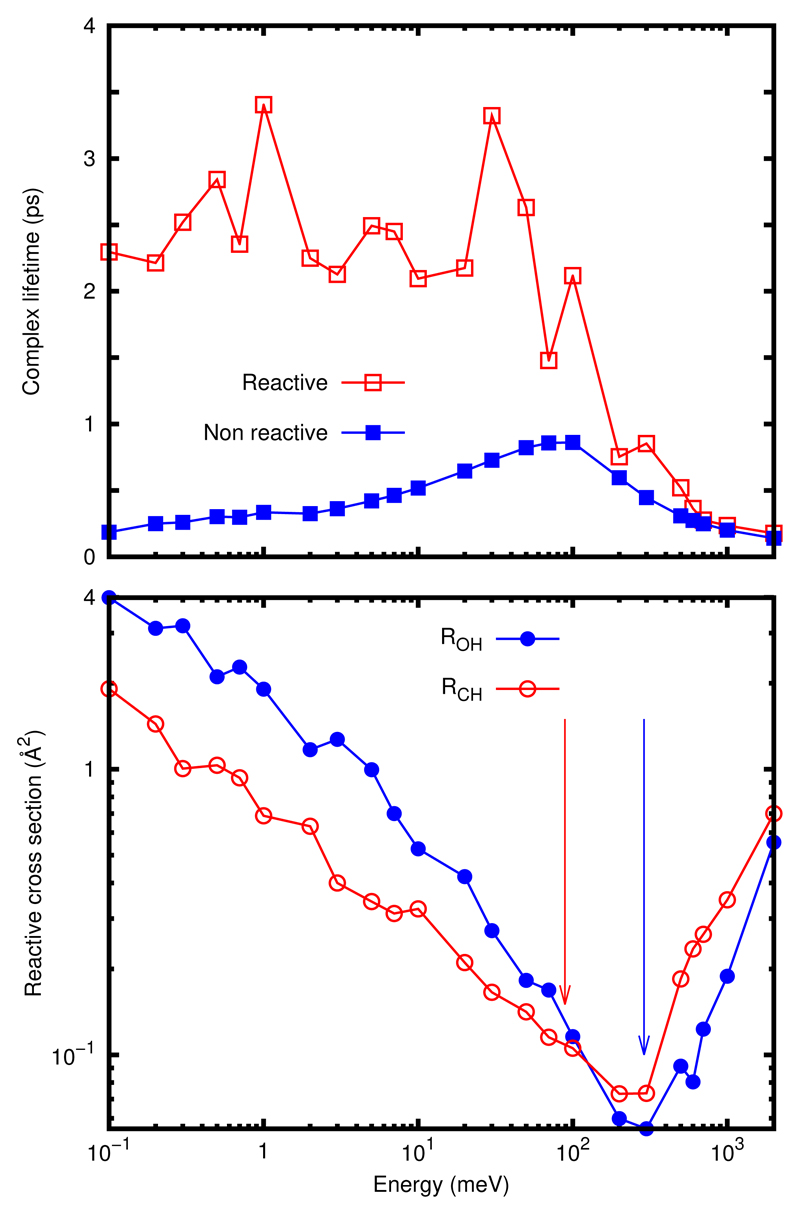
The initial conditions for the quasi-classical trajectory (QCT) calculations are calculated for the ground rovibrational state of the reactants using the adiabatic switching method^45–48 and selecting one trajectory, of 0.232 and 1.445 eV for OH and CH₃OH, respectively, in order to warranty that the initial vibrational energy is constant for all the trajectories. The reactive cross section at fixed collision energies has been calculated for the title reactions, as described in the ESI†and shown in the bottom panel of Fig. 4.

Fig. 4.

Bottom panel: Cross section for the OH(v=0,j=0)+ CH₃OH(V=0,J=0) for the reactions R_CH and R_OH a s a function of the collision energy in meV. Top panel: average lifetime (in ps) of the collision complex for non reactive and reactive trajectories, in this last case for the two reaction channels R_CH and R_OH together.

For the two reactions, the cross section decreases with decreasing collision energy, from 2 eV down to approximately 0.1 eV, close to the top of the two barriers marked with arrows in Fig 4. In this high energy interval, the reaction is fast and direct, and the cross section for R_CH is larger than for R_OH, simply because the impact parameter is larger for the CH₃ group than for OH.

At collision energies below 100 meV, below the top of the two barriers, the situation changes: the cross section for R_OH becomes larger than for R_CH. At these lower energies the reaction is no longer direct, and starts forming a long-lived complex. The reaction probability is rather low in the two cases, and the reason why cross section in the two reactions increase is due to the increase of the maximum impact parameter: at low energy the long-range dipole-dipole interaction is capable to reorient the two reactants while they approach, converting translational energy to rotation. The system is then trapped in the well of Fig. 2, similarly to what was reported for the H₂CO+OH reaction ^39,49. During the lifetime of the collision complex the system orbits around the entrance channel well, and the system finds more easily routes towards the R_OH barrier, closer to the well, than the barrier for R_CH. This explains why the cross section for R_OH is higher, even in the case that its barrier is higher. The formation of the CH₃O as the major product at low energies through R_OH reaction is consistent with its detection¹⁴ by laser-induced fluorescence at a rate consistent with the disappearance of CH₃OH.

The collision complex lifetime (see ESI†) as a function of energy is shown in the top panel of Fig. 4 for reactive and non-reactive trajectories separately, showing a remarkable difference below the top of the barrier: while the lifetime of reactive trajectories increase up to 2-3 ps, with oscillations, the inelastic collision lifetimes decrease. This seems to indicate that those trajectories leaving enough time in the complex reach products more easily than reactants. The oscillations of the lifetime for the reactive collisions could be attributed to tunneling bottlenecks, similar to classical resonances as those reported for similar reactions like OH + F^50–52, which mimic quantum resonances that can be characterized for this last triatomic system. In that case, those resonances appeared when the OH(j=0) reactant collides with methanol, acquiring a rotational excitation. When the rotationally excited OH(j>>) tries to fly back to reactants it cannot completely dissociate because the translational energy is insufficient to reach them. Thus the two reactants come back again generating large amplitude vibrations, associated to roaming trajectories ^53–56. Those trajectories explore regions far from the IRC, where anharmonic effects are high. This allows the energy transfer between the reaction coordinate and orthogonal modes, explaining why there are reactive trajectories with initial collision energies below the TS for the two reactions.

The use of classical methods for low energy collisions may be questionable, since they present the well know ZPE leakage. This effect would be very important in the channel of the reactants, for which the available kinetic energy to dissociate is very small, and any energy going to or coming from the methanol or OH would change the energy content significantly. This makes, in general, that the available phase space increases, or equivalently the density of states of reactants increases. This produces an increase of the inelastic cross section. This effect could be corrected by eliminating those trajectories not satisfying ZPE requirements, or more sophisticated methods like gaussian binning^57,58. This correction would decrease the inelastic cross section and, therefore, an increase of the reactive cross section, leading to better agreement with experimental data presented below.

This ZPE leakage problem it is not expected to play a fundamental role here, because as in the OH + F collision mentioned above^50–52, the energy transfer mainly affect the rotational energy, which occur via the long-range dipole-dipole interaction. As in the OH + F case^50–52 it is expected that the resonant structure will be qualitatively reproduced by these QCT calculations. However, quantum effects are expected to increase the collision complex lifetime what could lead to a larger reactivity”

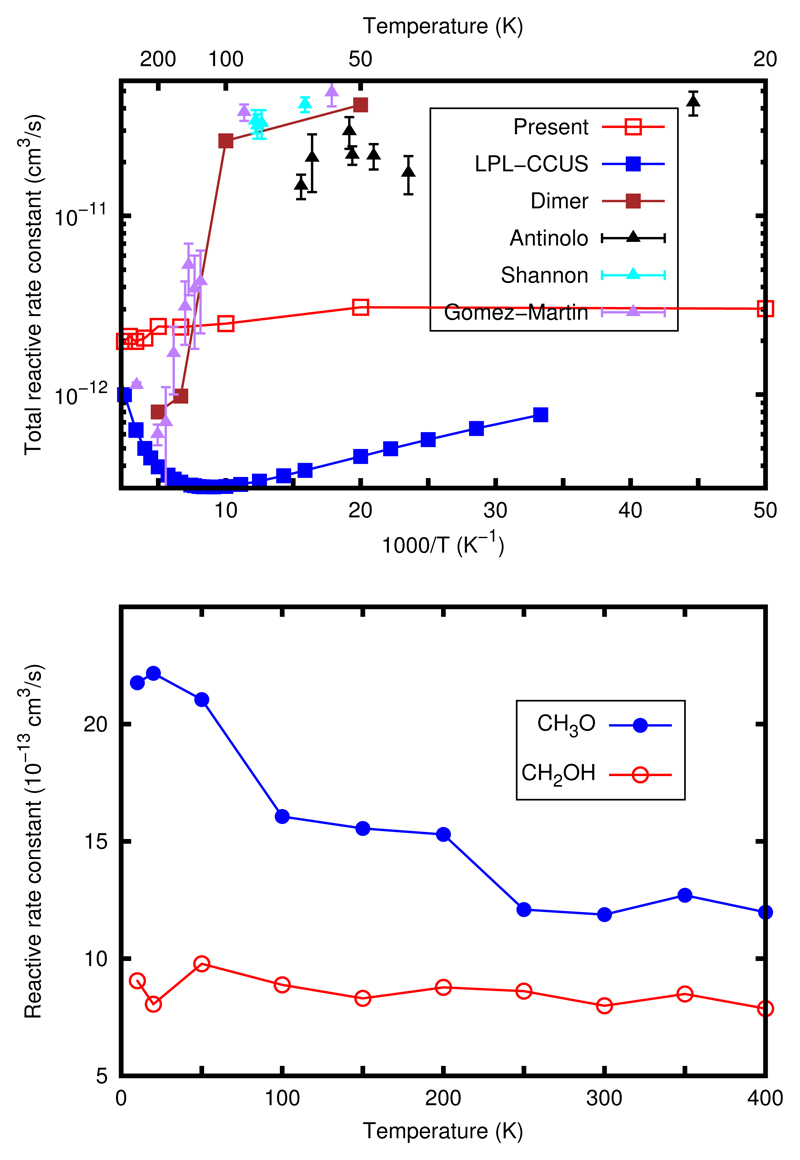
The reaction rate constants have been also calculated for the ground vibrational state of reactants (see ESI†for details) and they are shown in the bottom panel of Fig. 5. The rate constant for R_OH reaction is larger than for R_CH confirming the results discussed above after average over collision and rotational degrees of freedom. The increase with decreasing temperature is however small, being more important for R_OH reaction.

Fig. 5.

Bottom panel: Reaction rate constants for the OH(v=0)+ CH₃OH(V=0) for the reactions R_CH and R_OH as a function rotational and translational temperature. Top panel: Total reaction rate constant compared to the theoretical statistical model in the low pressure limit (LPL-CCUS) of Gao et al. ²², the CH₃OH dimer model of Siebrand et al. ²¹, and the experimental results of Shannon et al ¹⁴, Gomez-Martin et al ¹⁵ and Antiñolo et al ¹⁶ as a function of 1000/T.

In the top panel the total reaction rate constant, R_OH + R_CH, obtained here is compared with the available experimental data^14–16, as a function of 1000/T. Our results exhibit a significant increase, about a factor of 8, with respect to the low pressure semiclassical results (LPL-CCUS) of Gao and co-workers²², which also show a rise of the rate constant with decreasing temperature. Since the barrier heights used in this work are slightly higher than those of Gao and co-workers²² this difference in the magnitude is attributed to a non-IRC dynamics mechanism occurring at low temperatures. However, the classical trajectories results remain lower than the measured one, showing that something else is still missing.

In Fig. 5 the results of the methanol dimer model of Siebrand et al. ²¹ it is also shown for comparison, showing an excellent agreement with the experimental results. This dimer model presents some analogies with the present study, because when the OH collides with the methanol dimer it produce the CH₃OH-OH complex. The difference is that this CH₃OH-OH complex is formed at energies below the reactants asymptotic energy yielding CH₃OH + OH. This makes that the CH₃OH-OH complex can only disappear by tunneling towards products. The excellent agreement of the methanol dimer model relies on the asumption of a very high dimer formation probability of 30 %. The formation of clusters in CRESU experiments is known since its first development⁵⁹, and its contribution it is usually estimated by analyzing the effect of the pressure on the rates: the partial pressure of reactants chosen to evaluate the rate is that at which the reaction rate constant varies linearly with pressure. This study was done in the experimental studies of the values presented in Fig. 5. Even more, in a more recent study, Shannon et al. ²³ stablish an upper limit for the dimer probability of at most 5%. This experimental value stablish an upper bound to the effect of the dimer on the measured reaction rate constant. We therefore conclude that the main reason for the rise of the measured rate constant is not the dimer mechanism, even when it may have a relative effect in the quantitative value to be added to the error bars. Since the complex lifetime is expected to increase when quantum effects are considered, tunneling is expected to compete with the rotational predissociation mechanism yielding back to reactants. This would explain the rise of the rate constant at low temperatures, and simulations including quantum effects are now in progress.

Conclusions

In this work a full dimension analytical fit for the CH₃OH + OH reaction has been developed, based on accurate CCSD(T)-F12a calculations. This PES describes accurately the long-range and the IRC for the two products, CH₂OH and CH₃OH, thus been adequate to study the reaction dynamics at low temperatures.

The reaction dynamics is studied using a QCT method. It is found, that the cross section for the reaction towards the two products, CH₂OH (R_CH) and CH₃O (R_OH), increase with decreasing energy below their corresponding saddle points. This is explained by a complex forming mechanism, in which roaming trajectories following a non-IRC path are able to overcome the reaction barrier because of important anharmonic effects, which couple the reaction coordinate to the perpendicular modes.

Morover, it is also found that the cross-section yielding CH₃O products is higher than that for CH₂OH, even when it has a higher barrier. This is explained by the proximity of the geometry of the well in the reactants channel to the TS(R_OH) connected to CH₃O products. However, between the CH₃OH-OH well and the TS(R_CH) (yielding CH₂OH products) there is a barrier which makes more improbable this reaction mechanism. This results seems in agreement with the experimental data of Shannon et al. ¹⁴, in which CH₃O products were detected, while CH₂OH not. Even when a more quantitative experimental estimation of the products braching ratio is still needed, these results allow to explain the detection of CH₃O in space while CH₂OH has not been detected yet, as discussed previously¹⁶.

The reaction rates have also been calculated below 100 K, and the present QCT calculation do not show the increase of the experimental values. On the contrary the semiclassical LPL-CCUS results in the high pressure limit ²² and the results obtained in the dimer model²¹ do agree with the experimental rise of the reaction rate at low temperature. However, in this dimer model a 30% of dimers in the laval expansion is needed, while a more detailed recent experimental study less than 5% is formed²³. This discrepancy makes necessary to confirm the CRESU results using other techniques, such as cross-beam experiments at this low energies ⁶⁰).

From the theoretical point of view it is also needed to confirm if the rise of the rate is possible at low temperatures. For doing that, we consider necessary to include quantum effects in simulations, such as tunneling and zero point energy, which are important at this low temperatures. By considering ZPE effects the complex lifetime is expected to increase simply because the number of open levels of reactants decreases significantly. Increasing the lifetime would also increase the efficiency of the tunneling, and hence of the reactions. It is well known that the Ring-polymer Molecular dynamics method^61–65 (RPMD) is well adapted to include such quantum effects, and preliminary calculations performed with a recently proposed direct-RPMD formulation ⁶⁶ indicates that for some RPMD trajectories run at 100K in the title reaction, the collision complex lives more than 100 ns. This clearly show the complexity of those calculations, now in progress. The present full dimension PES will therefore allow to perform dynamical calculations with the RPMD and other methods to unravel the discussion on the title reaction.

Supplementary Material

† Electronic Supplementary Information (ESI) available: [details of any supplementary information available should be included here]. See DOI: 10.1039/b000000x/