Dynamic Switching of Helical Microgel Ribbons

Abstract

We report on a microscopic poly(N-isopropylacrylamide) hydrogel ribbon, coated by a thin gold layer, that shows helical coiling. Confined swelling and shrinkage of the hydrogel below and above its characteristic volume phase transition leads to a temperature actuated reversal of the sense of the helix. The extent and the shape of the winding are controlled by the dimensions and mechanical properties of the bilayer ribbon. We focus on a cylindrical helix geometry and monitor the morphing under equilibrium and nonequilibrium conditions, that is, when the temperature changes faster than the volume (millisecond range). For slow temperature variations, the water release and uptake follow the equilibrium transition trajectory determined by the time needed for the diffusion of water into and out of the microscopic gel. Much faster variations of the temperature are accomplished by internal heating of embedded gold nanorods by IR-light irradiation. This causes elastic stresses that strongly affect the motions. This method enables well-reproducible deviations from the equilibrium transition path and allows us to control rather precisely the spatiotemporal transformation in a cyclic repetitive process. Actuation and response are sensitive to small variations of temperature and composition of the aqueous sol in which the gel is immersed. The principle as described may be used to detect specific analytes that bind either to the surface of the gold layer or within the gel and can modify the interaction between the water and the gel. The reported nonequilibrium morphing implies that the system dissipates energy and may also be able to perform work as required for a microscopic motor.

Hydrogels whose constituent polymers are characterized by a lower critical solution temperature in water are known to undergo a volume phase transition. The gel collapses reversibly when either the temperature is raised or the solution conditions are changed (pH, ionic strength, etc.).^1,2 Depending on the geometry of the hydrogel body, such objects can morph between different shapes.³⁻⁹ Applications have been explored widely, exemplarily for encapsulation,⁵ drug delivery,¹⁰ tissue engineering,¹¹ and microfluidics.¹² Furthermore, feedback loops have been proposed for self-regulating chemical micro reaction systems.¹³ Repetitive volume changes offer intriguing perspectives to design micro swimmers and other locomotors, as has been demonstrated theoretically^14,15 as well as by a chemically fueled microgel walker.¹⁶ Recently we have realized experimentally a light driven morphing microswimmer. The principle is based on the ability of microscopic hydrogel objects to undergo complex large amplitude motions when the volume change is coupled to distortion modes under nonequilibrium conditions.¹⁷ The latter point is important when a repetitive cyclic deformation is driving a directed motion and enabling the microsystem to perform work. By a proper combination of different deformation modes a cyclic process with forward and backward strokes can be distinguished. As a result at small Reynolds numbers directed rotations and even forward movement can be effectuated. This was demonstrated by a helical hydrogel ribbon whose helix pitch and diameter oscillated due to light-controlled heating from inside. Temperature jumps were induced by heating embedded gold nanorods via irradiation at λ = 808 nm, the maximum of the longitudinal plasmon resonance band.

In this work we report helix reversal of a microscopic poly(N-isopropylacrylamide) hydrogel ribbon, poly(NIPAm), coated by a thin gold layer and affected by the volume phase transition. Particular emphasis is put on the large amplitudes and large rates of the changes that can be achieved, as well as on a comparison of the changes under equilibrium and nonequilibrium conditions. Like in our previous report, fast temperature rises are achieved by heating the microgel from inside with the help of embedded gold nanorods that convert IR light efficiently to heat. Subsequent fast cooling is enabled by the small dimensions of the ribbon kept in water at constant temperature. The volume change of the hydrogel layer is triggered by deswelling and reswelling and thus diffusion controlled. Hence its rate is several orders of magnitude smaller than the temperature change, and the resulting deformations require milliseconds to seconds. As a consequence, the helix deformation can take place under nonequilibrium conditions. We will demonstrate the enormous sensitivity of the deformations rate and amplitude that can be achieved. Next we explore the interplay between geometry and swelling properties of the microscopic bilayer structure comprising a hydrogel layer. Finally we shortly discuss the potential of these responsive systems for sensing applications.

Results and Discussion

Shape Selection through Misfit Strain

The helices are formed from a bilayer ribbon consisting of a poly(NIPAm) hydrogel layer on which a 2 nm thick gold layer was sputtered. The dimensions were length L = 80 μm, width w = 5 μm, and height h = 1 μm. Upon swelling in water, expansion and stretching of the gel layer are restricted by the gold skin, which itself can be stretched barely. Hence, the structure is a bilayer ribbon in which one layer expands relative to the other.¹⁸ As a consequence, swelling and deswelling of the hydrogel causes stresses which, in turn, lead to bending of the bilayer. The bilayer microribbon has been prepared by cross-linking polymerization of NIPAm in DMSO solution in micromolds as described elsewhere¹⁷ (see Supporting Information). In that situation swelling at low temperatures (<30 °C) causes concave bending toward the gold layer and deswelling at high temperatures (>32 °C) causes convex bending. Deswelling is effected either by warming the surrounding water, at low rate to keep the structure in equilibrium, or by an internal temperature jump caused by plasmonic heating of embedded gold nanorods (diameter 15 nm and length 60 nm; c = 9 nanorods/μm³) with laser light as mentioned above (see Figure S1). The gold skin contributes an additional heating effect. In the case of a temperature jump, the deformation follows a nonequilibrium transition path. The microgel can be considered as being prestressed and thus is capable of a rapid release of the elastic energy.

Figure 1 shows the geometrical parameter space describing the configurations generated by bending or buckling of a bilayer ribbon depending on its dimensions. Depending on the interplay of stretching and bending, the ribbons adopt a distorted equilibrium configuration that breaks the planar symmetry. For a given material composition, the stretching energy, accounting for in-plane deformations, is linear in the ribbon thickness h while the bending energy is cubic in h.¹⁹ These dependences entail that bending is more favorable for thinner films and for large h/w values ribbons coil up like a spiral spring. Wide and thin sheets adopt a cylindrical configuration. Coiling of ribbons with an intermediate h/w ratio is directed by the interplay of the two bending modes, resulting in a pronounced nonzero Gaussian curvature. A small gold-coated rectangular sheet will acquire a dome-like (elliptic) natural curvature upon swelling or deswelling of the hydrogel layer. For longer ribbons the principle curvatures become more unequal and the ribbon bends along a preferred direction set by the misfit in strain, including edge effects.^20,21 It tends to adopt a helical configuration as wound around a cylinder. For a given ratio of L/w ratio, we observe a two-dimensional spiral, a cylindrical helix, and a cylindrical tube as the ribbon becomes thinner. The sense of the helix is determined by small mismatches between the main stress axis and the long axis of the stripe. These are caused by inhomogeneity in thickness, shape, or bulk structure.^22,23

Figure 1.

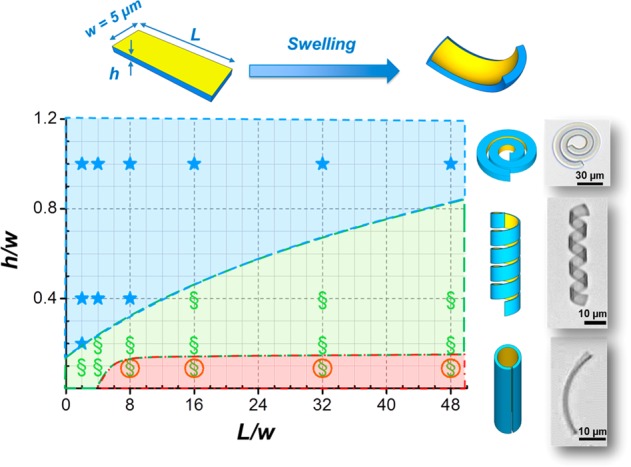
Shape diagram of bilayer ribbons with different cross sections and lengths and the corresponding schemes of minimum energy configurations. The length and the thickness are normalized to the constant ribbon width. Symbols mark the configurations found for ribbons coated with a 2 nm gold skin after swelling the poly(NIPAm) at ambient temperature in water. For details of the film preparation see ref (17).

Shape Changes during Equilibrium Heating

As mentioned already the poly(NIPAm) ribbon was prepared such that the gold layer was sputtered onto a planar ribbon. Upon swelling and shrinkage of the hydrogel layer, the construct bends in opposite directions below and above the volume phase transition temperature (Figure 2A). Indeed, a reversal of the curvature is observed upon heating/cooling, markedly at temperatures around the volume phase transition temperature. Figure 2B–D summarizes the observed temperature-dependent changes of the helical configuration of the bilayer ribbon under equilibrium conditions. At 20 °C, the ribbon shown in Figure 2B formed a tight right handed helix. As the temperature was raised, the helix widened and uncoiled until it approached the fully stretched state at about 31 °C. At higher temperatures a reversed helical conformation was formed that coiled up more strongly as the temperature was increased to 50 °C. Hence we observe a remarkable helix reversal as a function of temperature, that can be understood from the flat reference state of the gels, as defined by the preparative conditions,^17,24 in combination with the metallic skin that restricts isotropic swelling and shrinkage at low and high temperatures, respectively.

Figure 2.

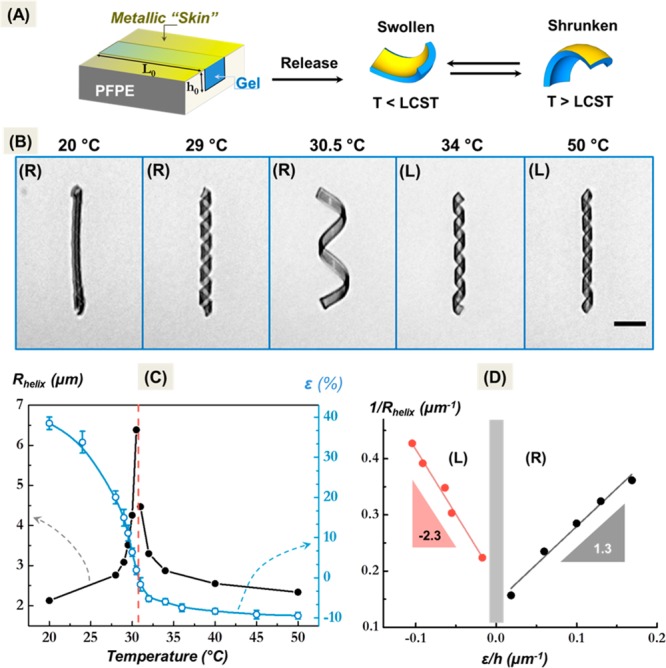
Helix reversal of a bilayer hydrogel ribbon around the volume phase transition. The volume change is constrained by a 2 nm thick metallic skin at one side. (A) Scheme of the fabrication and swelling/deswelling deformation of the microribbon. The ribbon was prepared in a mold of perfluorinated ether elastomer from a monomer solution in DMSO by photopolymerization.¹⁷ Still in the mold a 2 nm gold layer was sputtered on top of the hydrogel. When the hydrogel ribbons are suspended, swelling causes convex buckling controlled by the temperature respectively the solvent quality. (B) Optical micrographs of the coiled ribbon. At low temperatures a tight helix is formed. Upon deswelling of the hydrogel layer the helix undergoes an inversion in handedness (scale bar: 15 μm). (C) Variation of the helix radius with temperature (full symbols), and expansion in length (L – L₀)/L₀ of an unconstrained (without metallic skin) microribbon (open symbols). (D) Curvature (R and L) versus misfit strain relative to the ribbon thickness.

Figure 2C depicts uncoiling and coiling of the helix as measured by its radius as a function of the temperature and under equilibrium conditions. As the helix unwinds upon raising the temperature from 20 to 30.5 °C its radius R increases. When the temperature is raised further, the helix coils up in the reversed sense; the radius decreases again approaching asymptotically the configuration of the collapsed hydrogel layer. For comparison we plot the relative change in length ε for an unconstrained hydrogel ribbon (no metallic skin) of the same dimensions (see SI, Figure S4). The “skinless” ribbon continuously shrinks with temperature.

The steep change of the helix radius within a narrow temperature range, less than 1 °C is striking. The high sensitivity of shape and diameter, respectively, results in a well-developed singularity. This shows up clearly in Figure 2D, where 1/R is plotted versus the ε/h, with ε denoting the relative change in length of the free hydrogel (open symbols in Figure 2C). This behavior is similar to Timoshenko’s bending of a bimetallic strip. In that case the curvature is proportional to the misfit in strain of the two layers and inversely proportional to the thickness of the strip.¹⁹ Here we take the equilibrium expansion of the unconstrained hydrogel ribbon as an approximation for the misfit in strain between top and bottom side of the bilayer ribbon.

Figure 2D indicates that the experimental data follow a linear relationship rather well. The alteration of the slope of the 1/R versus ε/h relation at the helix inversion transition is in agreement with the change in bending modulus and thickness of the ribbon at the volume phase transition. Hence, although the volume phase transition of the nonionic hydrogel is continuous, it is sufficiently steep to cause an even more sharp transition in the bending behavior.

Dynamics

The transformation described so far occurs at slow temperature changes and thus under conditions where the system can follow the equilibrium transition. However, the plasmonic heating allows a jump-wise change of temperature that is in first instance localized to the volume of the hydrogel. This temperature change can be effected within microseconds, which is short with regard to both the diffusion time for swelling and deswelling and the time for elastic bending of the ribbon. The latter is controlled by polymer relaxation and the retardation due to the viscous drag exerted on the moving ribbon.²⁵ In the following we shall discuss this dynamic behavior.

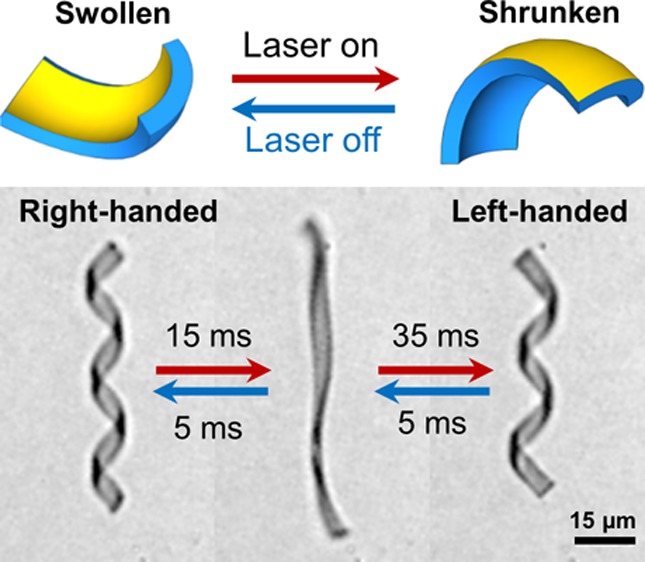
Figure 3 demonstrates the helix uncoiling and reversal as observed by light induced heating. The temperature of the water was externally regulated at 20 °C, significantly below the volume phase transition temperature of poly(NIPAM). The optical power has been set to cause the helical ribbon to fully unwind and reverse its chirality. The results depicted in Figure 3 demonstrate that uncoiling and reversal of the helix can be achieved within 90 ms (Figure 3A and B right panel). This time is still long compared to the thermal diffusion time but remarkably short for this complex motion. An even faster response is observed when the irradiation is ceased and the ribbon cooled down by the surrounding bath. A minimum of only 12 ms is needed to fully recover the initial helical state. Hence the off-time needed to recuperate the initial state (Figure 3B, right panel) is nearly an order of magnitude shorter than the on-time of the reversal process (Figure 3B, left panel).

Figure 3.

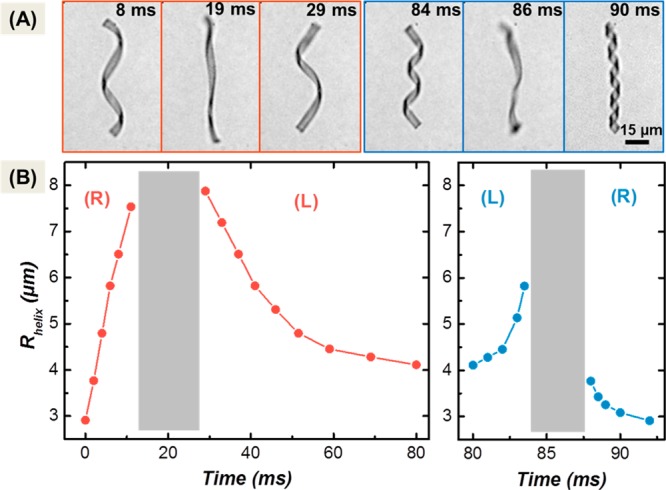
(A) Optical micrographs of the helical microgel in one cycle of actuation (80 ms on and 12 ms off). Laser irradiation starts at t = 0. Scale bar: 15 μm. (B) Radius of a right-handed helix (R) as a function of the irradiation duration. Left panel: recovery upon cooling after a light pulse of 80 ms. Irradiation was performed at 808 nm at an intensity of 1.7 W/mm² (see SI). The light intensity was enough to revert the chiral structure within 30 ms. The extra irradiation time (50 ms) effected recoiling to a left-handed (L) helix. The recovery process upon cooling takes place in a time interval of one tenth compared to the irradiation-driven helix inversion.

Let us consider the deformation to be a diffusion limited process. Then the rates for the uncoiling–coiling deformation should be related to the collective diffusion coefficient D_p of the water in the gel and to a diffusion length Δh. The latter corresponds to the shortest path for the water molecules to get out or into the gel, i.e., the height of the ribbon which is it smallest dimension. With D_p ∼ 2 × 10^–11 m²/s, the minimum time for swelling/shrinking of a 1 μm thick ribbon by 40% (corresponding to the volume change upon coiling or uncoiling, see Figure 2C) would require τ_p = 8 ms.^26,27 This value is close to the time needed to fully rewind the helix during cooling and fully unwind it during irradiation. The rewinding of the helix after inversion during irradiation, i.e., above the volume phase transition, required a longer time of about 50 ms. This retardation effect indicates that the diffusion of water out of the gel above the collapse temperature is probably significantly hindered, e.g., by the decrease of the diffusion coefficient as the gel collapses inhomogeneously starting from the surface. Such a skin effect is not expected upon reswelling. Even at high temperatures, dehydration is only partial, and the polymer volume fraction does not exceed 80%. Yet unwinding the helix upon cooling takes only 5 ms, a shorter time than estimated from diffusion. The observations indicate that the process does not follow the equilibrium swelling/deswelling trajectory. Nonequilibrium dynamics are also seen when we consider the changes near to the helix inversion point. According to the equilibrium trajectory in Figure 2C, most of the change in the radius of the helix takes place within an expansion/contraction interval of maximum 10%. Within this interval the response should be even faster, in the range of 1 ms. However, the helix reversal took 5 ms upon cooling and more than 10 ms upon heating/irradiation. Most probably the drag force acting on the moving ribbon could retard the large amplitude motion within this range.

In order to check the nonequilibrium deformation path we plot in Figure 4 the variation in the helix length against its radius for the slow helix reversal transition from Figure 2 and for the fast helix reversal effected by irradiation with laser light. Observation of the two geometrical parameters, length L and radius R, allows to record differences deformation mode of the ribbon during the transformation. Figure 4 depicts a huge difference of the trajectories for the equilibrium transformation and the light-induced transformation. While the former follows the same trajectory upon heating as upon cooling, the transformation effected by the light pulse depends strongly on the time parameters of the experiment. Obviously, these differences in the mechanical response are related to the ribbon deforming under nonequilibrium conditions. When the ribbon is not in its equilibrium state, it is prestressed and as such altered in its mechanical properties. During the deformation cycle the prestress changes dynamically. By varying the heating cooling cycle (irradiation and bath temperature) the trajectories upon heating and cooling can be manipulated widely, and the dynamic nonequilibrium can be optimized for maximum deformation. The response will, however, also depend on the gel properties. Variation of the swelling/deswelling properties of the gel, e.g., by ionic strength of the medium, by pH, or by binding of an analyte, will certainly alter the response characteristics.

Figure 4.

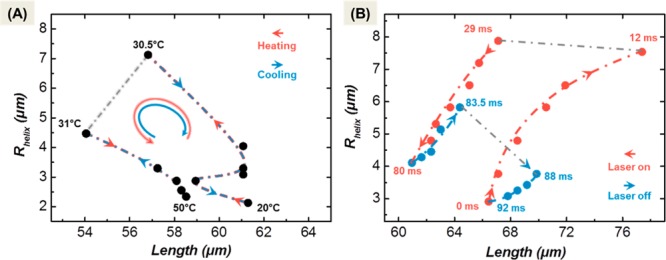
Plots of radius R versus length L for the bilayer ribbon during helix reversal. Panel A shows the deformation cycle under equilibrium conditions. Panel B depicts the deformation cycle for the same bilayer ribbon for the helix inversion cycle under nonequilibrium plasmonic heating (80 ms heating interval followed by a 12 ms cooling period). The huge difference in the geometrical trajectory demonstrates the effect of the prestressed state of the ribbon when it is not in its equilibrium configuration.

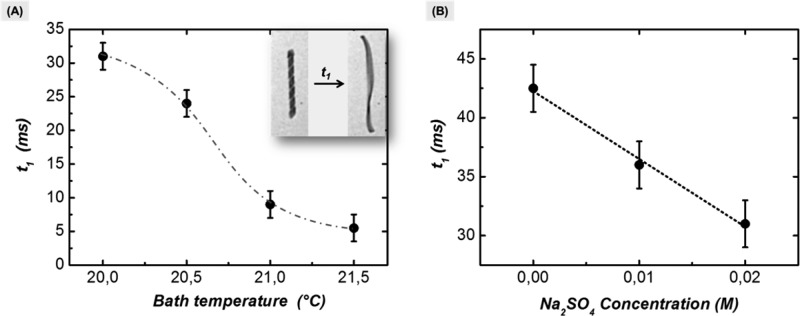
Figure 5 provides preliminary measurements for detecting small changes in bath temperature and upon the addition of salt. We monitored the variation of the helix diameter and length by recording the plots as shown in Figure 4 in response to irradiation with a fixed intensity. We quantify the sensor property by measuring the helix extension time during irradiation denoted by t₁ (see insert Figure 5A). This parameter can be determined rather reliably, and it is sensitive to the variations in the temperature of the bath and its salt concentration. Indeed, the nonlinear dependence of t₁ on the bath temperature indicates a sensitivity range of one tenth of degree. What is remarkable is the salt sensitivity of the extension time t₁ which is in the millimolar range. Also in this case the sensitivity exceeds that of other experiments, e.g., scattering techniques.²⁸ Further sensitivity improvements are foreseen through parametric optimization of the actuation. To use these helical ribbons as selective, the chemical sensor would requires tethering “receptors” to the helices by chemical or physical activation of their surfaces.

Figure 5.

Time required for unwinding of the helix for a given irradiation time depending on the bath temperature (A) and depending on the sodium sulfate concentration (B). The irradiation frequency was on/off 120 ms/30 ms. A detailed description of the measurement can be found in the Supporting Information (see Figure S7).

In conclusion, we demonstrated experimentally equilibrium and nonequilibrium actuation of confined swelling of a flat bilayer microgel. The comparison demonstrates a high actuation mode sensitivity of the volume change of microscopic hydrogels and its transformation to bending modes. By the plasmonic heating of microgels from inside, we have set up a system that enables well reproducible deviation from the equilibrium transition path. This allows us to control the spatiotemporal transformation under nonequilibrium conditions rather precisely and widely. An important aspect is that this is a cyclic process which can be repeated without changing the response of the hydrogel object as long as it is not degraded by aging. Here we demonstrated it at the example of a helix forming ribbon. Although the helix inversion by itself is an intriguing observation, it shows most importantly that the complexity of the interplay of the different deformations can be mastered rather accurately. Moreover, it demonstrates the transformation of a small amplitude swelling/deswelling to a large amplitude bending. By photothermal heating response times could be reduced to the millisecond range. The observed response did not only depend on the actuation/irradiation mode but also on the environment of the microscopic hydrogel. Thus, actuation and response was shown to be sensitive to small variations of the temperature and the composition of the aqueous sol, in which the gel was immersed. This sensitivity is most pronounced near to the volume phase transition and may be useful to detect specific analytes that bind either to the surface of the gold layer or within the gel or modify the interaction of the water with the gel. The principle of nonequilibrium morphing implies that the systems dissipate energy but may also perform work. This can be transferred to hydrogel objects with other, more elaborated geometries and response modes.²⁹ These new possibilities of morphing three-dimensional microgels with fast dynamics may find applications in fields such as soft-robotics, microfluidics, and artificial microswimmers.^30,31

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.nanolett.7b00015.

• Brief description of the s and modification of gold nanorods (AuNRs); preparation of the gold nanorods loaded microgels; microscopy observation of helical microgel at different temperatures; photothermal heating and optical microscopy monitoring of the actuation; effects of salt and temperature on the deformation kinematics (PDF)

• Video S1. Slow motion video of a microgel helix undergoing handedness inversion under one irradiation period with an on/off time of 80 ms/12 ms. The video frame rate is 20 fps which correspond to a slowdown factor of 100 (AVI)

• Video S2. Slow motion video of helical microgel at different bath temperatures undergoing inversion under one irradiation cycle. On the left movies the water temperature was 20 °C, while on the right one it was 21.5 °C. The irradiation period was 120 ms/30 ms (on/off). The video frame rate is 50 fps which correspond to a slowdown factor of 40 (AVI)

• Video S3. Slow motion video of a helical microgel under one irradiation cycle at different salt concentrations (0.0 M on the left and 0.02 M on the right). The irradiation has an on/off period of 120 ms/30 ms. The video frame rate is 50 fps which correspond to a slowdown factor of 40 (AVI)

The authors declare no competing financial interest.