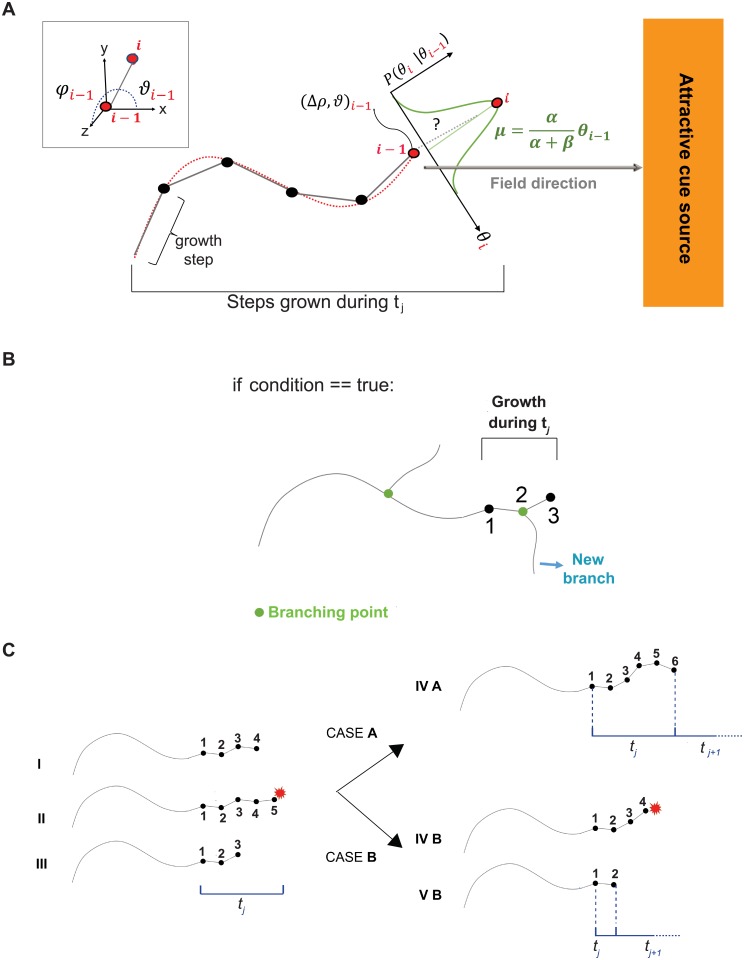
Fig 1. 3D mathematical model of individual axon growth.

(A) The axon elongates step by step (grey segments), each step being delimited by the current point in space i and the previous one, i − 1. Each i^th new step is described by its spherical coordinates (Δρ, ϑ, φ) (represented in 2D for simplicity; see upper left corner for a 3D view), and placed after the previous position i − 1. The exact position of the i^th point is defined (in 2D) by ${\theta }_{xy}^i=f\left({\varphi }_{x,y}^i\right)$, which is drawn from a conditional Normal probability distribution (in green). The most probable value (mean of the distribution (μ)) considers the directions of the last step i − 1 and of the attractive field, each contribution weighted by α and β respectively. For each time unit t_j, a maximum number of steps (n_max) is allowed. (B) Algorithmic implementation of branch generation. During t_j, a certain number of growth steps are performed (3 in this schematic representation). At the end of t_j, a certain “condition” is evaluated and, if true, a branch point is placed at the axon tip, or at any other step performed during t_j (step 2). (C) Step by step axon growth scheme during t_j considering physical interactions. The axon elongates of n steps (I), until it encounters a mechanical constraint (II) and retracts (III). During the same time interval t_j, it will re-try to reach n_max steps (6 in this example). If no other mechanical constraint is encountered (CASE A), the axon will advance to reach n_max steps. If, on the contrary, another mechanical constraint is encountered (CASE B), the axon will retract again and stop its growth until the next time point (t_j+1). In this case, the total growth during t_j is then smaller than n_max steps.