Fig. 5.

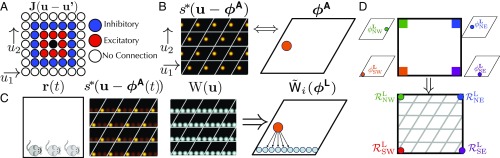
(A) A 2D neural sheet with short-range excitation and long-range inhibition, analogous to Fig. 1. Each neuron on the continuous sheet now has coordinates $\mathbf{u}=\left(u_1,u_2\right)$. (B) A 2D analogue of a single attractor pattern on the neural sheet, with high firing rates in red (compare with Fig. 1). The set of all unique stable attractor patterns is now indexed not by a single phase variable as in 1D, but by a 2D phase variable ${\mathit{\varphi }}^{\mathbf{\text{A}}}$ ranging over a rhombus or unit cell. Copies of the unit cell are shown via white lines. (C) The landmark cell Hebbian weights will be a combination of 2D attractor states (Eq. 13). As the animal travels along the south wall, the average firing rates will form a “streak” across the neural sheet. This leads the Hebbian weights on the neural sheet to form the same streak; this learned state can be represented as a distribution over the periodic rhombus. Analogously, there is a force law, where the state of an attractor network ${\mathit{\varphi }}^{\mathbf{\text{A}}}$ will be pulled toward this distribution ${\tilde{\text{W}}}_i\left({\mathit{\varphi }}^{\mathbf{\text{L}}}\right)$ (Eq. 15). (D) Similar to Fig. 4D, we can unroll the 2D attractor phase into a 2D position variable, thereby associating landmark pinning phases to points in physical space. Given landmarks in all four corners, the landmark pinning phases correspond to different points on the phase rhombus, but through unrolling this rhombus, each one can be associated to a physical corner of the environment.