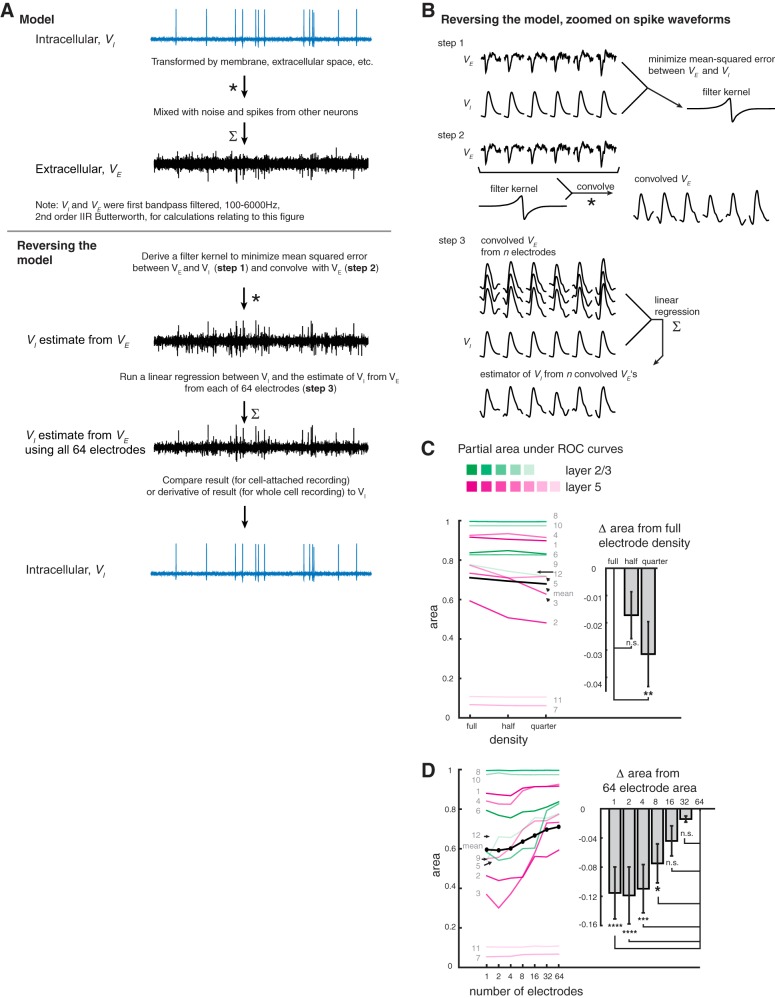
Fig. 5.
An algorithm for assessing potential spike sorting performance as a function of electrode density and quantity. A, top: a model in which the intracellular voltage (VI) is transformed by membrane capacitance and resistance, conductance delays, etc., and mixed with noise and spikes from other neurons to produce an extracellular voltage (VE) as sensed on an electrode. Bottom: reversal of the model in A, in which the VE is transformed to better resemble the VI and is unmixed from noise and spikes of other neurons to better approximate VI. Unmixing is performed by linearly regressing the transformed VE against the VI. B: details of the inverted model, zoomed on individual spike waveforms. Top: step 1, a transformation that minimizes the mean squared error between the VE from a single electrode (we will consider each individual electrode in turn) and calculates VI, yielding a filter kernel (shown are 6 spikes from an actual recording for ease of visualization.) Middle: step 2, the VE from the same electrode used in step 1 is convolved with its corresponding convolution filter kernel to create the “convolved VE.” Bottom: step 3, electrodes are ordered by amplitude, as described for Fig. 2C, and the electrodes to be included in the analysis [i.e., 64, 32, or 16 electrodes (full, half, and quarter density, respectively) for C or the first N electrodes for D) are chosen. Steps 1 (top) and 2 (middle) are applied to the voltage of each of these chosen electrodes, and a multiple linear regression is performed between these convolved VEs and the bandpass-filtered patch voltage. The resulting regression coefficients are multiplied by their respective convolved VEs and summed, yielding a single estimator of patch voltage from VEs (step 3, bottom). C: partial areas under the curve (PAUC) for partial receiver operating characteristic s (PROCs) from each neuron, as in Fig. 4A, but thresholding on the derivative of the estimator of patch voltage. Inset: comparison of scenarios when the estimator of patch voltage was generated from the top 64 amplitude-ordered electrodes in a recording as a full set (full density), when every 2nd electrode was skipped (i.e., the 1st, 3rd, 5th, etc., electrodes were included for a total of 32 electrodes; half density), or when 4 electrodes at a time were skipped (i.e., the 1st, 5th, 9th, etc., electrodes were included for a total of 16 electrodes; quarter density). These results and the results in D were generated when all spikes of the patched neuron were included (i.e., not excluding burst spikes). A significant effect of electrode density was observed (repeated-measures one-way ANOVA, F = 5.656, P = 0.0104, n = 12 neurons from 7 mice). The mean PAUC of the full-density group was significantly greater from that of the quarter-density group (mean of full-density area minus mean of quarter-density area, or “mean difference” was 0.03148; Dunnett’s multiple comparisons test, with corrected **P = 0.0054), but not that of the half-density group [mean difference = 0.01722, P = 0.1401, n.s. (not significant, P > 0.05)]. D, left: PAUC values derived from the derivative of the estimator of patch voltage generated from the top N amplitude-ordered electrodes in a recording (individual neurons colored as in C, mean in black). Inset: PAUC differences from the 64-electrode group (light gray, with error bars representing SE of the difference). A significant effect of number of electrodes was observed (repeated-measures one-way ANOVA, F = 8.364, P < 0.0001, n = 12 neurons from 7 mice). The mean PAUC for 64 electrodes was compared with that for N = 32, 16, 8, 4, 2, and 1 electrode(s). The mean differences from subtracting the 2 values, and the P values, are as follows: 0.01407 and 0.9817 (N = 32 electrodes; n.s.), 0.04402 and 0.28332 (N = 16; n.s.), 0.07483 and 0.0149 (N = 8; *P 0.01–0.05), 0.1095 and 0.0002 (N = 4; ***P = 0.0001–0.001), 0.1187 and 0.0001 (N = 2; ****P ≤ 0.0001), and 0.1153 and 0.0001 (N = 1; ****P ≤ 0.001; Dunnett’s multiple comparisons test).