Figure 4.

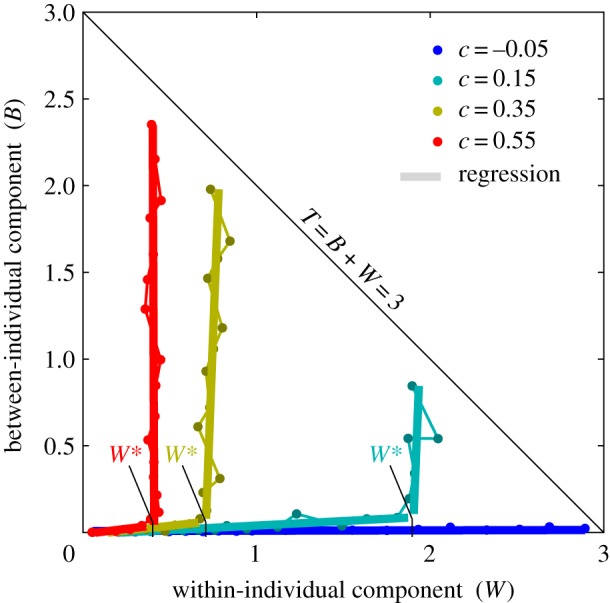
Our numerical results on niche evolution show that niche expansion follows either of two orthogonal principles determined by the cost of individual generalization c and resource diversity σ_K. For c < 0, populations inevitably achieve niche expansion by parallel release. For c > 0, populations switch between parallel release and strict phenotypic differentiation at a critical within-individual niche width W*. At low resource diversity, resulting in low total niche width T, populations achieve niche expansion by parallel release, and at high resource diversity populations achieve niche expansion by strict phenotypic differentiation. The point of switching, at the critical within-individual niche width W*, decreases with the cost of individual generalization c. Points represent simulation results for ${\sigma }_{\mathrm{K}}^2$ ranging from 0.05 to 3.0 for each uniquely coloured cost-level. Corresponding (thick) regression lines were produced by piecewise major axis regression (choosing the maximum-likelihood switch point). Here, we used q = b = 1, m = 0.1, r = 100 and K₀ = 2 (see Material and methods).