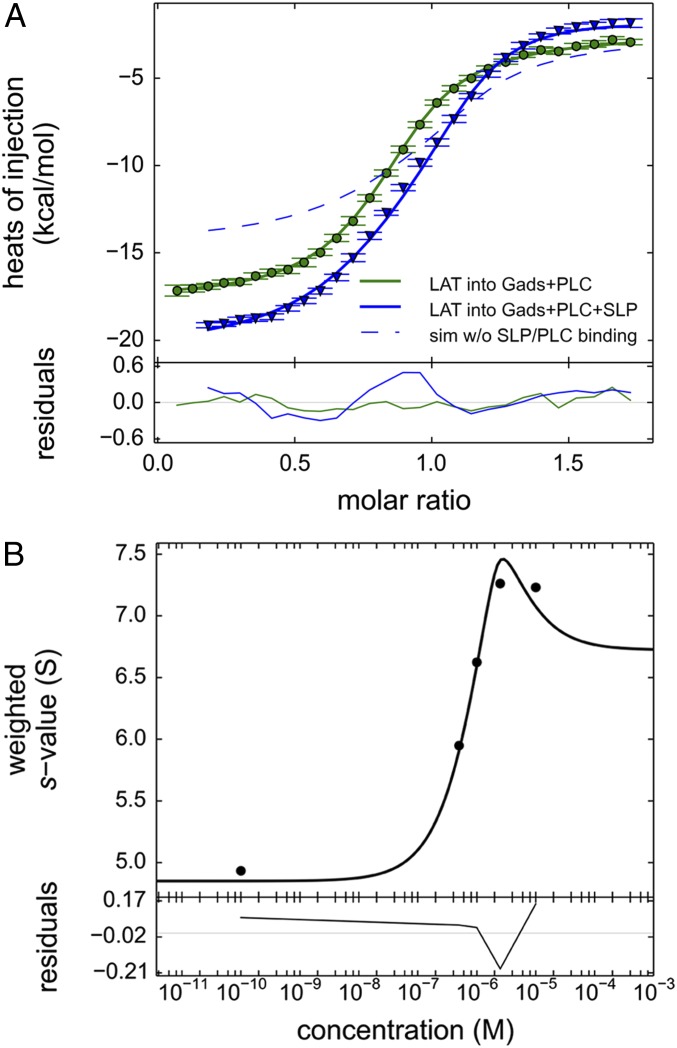
Fig. 5.
Comparison of ITC binding isotherms titrating pLAT to form ternary and quaternary complexes. (A) pLAT at 50 μM in the syringe was injected into an equimolar 5-μM mixture of Halo-GadsFL and PLC-γ1FL (green circles), which allows the formation of a ternary complex, or into an equimolar 5-μM mixture of SLP-76tr, Halo-GadsFL, and PLC-γ1FL (blue triangles) allowing the formation of a quaternary complex. The data were fitted to a binding model with three or four coupled equilibria, respectively (solid lines), as described in detail in SI Appendix, Supplementary Methods and schematics in SI Appendix, Fig. S1. The model for the ternary mixture (green line) was constrained to the ΔH and ΔS values for the binary interfaces determined in separate experiments (Table 1), refining the estimates ΔΔH and ΔΔS for the enthalpic and entropic contributions from cooperativity in the Halo-GadsFL/pLAT/PLC-γ1FL ternary complex (Table 2). The cooperativity parameters of the ternary complex, in turn, were fixed in the model for the quaternary mixture (blue line), now additionally including equilibrium populations of the quaternary complex SLP-76tr/Halo-GadsFL/pLAT/PLC-γ1FL, from which best-fit parameters for ΔΔHquad and ΔΔSquad as well as the total heat change and entropy change of the quaternary complex ΔHquad and ΔSquad were determined. For comparison, the theoretically expected titration curve for ΔΔHquad = 0 and ΔΔSquad = 0, i.e., in the absence of any SLP-76tr interactions other than those observed in binary complexes with GADS and ternary complexes with GADS and pLAT, is shown as a dashed blue line. (B) Weighted-average c(s) of mixtures of pLAT488, Halo-GadsFL, and SLP-76tr, each at 2.5 μM, as a function of PLC-γ1FL (black circles) and theoretical model of coupled equilibria (black line) based on binding and cooperativity constants predetermined by ITC.