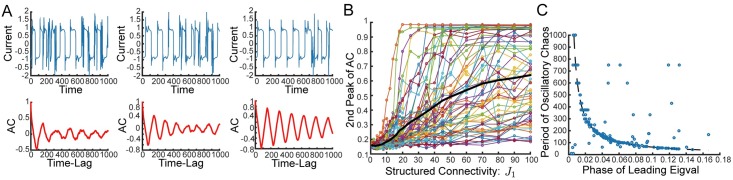
Fig 6. Realization-dependent oscillatory imprint on the self-tuned chaotic regime.

(A) Sample traces $\overline{h}\left(t\right)$ (top), and normalized autocorrelation $\overline{q}\left(\tau \right)$ (bottom) of coherent mode current for a connectivity realization with complex eigenvalue for J₁ = 25,30,35 increasing from left to right. Dynamics exhibit pronounced oscillatory power and the autocorrelation exhibits a pronounced peak near the same frequency that will dominate the limit cycle for larger J₁. (B) Height of second peak of the autocorrelation of the coherent mode input as a function of J₁. Each colored line represents a single connectivity realization, averaged over 10 initial conditions. For many realizations, there is a significant second peak in the autocorrelation over a long range of values of J₁ well before a limit cycle is reached. We display the 63 realizations which had complex leading eigenvalue out of 100 in this set of trials. Thick black line shows average over those realizations. (C) Observed period of oscillatory chaos vs phase of leading eigenvalue for 181 realizations from which we were able to measure an oscillatory period with chaotic fluctuations (out of 196 realizations with complex leading eigenvalue in this set of trials. In order to confine to realizations and values of J₁ that yielded chaos, we restrict to those with second peak of autocorrelation less than 0.8. These had average height of second peak over all realizations: 0.5). Dotted line shows prediction from theory: $\frac{2\pi }{\text{Phase}\left({\lambda }_1\right)}$. The bulk of realizations are very well predicted although a notable fraction are not. The median error of prediction was 7.75 (average period over these realizations: 231, std: 212). N = 8000 for all panels.