Accelerating QM/MM Free Energy Computations via Intramolecular Force Matching

Abstract

The calculation of free energy differences between levels of theory has numerous potential pitfalls. Chief amongst them is the lack of overlap, i.e., ensembles generated at one level of theory (e.g., “low”) not being good approximations of ensembles at the other (e.g., “high”). Numerous strategies have been devised to mitigate this issue. However, the most straight-forward approach is to ensure that the “low” level ensemble more closely resembles that of the “high”. Ideally, this is done without increasing computational cost. Herein, we demonstrate that by reparameterizing classical intramolecular potentials to reproduce high level forces (i.e., force matching) configurational overlap between a “low” (i.e., classical) and “high” (i.e., quantum) level can be significantly improved. This procedure is validated on two test cases and results in vastly improved convergence of free energy simulations.

1. Introduction

Obtaining highly accurate free energy differences via molecular simulations remains an open challenge. So-called alchemical free energy simulations (FES) are rapidly becoming a standard tool in computational chemistry.^1–5 While most FES employ molecular mechanical (MM) force fields, the use of hybrid quantum chemical / molecular mechanical (QM/MM) Hamiltonians may be required. ^6–11 Using high level QM methods is, in principle, straightforward and permits a much more accurate representation of inter- and intra-molecular interactions. However, to compute free energy differences accurately necessitates adequately sampling the configurational space of interest.^12,13 For the foreseeable future performing the associated configurational sampling with high level QM/MM methods remains prohibitively expensive.

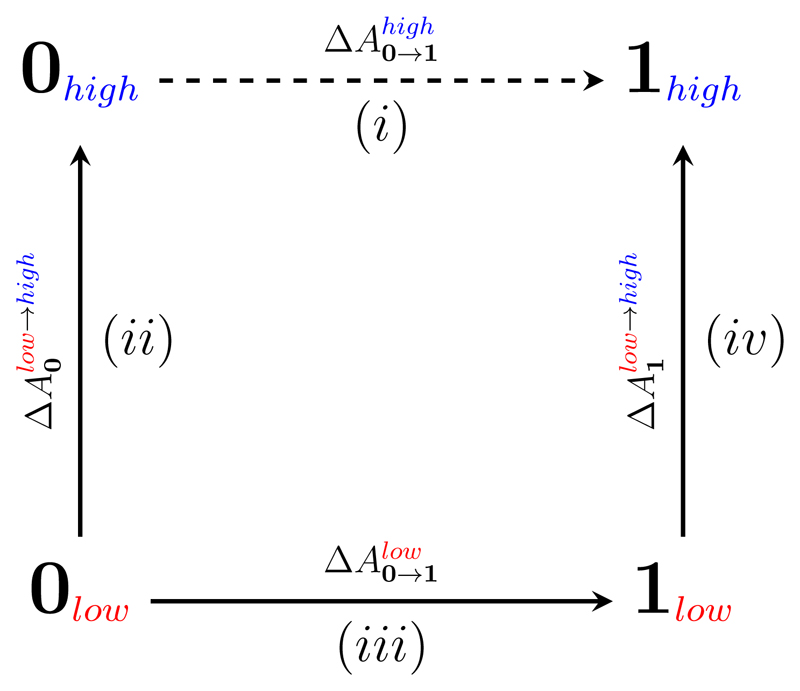
To circumvent this obstacle, the “indirect” approach to FES is widely utilized (Fig. 1).^14–19 In this approach, the quantity of interest $\text{Δ}{A}_{\mathbf{0}\to \mathbf{1}}^{high}$ (dashed arrow, step (i) in Fig. 1) is computed via steps (ii)-(iv). In step (iii) the free energy $\text{Δ}{A}_{\mathbf{0}\to \mathbf{1}}^{low}$ between the two states is computed at a low level theory, using any standard method of choice (BAR, MBAR, vFEP, WHAM, etc.)^20–23 Steps (ii) and (iv) “correct” the free energies of each end state by accounting for the free energy difference between levels of theory. In most applications of the indirect cycle approach, the free energy differences ΔA^low→high were obtained by “one-sided” free energy perturbation, often referred to as Zwanzig's equation (FEP, Eq. 1).²⁴

$$\text{Δ}{A}^{low\to high}=-\frac{1}{\beta }\log {\langle \exp (-\beta \text{Δ}{U}^{low\to high})\rangle }_{low}$$ (1)

One can clearly see the advantage of using FEP, as the ensemble average of interest (〈…〉_low) is generated at the low level of theory (i.e., simulations only need to be run at the low level of theory).

Figure 1.

The thermodynamic cycle of the indirect FES scheme

However, recent work has shown that convergence issues, due to insufficient configurational overlap between levels of theory, are almost unavoidable when using FEP.^25,26 Failure of Eq. 1 to converge has largely been attributed to disparities between the intramolecular degrees of freedom (i.e., differences in bonds, angles, and dihedrals).^26–32 Much of our previous work has focused on utilizing better approaches in computing ΔA^low→high with significant success. ²⁸,³¹,³³,³⁴ The use of non-equilibrium approaches, specifically Jarzynskis non-equilibrium work theorem, has proven particularly helpful.^33,34

$$\text{Δ}{A}^{low\to high}=-\frac{1}{\beta }\log {\langle \mathcal{exp}(-\beta W^{low\to high})\rangle }_{low}$$ (2)

Eq. 2, introduced by Jarzynski in 1997,³⁵ operates in a similar capacity to FEP (Eq. 1), but instead of potential energy differences, we now use values obtained from fast-switching non-equilibrium work simulations.

When using Eq. 1 to connect levels of theory,^33,34 the length of the switching simulations required to generate converged ΔA^low→high depended largely on the magnitude of configurational mismatch between the levels of theory (e.g., between 50 fs to 5 ps depending on severity). In other words, if the disparity between low and high level configurations is (too) large, the computational cost to converge the free energy difference quickly increases. This suggests that in addition to utilizing more robust methods to compute free energy differences ΔA^low→high accurately, it may be necessary to modify the chosen low level of theory in a manner that ameliorates configurational disparity. In fact, if the configurational mismatch between the two levels of theory were sufficiently small, it should be possible to compute the free energy differences (ii) and (iv) of Fig. 1 with just FEP. The obvious choice for an improved low level of theory would be the use of more rigorous methods (e.g., semi-empirical quantum mechanics (SQM) instead of molecular mechanics (MM)). However, the only real requirement for a better low level of theory is that configurational overlap is improved relative to the target, high level, Hamiltonian.³⁶ Hence, we aim to improve the convergence of ΔA^low→high while retaining the efficiency of a classical force field.

There have been countless efforts towards improving low level force fields to better reproduce QM energetics and configurations (e.g., to name a few, corrections to protein backbone dihedrals, and incorporation of polarizability^37–39), with varying degrees of success through many forms of validation. However, often times the implicit need for parameter transferability, as well as the approach to parametrization in popular force fields can inhibit configurational overlap with desired QM levels of theory. To be more specific, in the case of the CHARMM⁴⁰ General Force Field⁴¹ (CGenFF), molecules are parameterized to reproduce MP2/6-31G* energetics in condensed phase. It stands to reason that these same parameters would perform poorly when applied to a system in gas-phase, and/or attempting to produce an ensemble of DFT-like configurations. This is evidenced by work from Mackerell et al. to improve the description of peptide backbones in the CHARMM22 force field with grid based corrections.⁴² After applying the so-called “CMAP” correction, they found that the agreement with respect to condensed phase QM properties was improved, but gas phase performance deteriorated. They concluded that “it is evident that the current potential energy functions in use cannot simultaneously treat both gas and condensed phases with high accuracy”.⁴²

Herein, we explore an approach that forgoes transferability and reparameterize the low level force fields for the system of interest on a “case by case” basis. In the interest of our goal (i.e., increasing configurational overlap with the high level Hamiltonian), we seek to find a parameter set that best reproduces the high level forces and, therefore, the generated configurational ensemble. This approach is commonly referred to as force matching (FM),^43,44 and has been used in the past to adjust potential forms ranging from coarse-grained⁴⁵ (CG) to semi-empirical quantum^46–48 (SQM). In essence, the fitting is performed by taking a collection of generated configurations (i.e., a test set) and computing high level forces (e.g., SQM or QM) for each configuration. Parameters from the potential of interest (e.g., SQM, MM, or CG) are then adjusted until the difference between the high level force and the estimated force is minimized. Although in some cases the configurations were generated via high level (e.g., ab initio QM) dynamics, this need not be the case. Often referred to as either “on the fly” or “adaptive FM”,^49–57 initial configurations are generated using standard force field parameters, which are then fit to create a set of force matched parameters. The resulting parameters are then used to generate more configurations, which are again fit. This process is repeated until satisfactory convergence is achieved. In fact, the work performed in Ref. 53 strongly demonstrates the ability of adaptive force matching to improve the quality of ensembles generated by reweighing force matched configurations to evaluate QM ensemble averages, with strong implications for its use with the FEP equation.

When attempting to make the low level “more similar” to the desired high level of theory, the question arises how to describe / quantify “similarity”. As observed, e.g., by Bennett, to compute a converged free energy difference between two states of interest, it is a fundamental criterion that there is overlap between the potential energy difference distributions.²³ More specifically, in the context of computing ΔA^low→high, this requires that the distribution of potential energy differences from the low level ensemble, P_low (ΔU^low→high), and from the high level ensemble, P_high(‒ΔU^high→low), overlap (i.e., P_low(ΔU^low→high) ∩ P_high(‒ΔU^high→low) ≠ 0, see Fig. S3a). Overlap of these probability distributions indicates how well configurations sampled at the low level of theory represent important (e.g., low energy) regions of the high level conformational space.⁵⁸ If the overlap is non-existent, no equilibrium approach will succeed, and use of non-equilibrium techniques is advised.

When using two-sided approaches, such as Bennett’s acceptance ratio (BAR), a relatively small degree of overlap suffices to obtain converged results. However, this would require generating ensembles at the low and high levels of theory, which in many applications is not practical. To achieve convergence using one-sided methods (e.g., FEP), at least some configurations sampled (e.g., the low level of theory in our application) must also be relevant at the respective other end point (the high level of theory in our case).^58,59 In other words, a much higher degree of overlap is required when using FEP compared to BAR. These considerations also hold true for use of non-equilibrium approaches (e.g., JAR and the two sided Crook's equation, CRO⁶⁰). Here insufficient overlap in the relevant work distributions, P_low(W^low→high) and P_high(‒W^high→low), can, in principle, be mitigated by increasing switching simulation lengths, but the computational expense may render this impractical.

As mentioned earlier, the difficulty of converging free energy differences between levels of theory with one-sided approaches (e.g., FEP) was attributed to discrepancies in the intramolecular degrees of freedom between high and low level configurational space. While the differences in the “stiff” (e.g., bonds and angles) intramolecular degrees of freedom between levels of theory is often considered the prohibitive factor⁹,³⁰,^32–34,^61–67 to computing ΔA^low→high, the discrepancy can be ameliorated rather quickly using non-equilibrium work (i.e., JAR) approaches. In the case of computing the QM torsional PMF of gas phase butane, we achieved converged ΔA^MM→QM results with as little as 1000 switches of 50 fs length.³³ The real challenge proved to be the conformational disparity resulting from the “soft” intramolecular degrees of freedom (e.g., dihedral conformational preferences), as was the case for computing ΔA^MM→SQM for gas phase “blocked” serine dipeptide (i.e., N-acetylmethylamide serine, Ser), specifically the backbone ϕ,ψ dihedral angles and the χ₁ sidechain dihedral angle (Fig. S1).³⁴ This suggests that to investigate the utility of FM to help improve convergence when calculating the correction steps (ii) and (iv) in indirect cycle QM/MM FES simulations, one should initially focus on the intramolecular degrees of freedom, both the “stiff”, as well as the “soft” ones. Therefore, in this study we apply FM to modify the bonded energy terms of typical MM force fields.

Methods

As mentioned, to reduce computational cost in practice one has to compute ΔA^low→high (the correction steps (ii)/(iv) of Fig. 1) by one-sided methods (FEP, JAR). Having just outlined why converging such calculations is difficult, they are complicated further by the fact that the convergence of the resulting free energy differences is difficult to assess. Since no ensembles are generated at the high level of theory, information about the overlap between forward and backward distributions (as depicted in Fig. S3a) is not available. Recently, Boresch and Woodcock³⁶ investigated this question and proposed two practical criteria. First, since in FEP and JAR the key step is averaging over exponentials 〈exp(–βX)〉, where X = ΔU^low→high for FEP and X = W^low→high for JAR, the associated standard deviation, σ_X (Fig. S3b) must not be too large.^68,69 Comparing results obtained with FEP and JAR to reference results obtained with two-sided methods (Bennett, Crooks theorem), they recommended that σ_X ≤ 4k_BT (~2.4 kcal/mol).

Second, they utilized the so-called bias measure Π_X of Wu and Kofke⁵⁹

$${\text{Π}}_X=\sqrt{{\mathbf{\text{W}}}_L\left[\frac{1}{2\pi }{(N-1)}^2\right]}-\sqrt{2\beta \left({\langle X\rangle }_{low}-\text{Δ}{A}^{low\to high}\right)},$$ (3)

where W_L is the Lambert function, ΔA^low→high is the result obtained with either FEP or JAR, and N is the sample size. In line with the recommendations of Ref. 59, Boresch and Woodcock found that FEP and JAR results agreed with reference results once Π_X > 0.5. While these two guidelines are at best necessary, rather than sufficient criteria for convergence, they certainly can detect cases where FEP, and possibly JAR results are likely to be unreliable. In this work, we will use them to describe how disparities between low and high levels of theory are reduced when attempting to improve the low level by FM.

The work performed focuses on computing free energy differences between a low and high level of theory for two gas-phase test cases: butane and “blocked” serine dipeptide. For both molecules, all simulations were performed using langevin dynamics (LD), at 300K with a friction coefficient of 5 ps⁻¹ and a 0.5 kcal/mol·Å² harmonic center of mass restraint. Details for the functional form of the intramolecular FM, as well as the training sets generation and a flow chart outlining the matching process are provided in Supporting information (SI Sec. 1 and SI Sec. 4, respectively).

Butane

The initial low and high levels of theory are, MM[CGenFF] and DFTB3 respectively, and MM[FM] as the resulting parameter set from the FM procedure.^† Ensembles for DFTB3 and the MM[FM] parameter set were generated under conditions identical to the MM[CGenFF] training set (see SI Sec 3.1), which was used in the overlap calculations seen in Fig. 2. To compute the butane PMFs, we generated 1 ns LD simulations with a 100 kcal/mol·rad⁻² harmonic restraint on the C-C-C-C dihedral angle centered at 10° increments between 0° and 180°, for a total of 19 simulations, at each aforementioned level of theory (MM and DFTB3). All dynamics were performed with a 1 fs time step and configurations were saved every 0.1 ps (i.e., 10,000 configurations per dihedral). The classical MM and reference DFTB3 PMFs of butane were generated using Multistate Bennett Acceptance Ratio (MBAR).²⁰ Following this, FEP was used to compute ΔA^MM→DFTB3 along each step of the MM reaction profile. Each FEP calculation was performed with 10,000 MM configurations (i.e., 10,000 DFTB3 single point energies), and was used to indirectly compute the DFTB3 PMF. Estimations of standard deviation and hysteresis were performed by dividing the 10,000 data points used in each FEP calculation into 10 sequential blocks of 1,000 configurations. From each block, FEP was performed and the distribution of these estimates yielded the variance (as outlined in Ref.33).

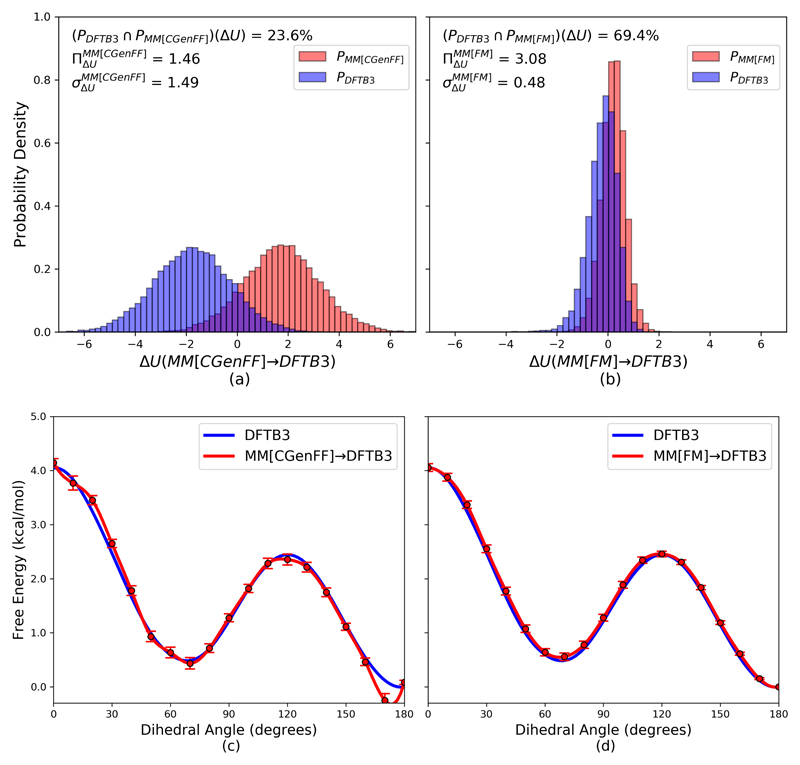
Figure 2.

(a) Gas-phase butane potential energy difference histograms between a high level DFTB3 (P_DFTB3 configurations) ensemble and a MM[CGenFF] (P_MM[CGenFF] configurations) low level ensemble. (b) Gas-phase butane potential energy difference histograms between a DFTB3 and a MM[FM] (P_MM[FM] configurations) low level ensemble. Histograms (P_DFTB3, P_MM[CGenFF], and P_MM[FM]) were generated using 20,000 configurational snapshots from a 2 ns LD simulation. (c) Comparison of the gas-phase butane dihedral potential of mean force (PMF) generated with FEP using MM[CGenFF] as the low level of theory (ΔA^{MM[CGenFF]→DFTB3}) using data from 1 ns of LD (10,000 points every 10°, red) to a reference DFTB3 PMF generated with MBAR (10,000 points every 10°, blue). (d) Comparison of the gas-phase butane dihedral potential of mean force (PMF) generated with FEP, but using using MM[FM] as the low level of theory (ΔA^{MM[FM]→DFTB3}) using data from 1 ns of LD (10,000 points every 10°, red) compared to the reference DFTB3 PMF (blue).

Serine

The initial low level of theory was MM[C22(CMAP)] and DFTB3 was used for the high level; our force matching procedure was used to derive MM[FM] as the alternative, low level of theory.^‡ Once the MM[FM] parameters were found, gas phase Ser LD simulations were carried out. These consisted of 10 LD simulations using both MM force fields, each starting from random initial velocities, a time step of 0.5 fs, and a production length of 100 ns (1 μs total production per force field). A 1 ns equilibration prefaced each simulation and coordinate/velocity sets were saved every 10 ps (100,000 total). Gas phase DFTB3 LD Ser simulations were performed with a 500 ps equilibration and production length of 10 ns for 10 random starting velocities (100 ns total). Each simulation had a time step of 0.5 fs and configurations/velocities were saved every 5 ps (20,000 total). The MM coordinate snapshots were used to compute P_MM (ΔU^MM→DFTB3) and DFTB3 coordinate snapshots were similarly used to compute P_DFTB3 (‒ΔU^DFTB3→MM) for both butane and Ser.

From the coordinate and velocity sets gathered for Ser, two sets of non-equilibrium switching simulations were performed, one set switching from MM to DFTB3 (i.e., the forward work direction) and the other switching from DFTB3 to MM (i.e., the backward work direction). This data was used to obtain P_MM (W^MM→DFTB3) from the forward switches, and P_DFTB3 (‒W^DFTB3→MM) from the backward switches. Non-equilibrium work values were generated with the MSCALE⁷³ facility in CHARMM via the PERT slow growth procedure, which when shifted rapidly is equivalent to non-equilibrium work (see Ref. 33, 34, 69 for more details). Each of the non-equilibrium switching simulations was initiated using coordinate/velocity information saved incrementally during MM and DFTB3 dynamics production phase (vide supra) and thus allowing for the calculation of overlap between work distributions.

Results and Discussion

Butane

We first tested our FM procedure by generating a MM[FM] ensemble for butane in the gas phase without restraints. From this, we computed the P_low(ΔU^low→high) and P_high(‒ΔU^high→low) overlap of our low (MM) and high (DFTB3) level ensembles (Fig. 2). Qualitatively, we see that the overlap with DFTB3 increased dramatically by using MM[FM] instead of MM[CGenFF]. In fact, the overlap of MM[FM] is nearly three times greater than that of MM[CGenFF] (69.4% vs. 23.6%, respectively). It is also worth noting that the standard deviation of ΔU for $\text{MM}[\text{FM}]({\sigma }_{\text{Δ}U}^{\text{MM}[\text{FM}]}=0.48\text{kcal}/\text{mol})$ is three-fold lower than for $\text{MM}[\text{CGenFF}]({\sigma }_{\text{Δ}U}^{\text{MM}[\text{CGenFF}]}=1.49\text{kcal}/\text{mol}).$ Further, the MM[FM] bias measure $({\text{Π}}_{\text{Δ}U}^{\text{MM}[\text{FM}]}=3.08)$ is twice that of MM[CGenFF] $({\text{Π}}_{\text{Δ}U}^{\text{MM}[\text{CGenFF}]}=1.46)$.

Using our newly generated MM[FM] parameters, we investigated the ability to reproduce butane's rotational PMF about its central bond at the DFTB3 level. Two low level PMFs (MM[CGenFF] and MM[FM]) were generated via MBAR, applying corrections from the low to high level of theory using FEP at each value of the dihedral coordinate (in generalization of the correction steps ii./iv. of Fig. 1). The resulting PMFs are shown in Fig. 2. Examining the indirect PMF generated with ΔA^{MM[CGenFF]→DFTB3}, we see rather marked deviations from the reference DFTB3 PMF $(\overline{RMSD}=0.12\text{kcal}/\text{mol})$ with a maximum deviation of 0.37 kcal/mol. This is largely in contrast with the PMF obtained using ΔA^{MM[FM]→DFTB3}, which has noticeably smaller error bars and a smaller deviation from the reference $(\overline{RMSD}=0.07\text{kcal}/\text{mol})$ with a maximum of only 0.13 kcal/mol.

Serine

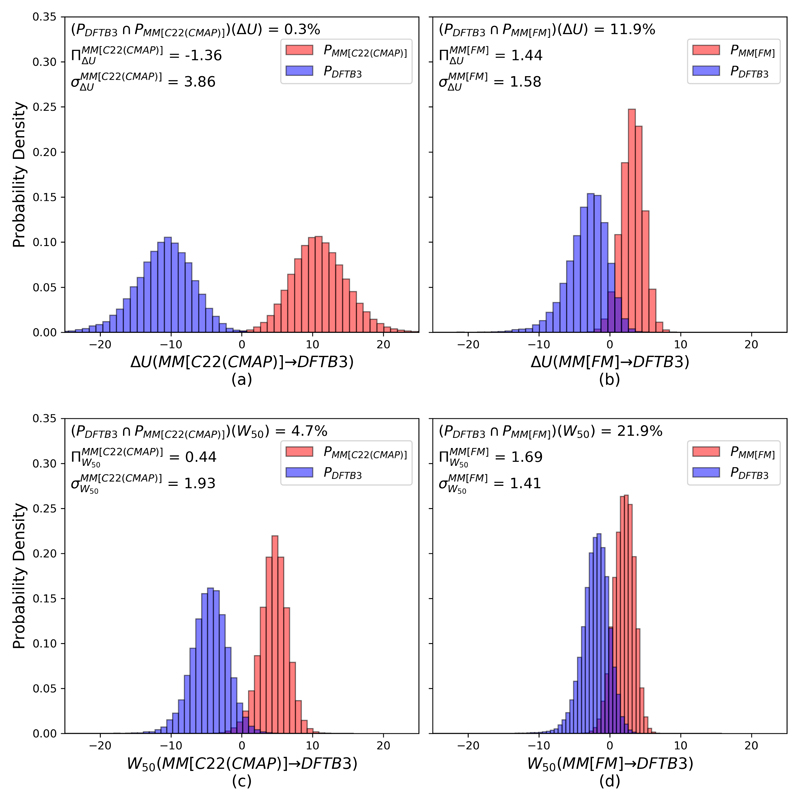
Calculating converged free energy corrections and correctly sampling backbone dihedrals for Ser offers a more challenging case for testing the MM[FM] procedure. From the P_low(ΔU^low→high) and P_high(‒ΔU^high→low) plots (Fig. 3) we see that the ΔU overlap between MM[C22(CMAP)] and DFTB3 is rather poor (0.3%, see Fig. 3a). Considering the rather large standard deviation of ΔU for MM[C22(CMAP)] $({\text{σ}}_{\text{Δ}U}^{\text{MM}[\text{C}22(\text{CMAP})]}=3.86\text{kcal/mol})$ in conjunction with the bias measure $({\displaystyle {\Pi }_{\Delta U}^{\text{MM}\left[\text{C}22\left(\text{CMAP}\right)\right]}=\text{-}1.36})$, we find that MM[C22(CMAP)]→DFTB3 completely fails the convergence criteria. Using MM[FM] as the low level of theory, overlap with DFTB3 increases significantly (11.9%, Fig. 3b). The associated standard deviation and bias measure of MM[FM] fall within satisfactory ranges $({\sigma }_{\text{Δ}U}^{\text{MM}[\text{FM}]}=1.58\text{kcal}/\text{mol}$ and ${\text{Π}}_{\text{Δ}U}^{\text{MM}[\text{FM}]}=1.44).$

Figure 3.

(a) Gas phase Ser potential energy difference histograms between the high level DFTB3 (P_DFTB3 configurations) and the MM[C22(CMAP)] (P_{MM[C22(CMAP)]} configurations) low level ensemble. (b) The same between the high level DFTB3 and the MM[FM] (P_MM[FM] configurations) low level ensemble. Each of the low level (e.g., P_{MM[C22(CMAP)]} and P_MM[FM]) histograms were generated using 100,000 configurational snapshots from 1 μs of LD, whereas the high level (e.g., P_DFTB3) was generated using 20,000 snapshots of 100 ns LD. (c) Gas phase Ser histograms of non-equilibrium work collected during 25 fs (50 step) fast switching W^{DFTB3→MM[C22(CMAP)]} simulations, started from coordinates and velocities generated at MM[C22(CMAP)] (100,000 snapshots) and DFTB3 (20,000 snapshots) levels of theory. (d) Non-equilibrium work histograms for W^{DFTB3→MM[FM]} simulations, starting from MM[FM] (100,000 snapshots) and DFTB3 (20,000 snapshots) configurations as the respective low and high levels of theory.

The plots in Figs. 3c and d show the effect of using the two low levels of theory (MM[C22(CMAP)] vs. MM[FF]) on the forward / backward distributions of non-equilibrium work values from short (25 fs) switching simulations (50 step with 0.5 fs time step, W₅₀). The combination of the MM[FM] approach with non-equilibrium work switches results in the highest overlap (21.4%, Fig. 3d). By comparison, using MM[C22(CMAP)] with the W₅₀ switching protocol yielded a significantly lower overlap of only 4.7% (Fig. 3c). The resulting free energy corrections ΔA^MM→DFTB3 for the two low levels of theory, using equilibrium and non-equilibrium techniques, are summarized in Table 1.

Table 1.

Results from various free energy methods to compute the MM to DFTB3 free energy correction for serine dipeptide in gas phase. All values are in units of kcal/mol, and ΔA^MM→DFTB3 values have been offset for clarity by +18, 500 and +19, 800 kcal/mol for MM[C22(CMAP)] and MM[FM], respectively). The columns labeled‘s’ represent the standard deviation estimate obtained from the aforementioned block averaging procedure (i.e., generating statistics by breaking data sets up into blocks of ten).

	ΔAMM→DFTB3
	MM[C22(CMAP)]	s	MM[FM]	s
FEPa	-45.22	0.25	-6.43	0.09
BARb	-46.65	0.12	-6.66	0.06
JAR50c	-46.82	0.19	-6.82	0.10
JAR100d	-46.62	0.16	-6.77	0.08
CRO50e	-46.66	0.09	-6.66	0.06
CRO100f	-46.67	0.08	-6.66	0.06

^aObtained using 100,000 MM snapshots

^bObtained using 100,000 MM snapshots and 20,000 DFTB3 snapshots

^cObtained using 100,000 MM→DFTB3 W₅₀ switching simulations

^dObtained using 100,000 MM→DFTB3 W₁₀₀ switching simulations

^eObtained using 100,000 MM→DFTB3 and 20,000 DFTB3→MM W₅₀ switching simulations

^fObtained using 100,000 MM→DFTB3 and 20,000 DFTB3→MM W₁₀₀ switching simulations

Remarkably, gauged against our overlap/convergence criteria the use of short non-equilibrium switches (W₅₀) between MM[C22(CMAP)] and DFTB3 performs worse than using MM[FM] and DFTB3 in combination with forward / backward energy differences (cf. Figs 3b and c). This strongly indicates that, although choosing a better one-sided method (e.g., JAR) can provide critical improvement when encountering poor overlap between levels of theory, selecting the “right” low level of theory will have an equally, if not stronger, influence. Further, the standard deviation of W₅₀ for MM[C22(CMAP)] $({\sigma }_{W_{50}}^{\text{MM}[\text{C}22(\text{CAMP})]}=1.93\text{kcal}/\text{mol})$ is almost half of ${\displaystyle {\sigma }_{\Delta U}^{\text{MM}\left[\text{C22}\left(\text{CMAP}\right)\right]}}$, but still falls just below the recommended bias measure threshold $({\Pi }_{W_{50}}^{\text{MM}[\text{C}22(\text{CMAP})]}=0.44<0.50).$ The standard deviation of W₅₀ for MM[FM] $({\sigma }_{W_{50}}^{FM}=1.41\text{kcal}/\text{mol})$ is slightly reduced, and the associated bias measure $({\text{Π}}_{W_{50}}^{FM}=1.69)$ is dramatically improved.

From these ΔU and W values, a variety of methods can be used to compute ΔA^MM→DFTB3 (e.g, FEP, JAR, BAR, and CRO). Reviewing the results for ΔA^MM→DFTB3 clearly reflects the expected failure of FEP to generate any meaningful result (off by about 2.5k_BT) when choosing MM[C22(CMAP)] as the MM level of theory. Somewhat surprisingly, the FEP results using MM[FM] are possibly adequate, falling within 0.5k_BT of the true result. Results obtained with JAR50 and JAR100 (50/100 step switches with 0.5 fs timestep), although similar in accuracy, differ significantly in standard deviation and thus again point to the MM[FM] result as the more reliable of the two. Results obtained with BAR demonstrate strong agreement to those found for the CRO50 and CRO100 switches, though the BAR result for MM[C22(CMAP)] clearly has a larger standard deviation.

To demonstrate the effectiveness of the intramolecular FM procedure in correcting “soft” degrees of freedom, we re-examine the problematic Ser dihedrals (Fig. S1), as previously demonstrated in Ref.33. Looking at the ϕ, ψ (Fig. S2a) and χ₁ (Fig. S2b) plots, we see that the mismatch between MM[C22(CMAP)] and DFTB3 is fairly dramatic, with MM[C22(CMAP)] having a global conformational minimum around (ϕ, ψ, χ₁)=(-160°, 165°, -170°) versus DFTB3 with the minimum at (ϕ, χ, χ₁)=(-80°, 80°, 55°). The MM[FM] generated plots, on the other hand, show both conformational minima of interest, and, thus, appreciably more configurational overlap with DFTB3 is expected.

Conclusions

In this study, we described the development and implementation of a straightforward procedure for “improving” classical force field parameters. This FM based procedure utilizes QM or SQM forces as the target to produce a modified classical force field (e.g., CHARMM topology and parameters). This new FM technique was applied to two test cases that are representative of the problems associated with efficiently and effectively utilizing the indirect thermodynamic cycle for QM/MM free energy simulations; i.e., converging free energy simulations between “low” (i.e., classical, MM) and “high” (i.e., quantum, QM) levels of theory (i.e., ΔA^MM→QM).

The results from these initial, proof-of-concept, test cases clearly establish the usefulness of FM techniques for enhancing conformational overlap between levels of theory. Even though high level probabilities and energetics were not perfectly captured, the MM[FM] ensemble significantly improved sampling in the relevant regions of DFTB3’s conformational space. Further, the improved accuracy and precision of the MM[FM] parameters increased the efficiency of reweighting techniques (e.g., NBB²⁸) and possibly make FEP a viable option. Ultimately, the combination of MM[FM] with non-equilibrium work techniques appears to be a very promising and robust approach.

Take note, in most practical applications of FM approaches, parameter transferability is abandoned. This means that, as demonstrated with the gas-phase test cases presented, FM can allow for better reproduction of gas phase dynamics. However, this does not necessarily mean that gas phase FM parameters would be appropriate for all situations (i.e., reproducing condensed phase properties). This is exemplified in the discussion of Ref. 42, where it was noted that in order to properly model solution phase properties, the gas phase description deteriorated. Questions of best practice regarding how well FM parameters perform in changing environments will be addressed in a follow up publication.

Supplementary Material

The following can be found in the supporting information: A diagram of the relevant “soft” degrees of freedoms for serine dipeptide; probability distributions for the relevant Ser ϕ, φ and χ₁ angles; examples of ΔU overlap and standard deviation; details on the intramolecular fitting form; git repository location for the latest forcesolve version; discussion of expressing dihedral terms as a linear function; an explanation of the FM likelihood derivation utilized in the forcesolve software; details of the training set; a copy of the forcesolve software utilized in the calculations demonstrated in the manuscript; a scheme illustrating the work flow of implemented; a table of force RMSD before and after FM for both Ser and butane; self contained copies of the CHARMM parameters used (MM[CGenFF] for butane, MM[C22(CMAP)] for Ser) and the MM[FM] parameter sets for both test cases.