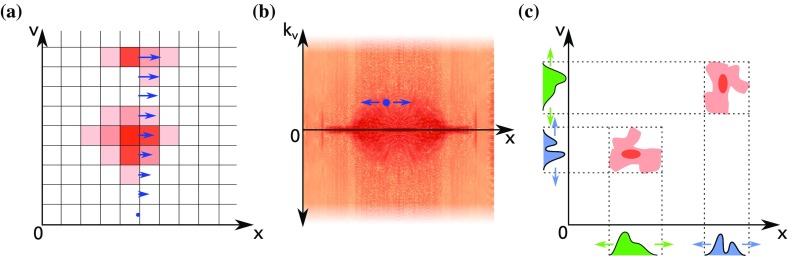
Fig. 2.

Different ways of numerically representing the phase-space density $f(\mathbf{x},\mathbf{v},t)$: a In a Eulerian grid, every grid cell stores the local value of phase-space density, which is transported across cell boundaries. b Spectral representations (shown here: Fourier-space in $\mathbf{v}$) allow for some update steps of phase-space density to be performed locally. c In a tensor train representation, phase-space density is represented as a sum of tensor products of single coordinates’ distribution functions which get transported individually